Space and Time
공간 안에서 시간을 소요하며 최적화된 결과를 찾는다.

Space Complexity
공간은 problem (state) space 와 search (solution) space 로 구성된다.
Problem (state) space
답을 찾기 위한 정해진 공간을 problem space 라고 한다.
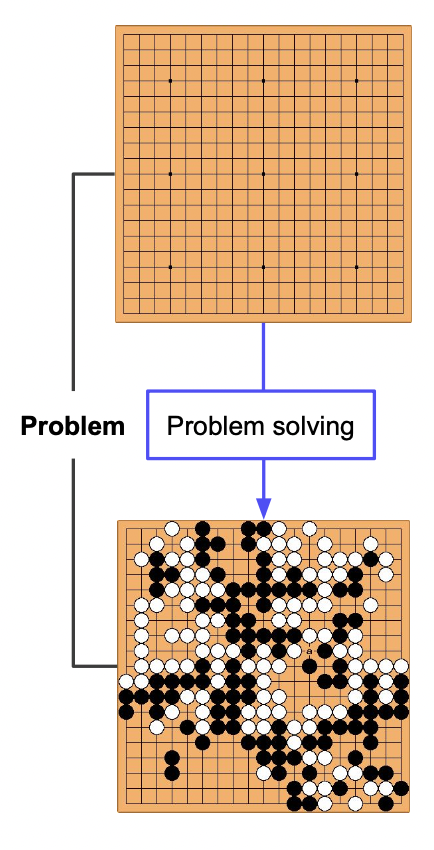
아래의 예시에서는 바둑판 모양의 행렬이 해당된다.
Search (solution) space
답을 찾는 과정에서 답의 가능성이 있는 모든 집단을 search space 라고 한다.
바둑 예시에서 이기기 위한 과정 중 모든 중간 결과들이 해당된다.
Time Complexity
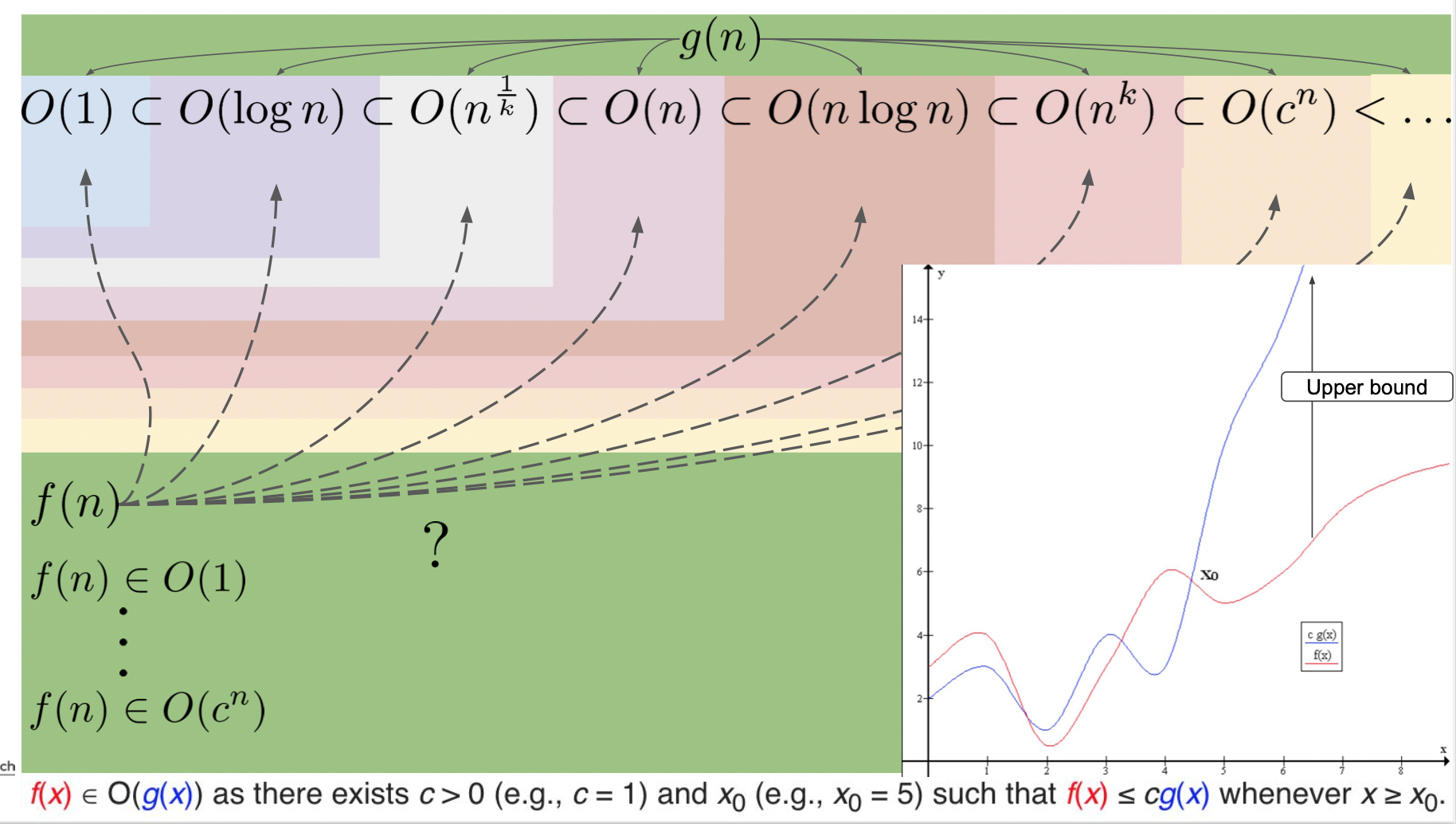
답을 찾기 위해 반복 수행되는 대략적인 시간을 의미한다. 표현은 주로 upper bound, 최대 시간을 측정하기 위해 빅오 O() 로 나타내며 아래와 같이 시간의 크기를 생각해볼 수 있다.
Time-space Trade-off
답을 찾아나갈 때, 시간을 더 쓰는 대신 공간을 절약하거나 공간을 더 쓰는 대신 시간을 절약하는 trade-off 가 있을 수 있다.
Entropy
무질서도
entropy 가 커진다는 것은 시간의 흐름에 따라 경우의 수가 많아지는 것을 뜻한다.
참고로 우주의 엔트로피는 증가하고 있다.
비유하자면 정리된 방 (과거) 에 아기를 두면 자연적으로 어질러질 것 (미래) 이다.
시간에 따라 엔트로피가 커지는 것이다.
에너지를 들여서 방을 정리하면 엔트로피가 감소하며 미래에서 과거로 간다고 볼 수 있다.
Information entropy
어떠한 정보를 얻기 위해 몇 번의 질문을 해야하는지로 생각해볼 수 있다.
한 정보를 얻을 확률 x 로 정보를 얻기 위해 필요한 질문의 수를 모든 정보에 대해 수행하고 더하면 entropy 가 된다.
문제를 풀 때, 어질러진 상태 (랜덤 웨이트) 에 에너지를 들여 원하는 최적화된 상태로 바꾸는 것을 말한다.
참조
https://hyunw.kim/blog/2017/10/14/Entropy.html
Parameter Search
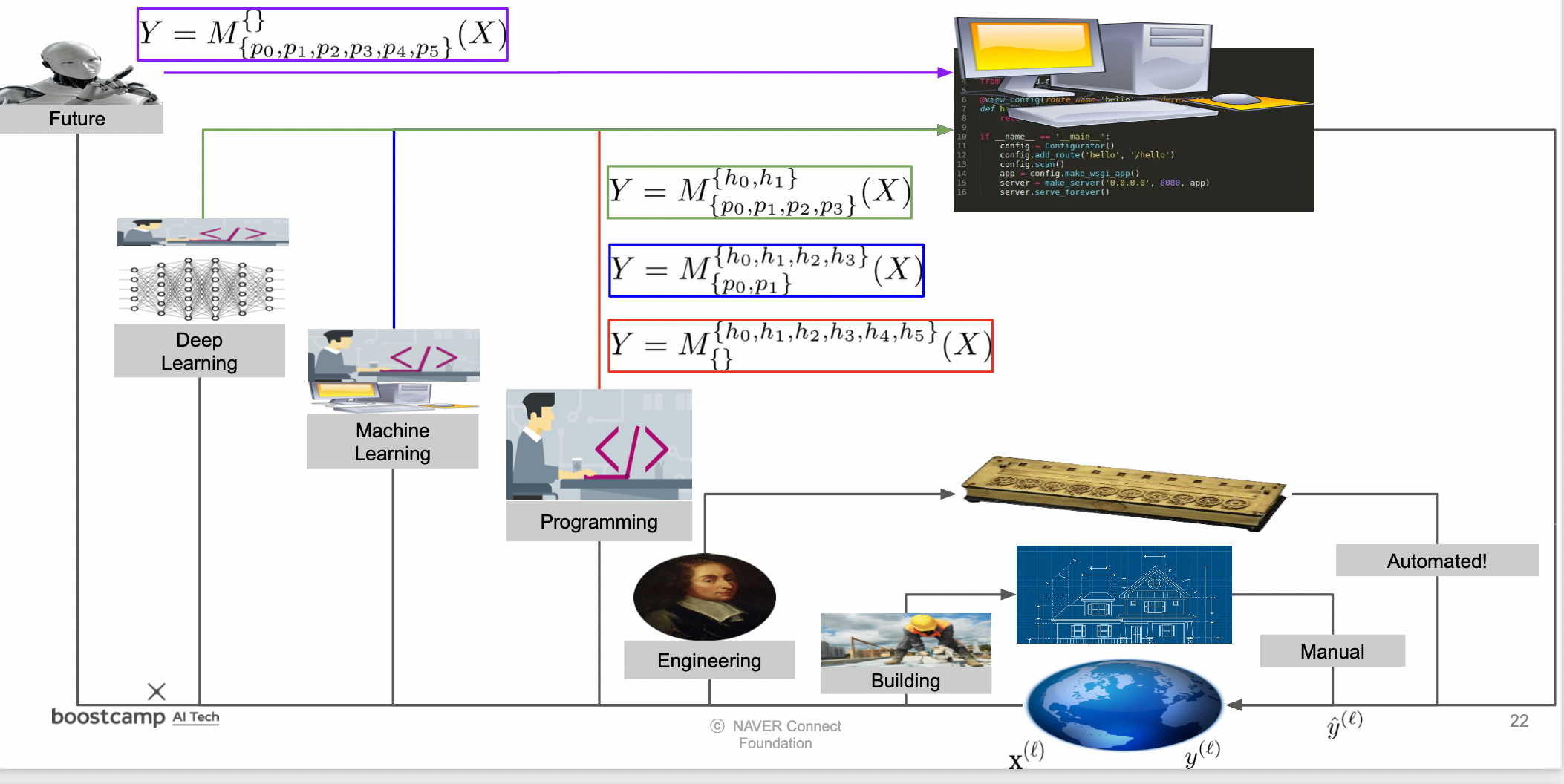
어떤 답을 찾는 모델을 만들기 위해서는 1) architecture 를 먼저 구성하고 다음으로 2) 고정된 hyperparameter 를 찾고 마지막으로 3) parameter 를 수정해야 한다.
예전에는 사람이 모든 parameter 를 찾았지만 시간이 갈 수록 기계가 모든 parameter 를 찾아주고 있다.
딥러닝 적용
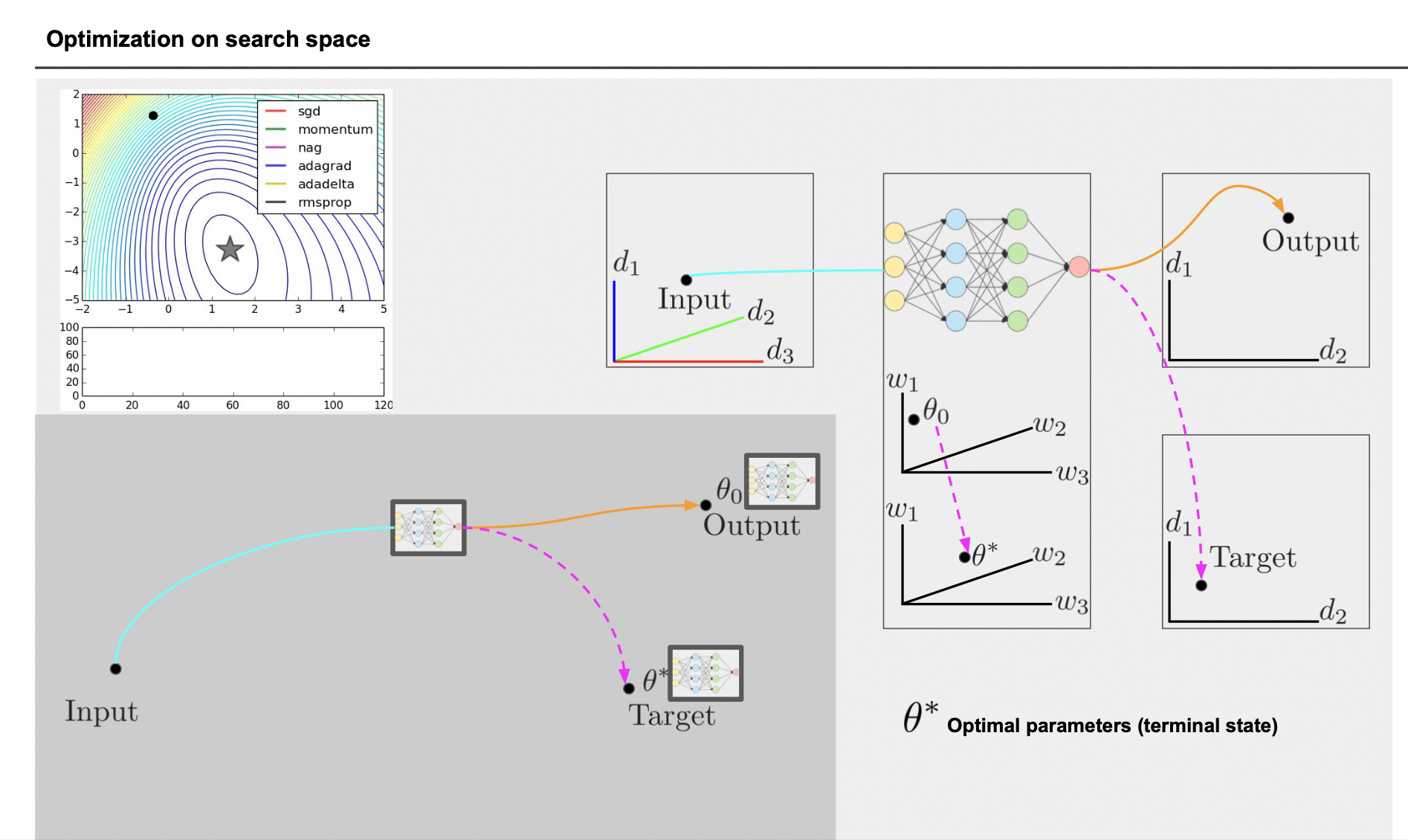
입력, 중간 레이어, 결과 모두 다차원 공간 속의 점이다.
딥러닝에서는 귀납적으로 최적의 결과를 나타내기 위해 중간 레이어의 parameter 를 수정해나간다.
Hyperparameter Search
Batch 사이즈, 이미지 종류, 레이어 depth 등 정답을 찾기 위해 미리 설정하는 변수를 hyperparameter 라고 한다.
hyperparameter 는 조금만 바뀌어도 모델이 큰 영향을 받으므로 적절한 hyperparameter 를 찾는 것은 중요하다.
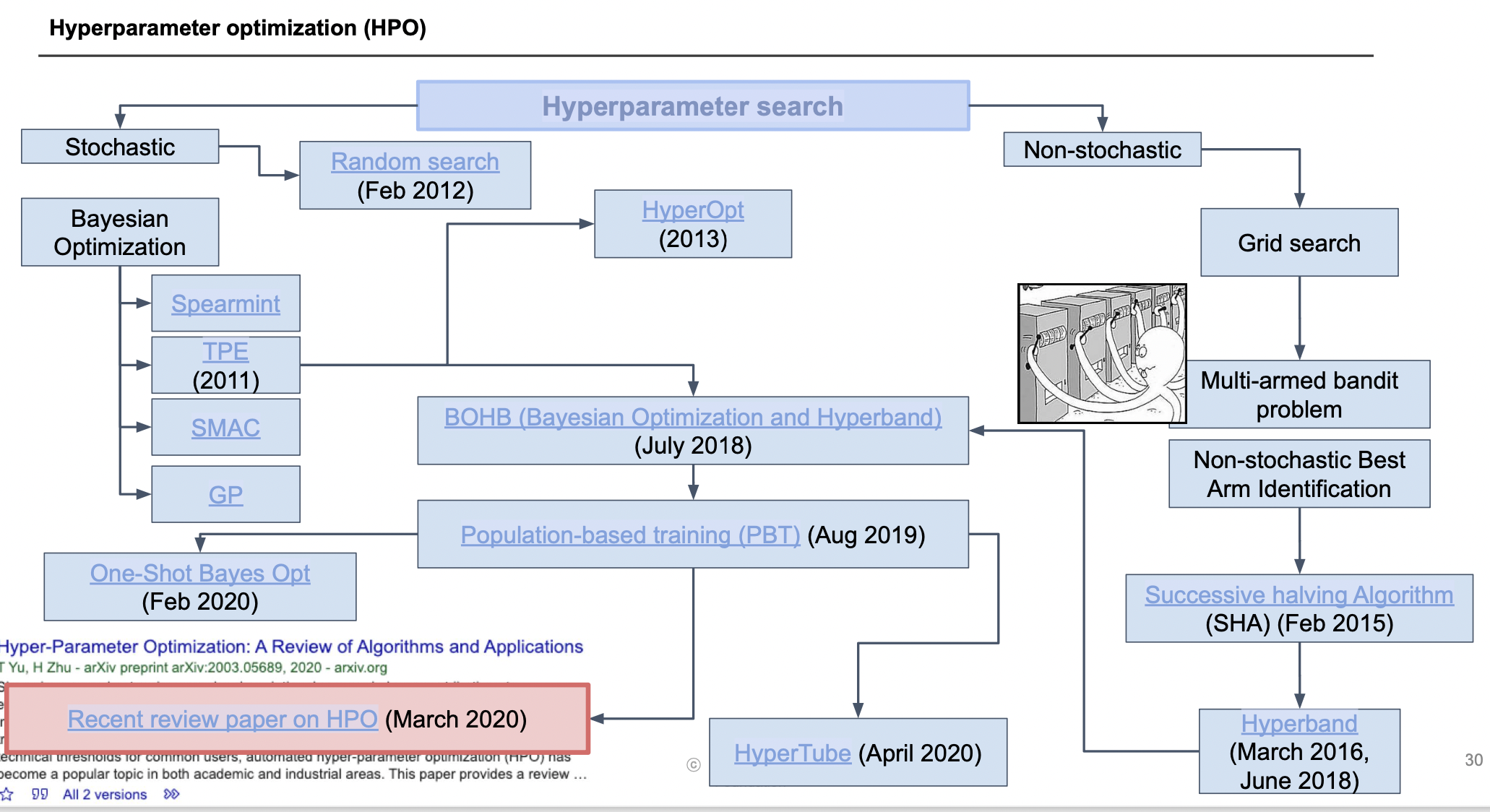
hyperparameter 최적화 논문들
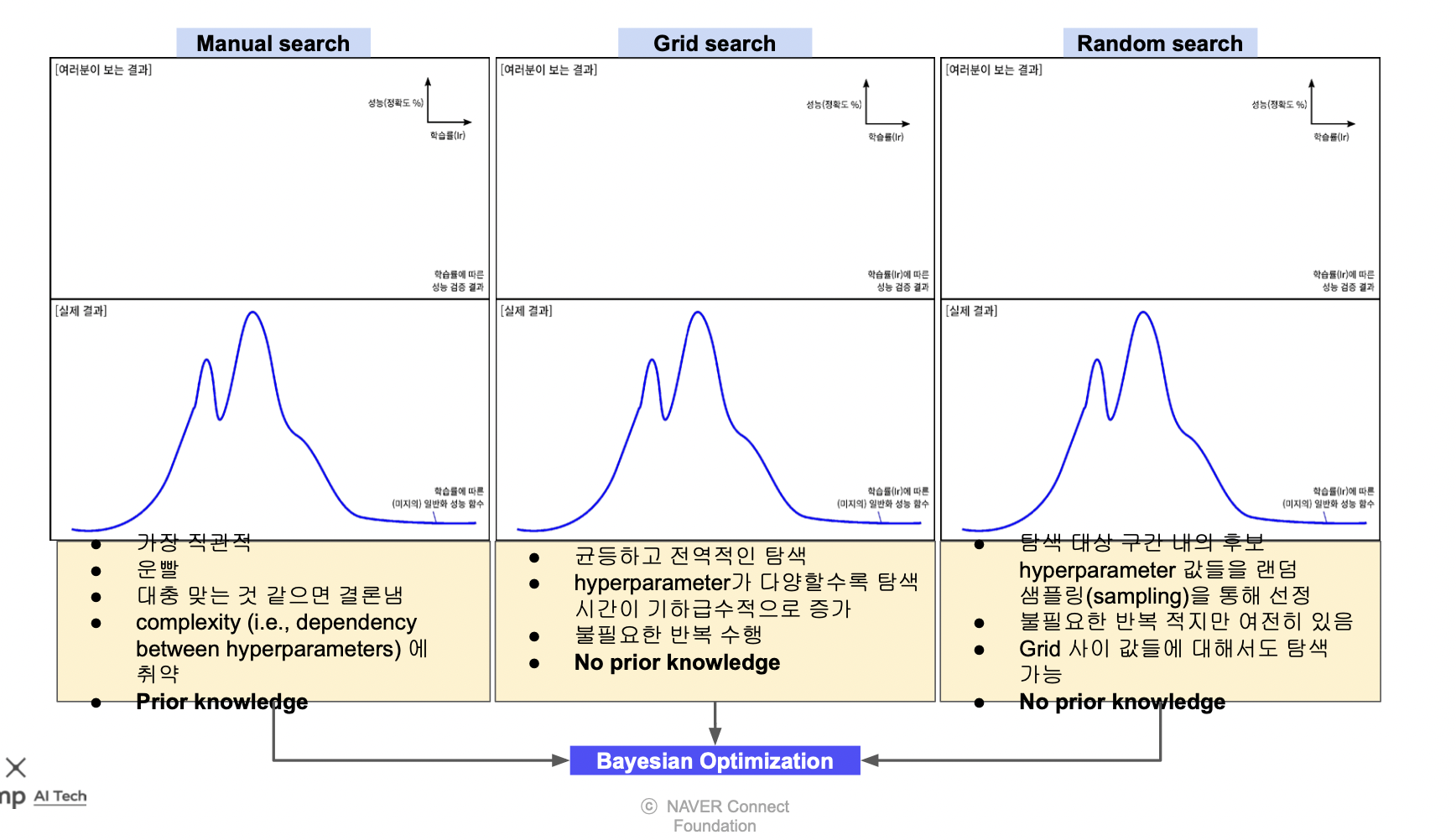
Manual vs Grid vs Random search
Gaussian process (서로게이트 모델)
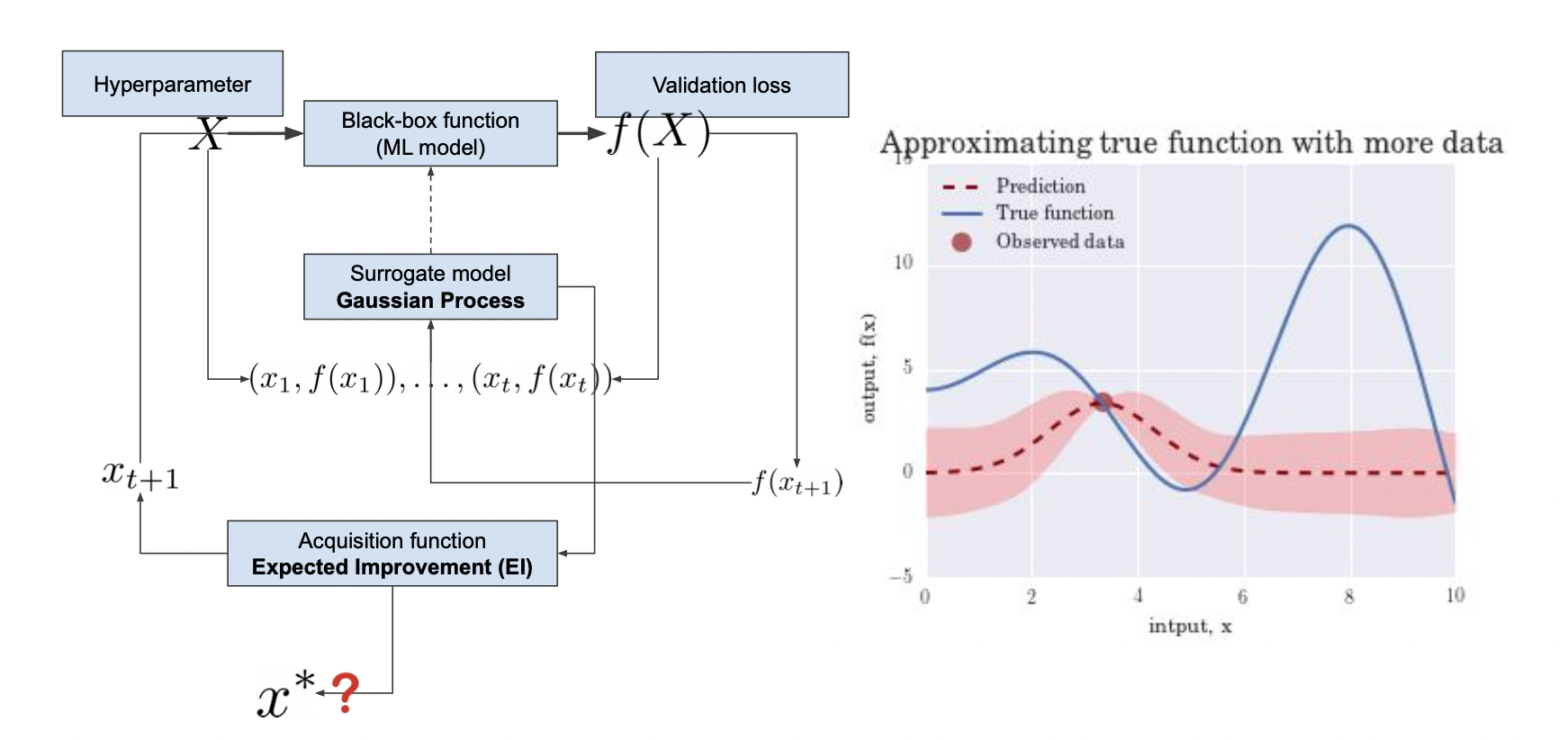
일반적으로 Cross-validation 을 통해 hyperparameter 를 튜닝하는데 validation loss 가 나오면 평균과 분산을 이용하는 Gaussian process 로 수정하는 방법이 있다.
이는 전체 모델을 돌리는게 아니므로 큰 비용이 들지 않는다.
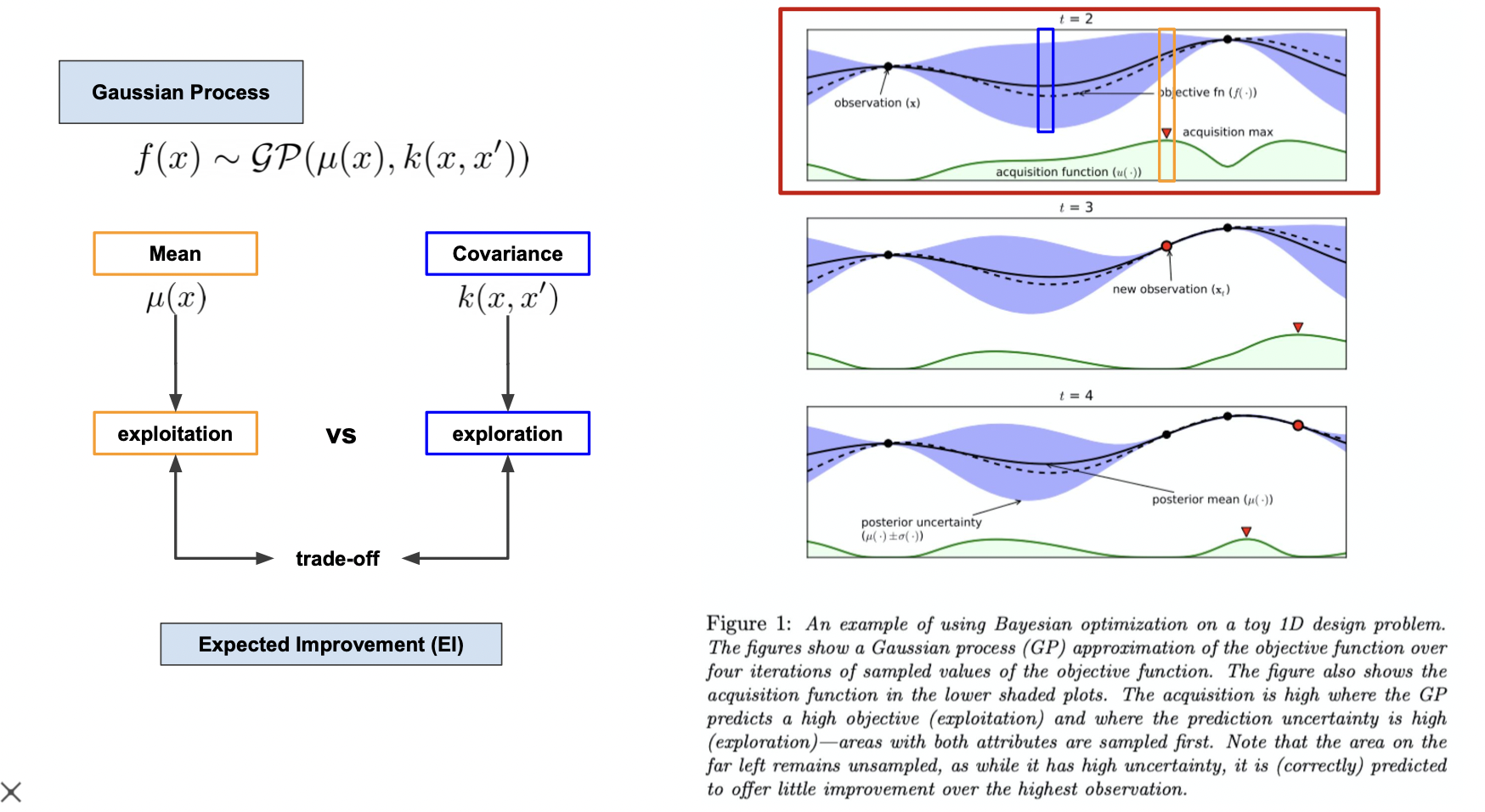
베이즈 정리를 이용하여 사전 확률을 관측 값 (점) 을 통해 사후 확률로 바꾸는 과정을 반복하며 하이퍼 파라미터를 찾는다.
평균과 분산은 trade-off 관계이기 때문에 acquisition 함수가 가장 높은 지점을 관측값으로 잡는다.
Neural Architecture Search
가장 토대가 되는 architecture 를 어떤 모델을 쓸지 찾아야 한다.
Manual 하게 찾거나 automatic 하게 찾을 수 있다.
목적에 따라 모델은 달라진다.
multi-objective NAS (원하는 여러 목적을 만족하는) 를 찾는 과정은 네트워크 압축과 비슷하다.
반대로는 압축 과정이 NAS 와 비슷하다고 할 수 있다.
Automatic NAS
모델을 세팅하고 돌려서 결과를 보며 적절한 모델을 찾는다.
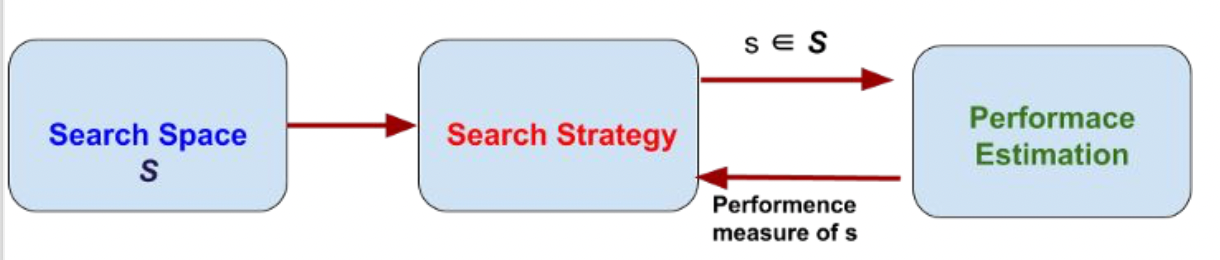
NAS for Edge Devices
엣지 디바이스에 사용되는 NAS 방법으로는 아래의 방법들이 있다.
MnasNet
스마트폰에서 사용하기 적절한 모델이다.
https://arxiv.org/pdf/1807.11626.pdf
논문을 통해 본 모델에 대해 자세히 살펴볼 수 있다.
ProxylessNAS
원래는 프록시 (대리로 흉내) 로 경량화를 했는데 프록시를 쓰면 실제와 맞지 않는 경우가 있어서 프록시를 사용하지 않고 모델을 구현하였다.
https://arxiv.org/pdf/1812.00332.pdf%C3%AF%C2%BC%E2%80%B0
Once-for-all
네트워크를 한 번 트레이닝 시켜서 여기 저기 적용할 수 있게 만든 모델이다.
https://arxiv.org/pdf/1908.09791.pdf
MobileNet 시리즈
아래의 세가지 방법을 적용한 모델이다.

Regular convolution vs Depth-wise Separable convolution
1x1 conv 를 사용한 후자가 파라미터와 계산량을 줄여서 더 좋다.
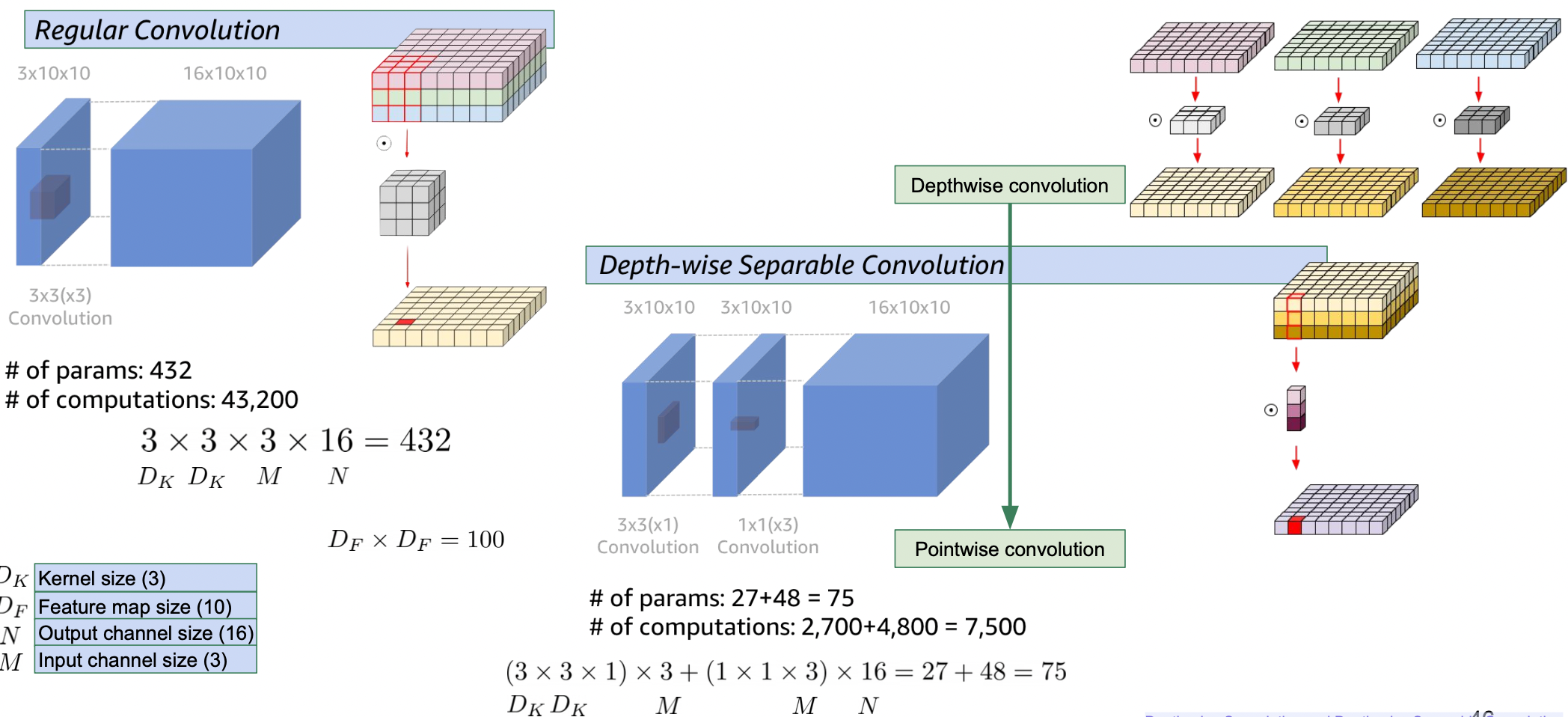
https://arxiv.org/abs/1704.04861
참조
BoostCamp AI Tech
