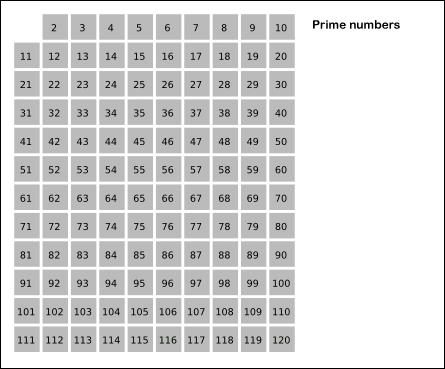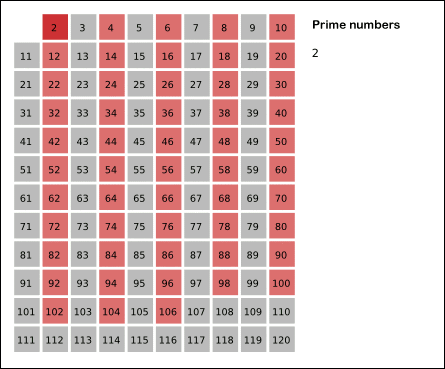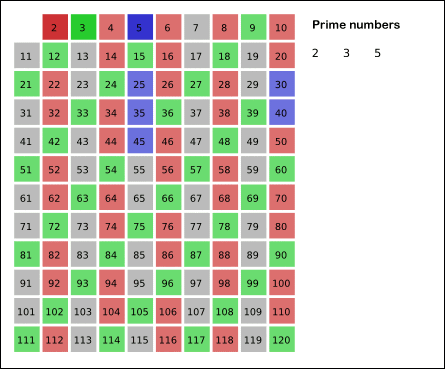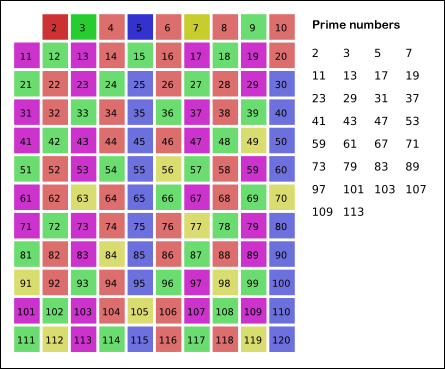
✔ 풀이를 위한 아이디어
- 에라토스테네스의 체 (Eratosthenes Sieve)
✔ 수정 전 코드 [메모리 초과]
import sys
N, M = map(int, sys.stdin.readline().split())
nums = [1]*M
i = 2
while i**2 <= M: # i<=M보다 효율적이며, 이렇게만 해도 충분하다
j = i**2
while j <= M:
nums[j-1] = 0
j = j + i**2 # 이렇게 하나씩 더해줌으로써 4, 8, 12..
i += 1
count = M-N+1
for i in range(N, M+1):
if nums[i-1] == 0:
count -= 1
print(count)- 이전에 풀었던 백준 1978번 문제 (소수 찾기) 를 조금만 바꿔서 제출하였다. 에라토스테네스의 체는 큰 범위에 있는 소수들을 효율적으로 찾아낼 때 매우 효율적인 알고리즘이다. 하나의 수가 소수인지 판정하기 위해서는 https://myjamong.tistory.com/139 의 링크에 나와있는 것과 같이 코드를 작성하지만, 큰 범위에서 각각의 수들에 모두 이 방식을 사용하면 시간복잡도가 심각하게 높아지게 되므로 에라토스테네스의 체를 활용하는 것이 필수적이다.
- 하지만 위의 코드는 N부터 M까지만 판별한 것이 아니라, 1부터 M까지를 다 판별한 후에 값을 셀 때만 N부터 했으므로 nums라는 배열이 너무 큰 메모리를 차지하게 되어 오답으로 처리되었다.
✔ 수정 전 코드 [시간 초과]
import sys
N, M = map(int, sys.stdin.readline().split())
nums = [1]*(M-N+1) # 필요한 사이즈 만큼만 nums 생성
i = 2
while i**2 <= M:
j = i**2
while j < N: # 나누는 수가 최솟값보다 커질 때까지 while문 돌리기
j += i**2
while j <= M:
nums[j-N] = 0
j += i**2
i += 1
count = len(nums)
for i in range(M-N+1):
if nums[i] == 0:
count -= 1
print(count)- 따라서, 필요한 사이즈인 M-N+1 만큼만 nums를 선언하고, N보다 크거나 같은 j에 대해서만 nums의 값들을 바꿔주도록 하였다.
- 그러나, 나누는 수가 최솟값보다 커질 때까지 저런식으로 while문을 돌리게 되면 N의 값이 커질 수록 시간복잡도가 매우 높아지게 되고, 결과적으로 시간초과를 받게 되었다.
✔ 수정 후 코드
import sys
import math
N, M = map(int, sys.stdin.readline().split())
nums = [1]*(M-N+1)
i = 2
while i**2 <= M:
j = math.ceil(N / i**2) * (i**2) # while문을 돌리지 않고 그냥 한번에 구해버리기
while j <= M:
nums[j-N] = 0
j += i**2
i += 1
print(sum(nums)) # 이 부분은 바꾸지 않아도 되긴 하는데, 이렇게 처리하면 좀 더 깔끔- while문을 돌리지 않고 한번에 j 값을 구해내는 방법을 떠올리기가 사실 되게 어려웠다.
- 하지만 예를 들어서 생각해보면 간단하다. 예를 들어 i가 2이고 N이 101이라면,
i^2인 4로 나누어떨어지면서, 101보다 큰 최소의 수인 j는 26 x 4 인 104가 될 것이다. - 이를 구하기 위해서 N 값을 i^2로 나눠주고, 이를 올림 (math.ceil() 모듈 활용) 처리 해주면 위의 예시에서 26과 같은 값을 얻어낼 수가 있다.
- 얻어진 값에 다시 i^2을 곱하면 우리가 원하는 최소의 j 값을 한번에 구할 수 있게 된다.
- 이렇게 처리하고 나니, 시간초과 문제가 더이상 발생하지 않았다.

✔ 관련 개념
- 에라토스테네스의 체 (Eratosthenes Sieve) 의 효율적 활용