Problem Solving
1.백준 1018번: 체스판 다시 칠하기
✔ 풀이를 위한 아이디어메모리 초과를 방지하기 위해 input() 대신 sys.stdin.readline() 사용8x8짜리 부분집합이 (N-7)\*(M-7)개 나온다는 사실좌표의 합이 짝수인지 홀수인지 살펴보면 체스판처럼 색을 칠할 수 있다는 생각2차원 배열을 x, y
2.백준 1181번: 단어 정렬
✔ 풀이를 위한 아이디어비어 있는 이차원 배열 만들기 (더 효율적인 방법이 있다면 수정하면 좋을 것 같다)처음부터 애초에 글자수에 따라 분류해서 저장하고, 같은 글자수 안에서만 정렬과 중복제거가 일어나도록 설계✔ 코드
3.백준 1654번: 랜선 자르기
✔ 풀이를 위한 아이디어이분탐색 (Binary Search) 의 활용✔ 수정 전 코드기존에 가지고 있던 랜선을 잘라서 만드는 것이기 때문에, 구하려는 정답은 가지고 있던 랜선들 중 가장 작은 값보다 커질 수 없다고 생각했다. 그러나 기존에 가지고 있던 랜선 중 하나를
4.백준 1874: 스택 수열
✔ 풀이를 위한 아이디어직접 push/pop 하지 않고 index로 접근하기✔ 코드미리 n개의 숫자를 배열에 넣어둔 뒤에, current_index라는 변수만 왔다갔다 하면서 push와 pop의 기능을 대신하도록 짜보았다.이때, pop으로 인해 없는 것으로 간주되어야
5.백준 1920: 수 찾기
✔ 풀이를 위한 아이디어이분탐색 (Binary Search) 의 활용 (복습)✔ 코드리스트 A를 sorted 함수를 활용해 정렬한 뒤, Q에 있는 요소들을 하나씩 이분탐색 해나가면 풀리는 간단한 문제이다.정렬 알고리즘 대신 sorted 함수를 사용하고, 1씩 증가시키며
6.백준 2108번: 통계학
✔ 풀이를 위한 아이디어collections 모듈의 Counter 클래스 활용 ✔ 코드최빈값을 구하는 것 외에는 매우 쉬운 난이도의 문제였다.for문을 활용해 최빈값을 구할 수도 있지만, 좀 더 효율적인 모듈이 없을까 하여 찾아보니 위와 같은 방법이 있었다.Counte
7.백준 2231번: 분해합
✔ 풀이를 위한 아이디어각 자리수의 합이 최대 얼마나 될 수 있는지 계산해서 탐색의 범위 좁히기✔ 코드사실 내가 설정한 탐색의 범위가 가장 효율적이라고 할 수는 없다. 최대의 효율로 탐색하려면 자릿수에 따라 범위를 나누되, 18 이하의 수들에 한에서 또 다른 범위를 설
8.백준 2609번: 최대공약수와 최소공배수
✔ 풀이를 위한 아이디어유클리드 호제법 (Euclidean-algorithm)최소공배수 = 두 자연수의 곱 / 최대공약수✔ 코드두 자연수의 최대공약수를 구하는 가장 일반적인 방법은 소인수분해를 통해 공통의 인수를 찾는 것이다. 그러나 이는 숫자가 커지게 되면 비효율적이
9.백준 9012번: 괄호
✔ 풀이를 위한 아이디어스택(Stack) 구조의 이해와 이를 바탕으로 한 효율적인 코드 작성✔ 코드스택(Stack)을 활용하여 문제를 푸는 것은 맞지만, 실제로 스택 구조를 구현하지는 않고 left라는 변수에 '('의 개수를 추가해주는 식으로 작성하였다. (push하는
10.백준 2164번: 카드2
✔ 풀이를 위한 아이디어덱(deque) 모듈의 사용✔ 코드처음에는, 배열에 요소가 딱 1개 남을 때까지 계속해서 홀수번째에 있는 요소들 (index = 0, 2, 4..)을 지워나가는 방법을 생각했다. 그러나 이 방법으로는 시간복잡도를 줄일 수 없었다.결국 구글링을
11.백준 11866번: 요세푸스 문제 0
✔ 풀이를 위한 아이디어원형 큐(Circular Queue)에서의 index 관리와 요소의 삭제✔ 코드직접 queue를 구현하지는 않고, counter라는 리스트를 통해 해당 index의 요소가 남아있는지, 남아있지 않은지 판별하였다.복잡한 while문과 for문을 사
12.백준 10816번: 숫자 카드 2
✔ 풀이를 위한 아이디어collections 모듈의 Counter 클래스 활용이분탐색 (Binary Search) 의 활용✔ 코드Counter 클래스의 most_common() 메쏘드까지 사용하고 나면, 등장 횟수를 기준으로 내림차순으로 정렬된다. 하지만 이분탐색을 하
13.백준 5430번: AC
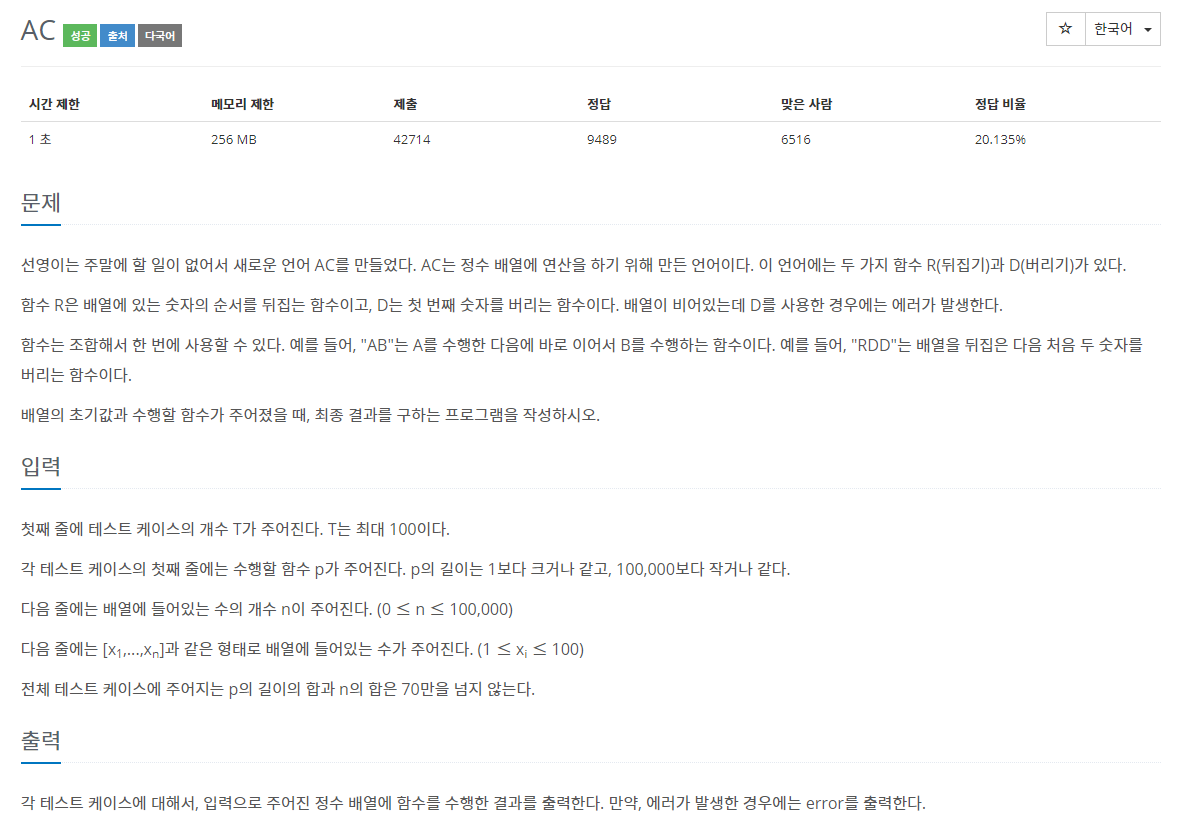
✔ 풀이를 위한 아이디어문자열(string)에서 필요한 요소 뽑아내기덱(deque)을 직접 구현하지 않고 index로 관리하기✔ 코드1,2,3,4와 같은 형식의 입력값에서 숫자들을 추출해 배열로 만들어야하므로 for문을 돌며 경계값을 감지해 nums라는 배열에 추가해줬
14.백준 1463: 1로 만들기
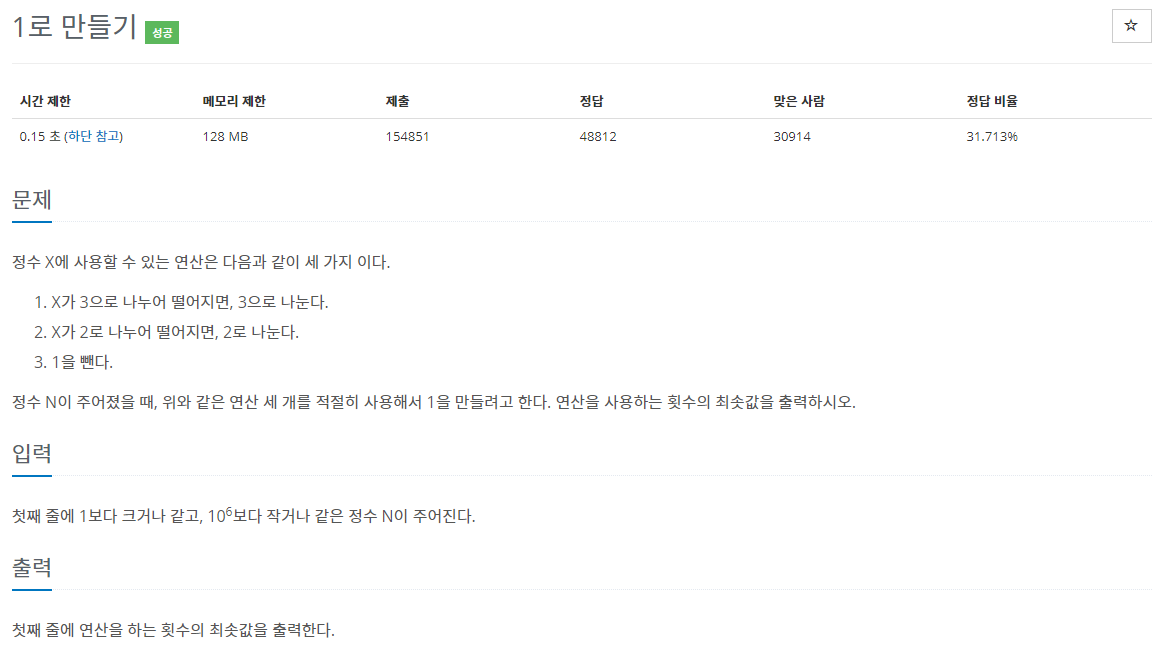
✔ 풀이를 위한 아이디어동적 프로그래밍 (Dynamic Programming)✔ 수정 전 코드처음에는 그리디 알고리즘(Greedy Algorithm)을 통해 구현할 수 있을 것이라고 생각했다. 그래서 다양한 케이스들을 직접 테스트 해보며 나름 완벽하다고 예상되게 코드를
15.백준 1260번: DFS와 BFS
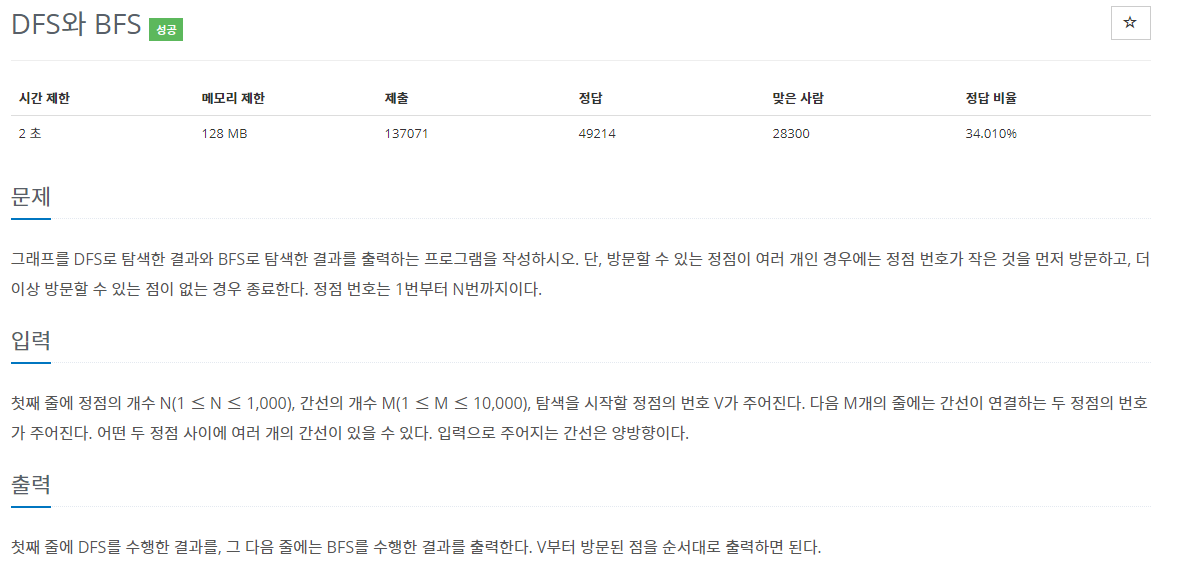
✔ 풀이를 위한 아이디어 그래프 (Graph) 이론 깊이 우선 탐색 (DFS) 과 너비 우선 탐색 (BFS) ✔ 코드 ~ [1,2,3,4]와 같은 형식의 입력값에서 숫자들을 추출해 배열로 만들어야하므로 for문을 돌며 경계값을 감지해 nums라는 배열에 추가해줬다
16.백준 7576번: 토마토
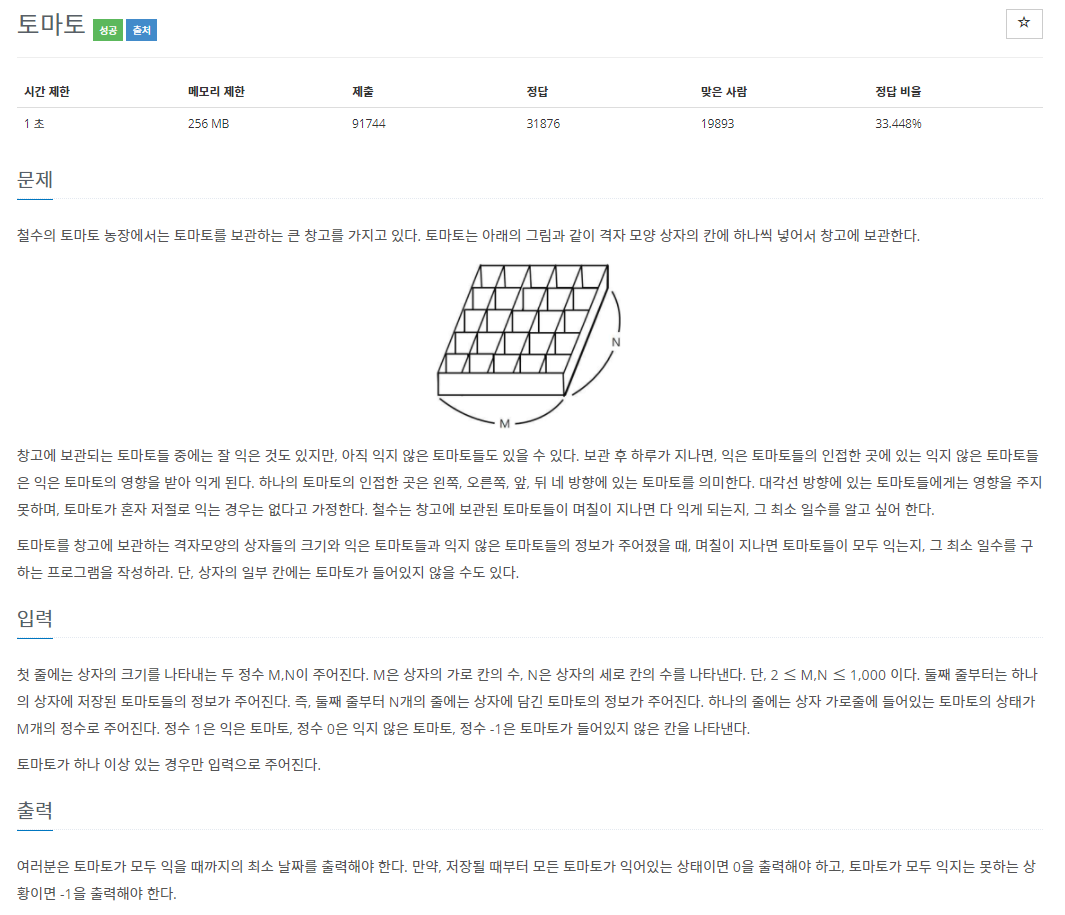
✔ 풀이를 위한 아이디어그래프 (Graph) 이론너비 우선 탐색 (BFS)✔ 코드바로 인접한 토마토부터 차례차례 익기 때문에 큐 (Queue)를 사용하는 너비 우선 탐색 (BFS)을 하였다. 이때, 연산의 최소화를 위해 덱 (Deque) 모듈을 사용하였다.기본적인 BF
17.백준 1012번: 유기농 배추
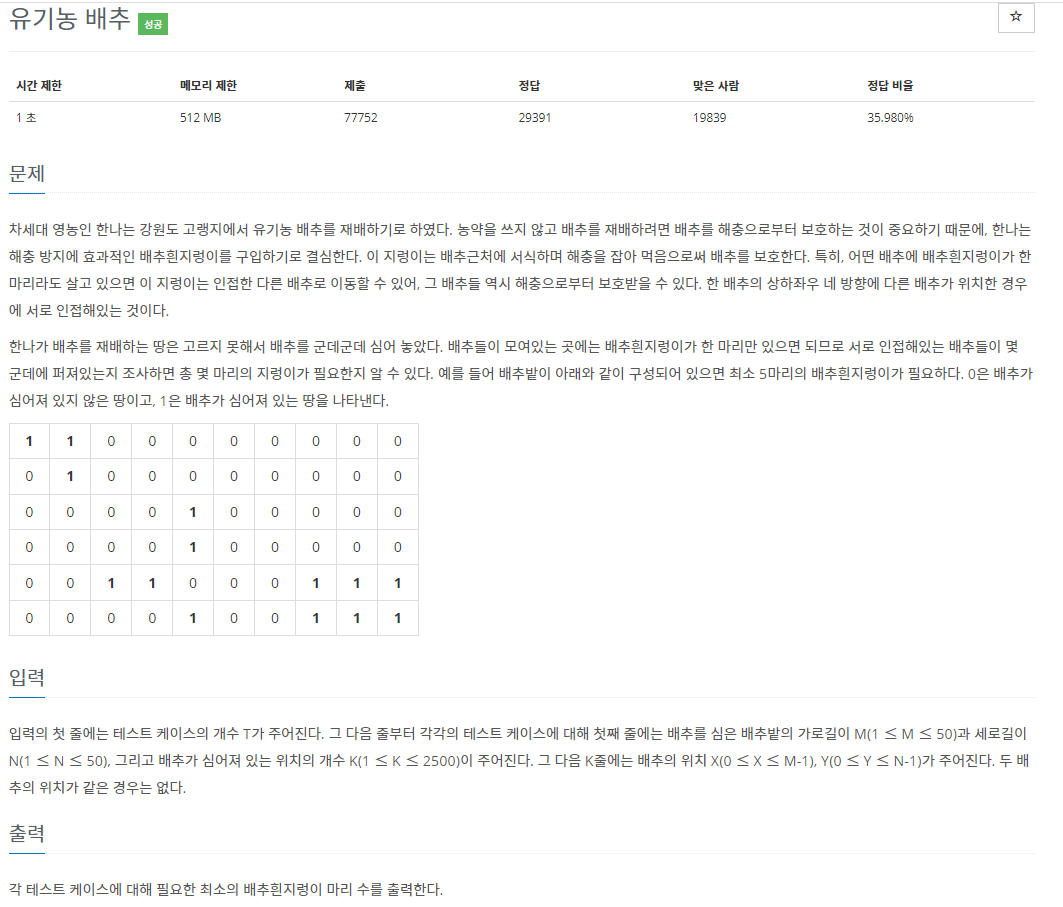
✔ 풀이를 위한 아이디어그래프 (Graph) 이론깊이 우선 탐색 (DFS) 과 너비 우선 탐색 (BFS)✔ 코드이전에 풀었던 토마토 문제에서 좀만 더 생각하면 쉽게 풀 수 있다.토마토 문제에서는 익은 토마토가 끊임 없이 주변 토마토를 익게 하기 때문에 맨 처음에 익어
18.백준 11399번: ATM
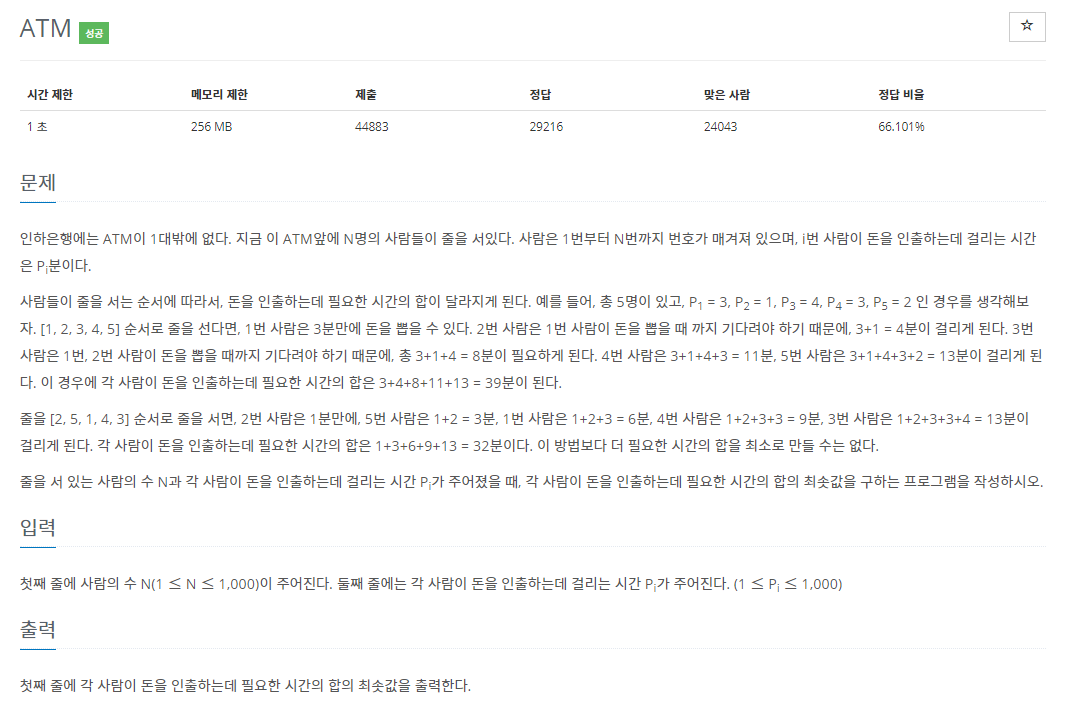
✔ 풀이를 위한 아이디어그리디 알고리즘 (Greedy Algorithm) 과 정렬 (Sorting)정말정말 간단한 문제인데, 너무 어렵게 생각했어서 반성하고자 글로 남긴다.✔ 코드처음 이 문제를 접했을 때, N명을 일렬로 세우는 모든 경우의 수를 고려하고 그 중에서 최
19.백준 1697번: 숨바꼭질
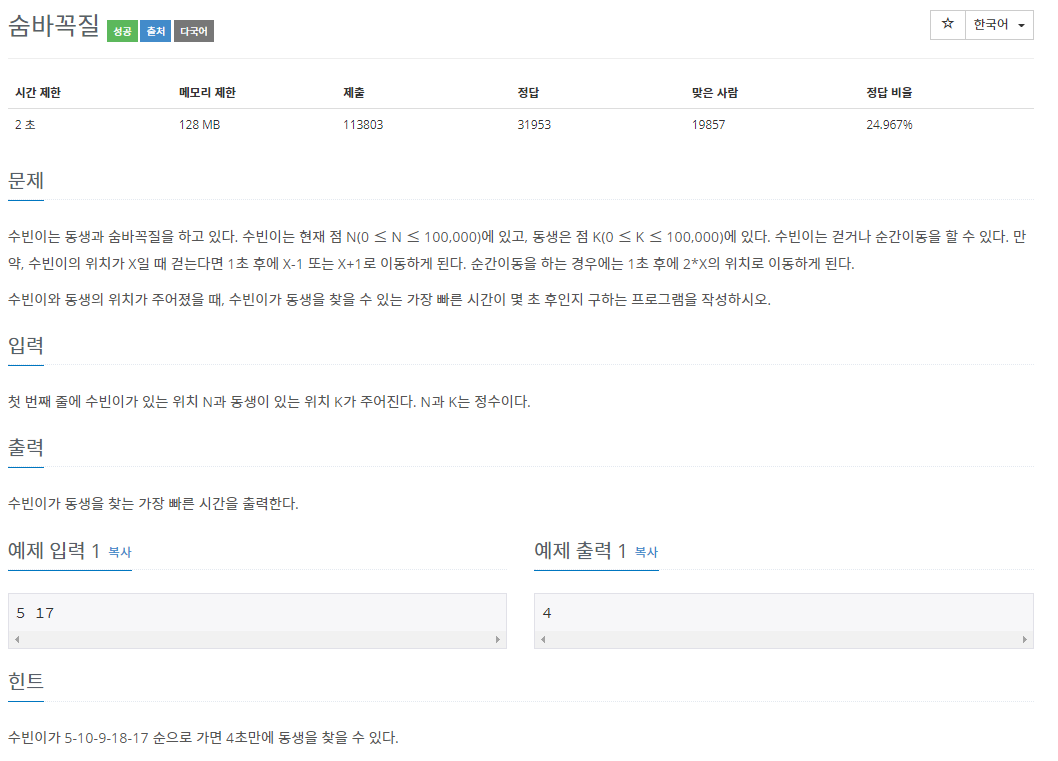
✔ 풀이를 위한 아이디어그래프 (Graph) 이론과 너비 우선 탐색 (BFS)메모리 초과와 시간 초과 방지하기✔ 수정 전 코드 1 메모리 초과사실 풀이의 방향성은 맞았다. BFS를 활용하여 N-1, N+1, 2\*N의 3가지 갈래로 계속해서 뻗어나가고, 그러다가 찾는
20.백준 11279번: 최대 힙
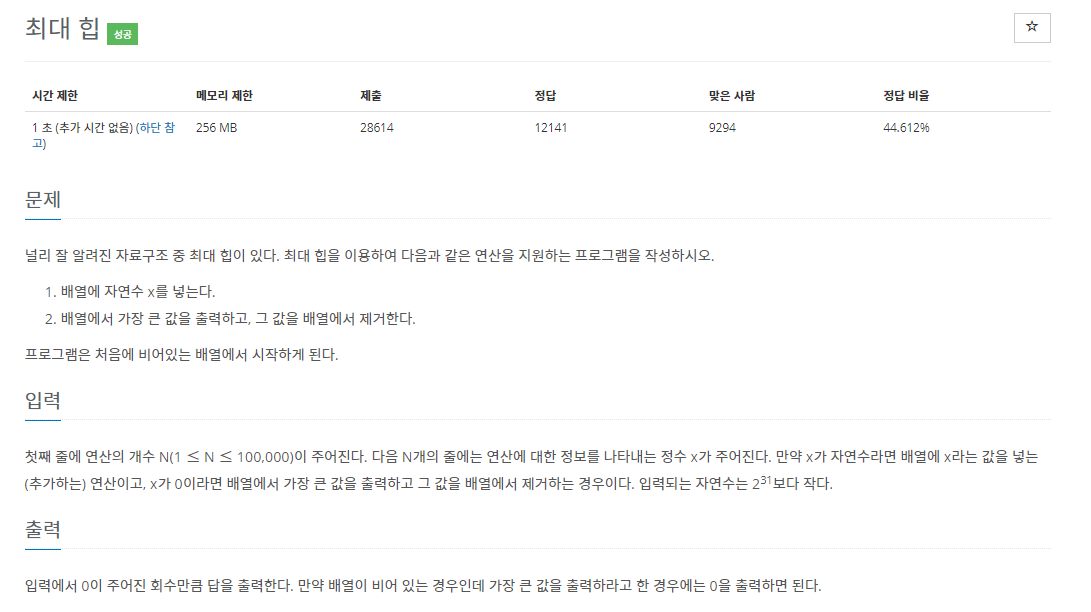
✔ 풀이를 위한 아이디어우선순위 큐 (Priority Queue)와 힙 (Heap)✔ 수정 전 코드 시간 초과약 1년도 더 전에 (벌써 1년이나 됐어?!) 자료구조 수업 시간에 배웠던 힙 (Heap). 까먹어서 다시 공부하였다. https://chanhuise
21.백준 7662번: 이중 우선순위 큐
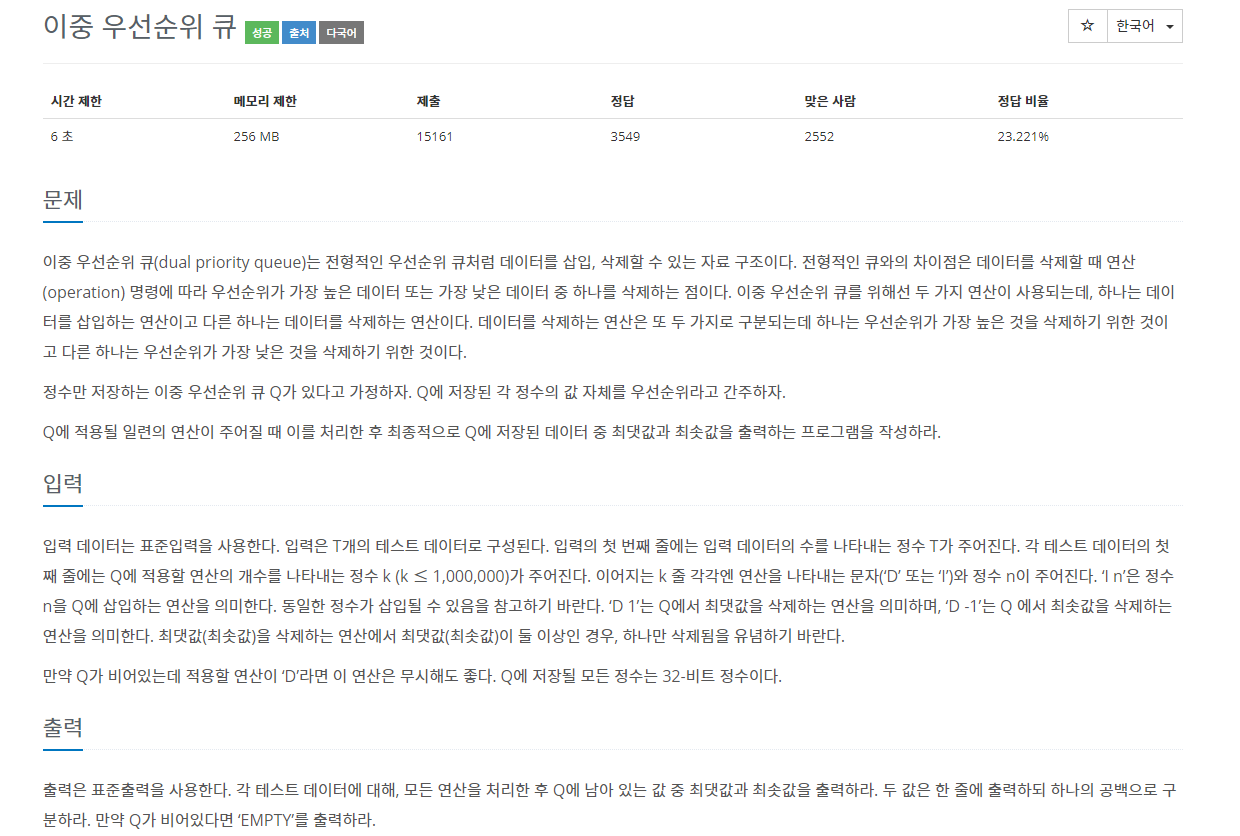
✔ 풀이를 위한 아이디어우선순위 큐 (Priority Queue)와 힙 (Heap)의 응용✔ 수정 전 코드처음 내 아이디어는 어설프지만 위의 그림과 같았다. Max Heap과 Min Heap에서 핵심적인 요소는 결국 index 0에 있는 최댓값과 최솟값이다. 따라서 두
22.백준 1931번: 회의실 배정
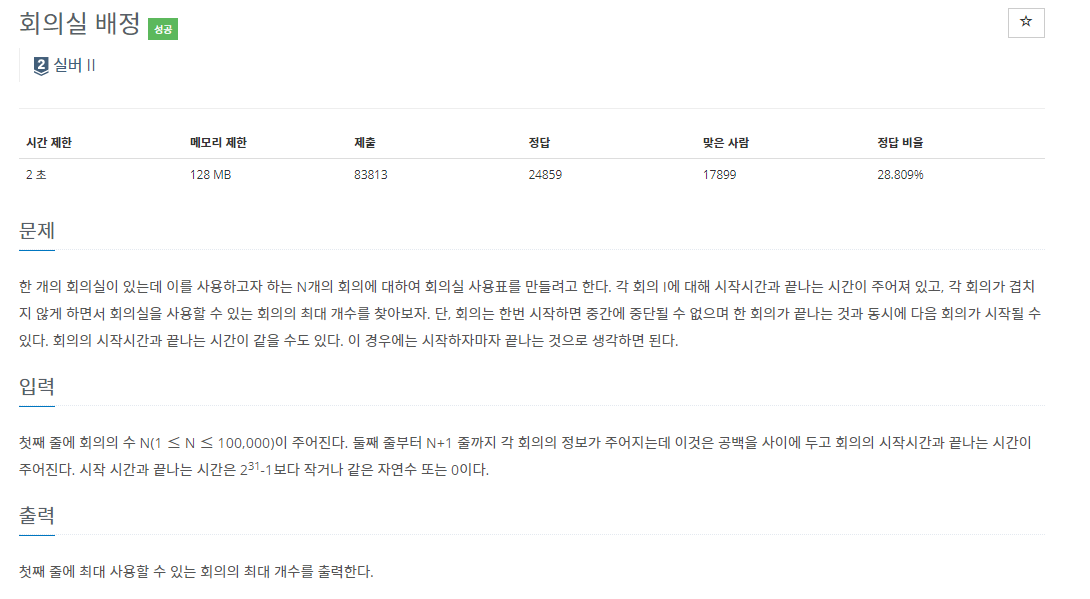
✔ 풀이를 위한 아이디어정렬 (Sorting) 과 그리디 알고리즘 (Greedy Algorithm)무엇을 기준으로 정렬해야 할지에 대한 고민✔ 수정 전 코드 시간 초과 + 틀렸습니다처음에 나는, 시작 시간을 기준으로 정렬한 뒤 그 안에서 종료 시간을 기준으로 정렬하는
23.백준 15664번: N과 M (1~12)
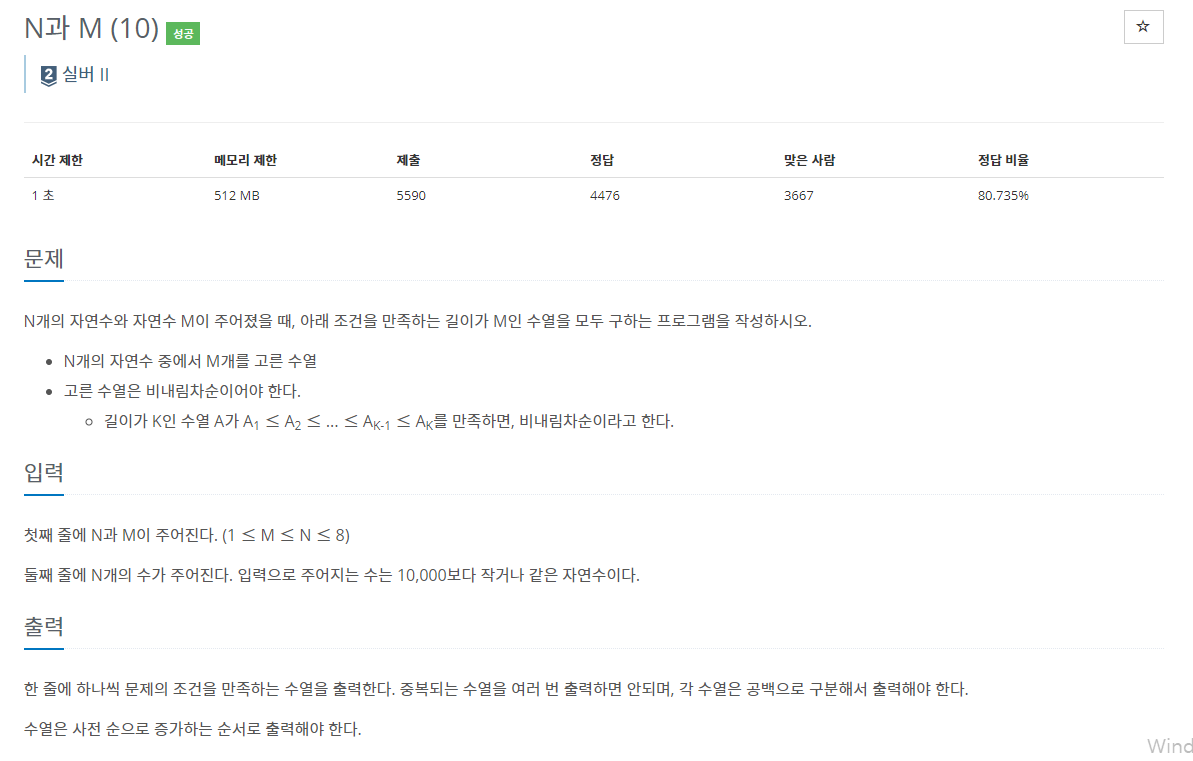
✔ 풀이를 위한 아이디어백 트래킹 (Back Tracking)✔ 핵심 코드위의 코드를 이해하는 것이 12개의 N과 M 문제를 푸는 열쇠라고 할 수 있다. 기존에 실제 스택 (Stack)을 활용하여 DFS를 구현했던 것과 달리, 백 트래킹은 재귀 함수의 호출이 스택 구조
24.백준 2630번: 색종이 만들기

✔ 풀이를 위한 아이디어분할 정복 (Divide and Conquer)재귀 (Recursion)✔ 코드어려워 보였지만, 생각보다 손쉽게 풀린 문제이다.check라는 함수는 탐색하고자 하는 영역 안에 있는 수들이 모두 같은 색인지 아닌지를 판단한다. 만일 모두 같은 색이
25.백준 1074번: Z

✔ 풀이를 위한 아이디어분할 정복 (Divide and Conquer)재귀 (Recursion)✔ 수정 전 코드 시간 초과사실 색종이 만들기 문제를 풀고 나면 쉽게 아이디어를 떠올릴 수 있다. 그래서 기분좋게 코드를 짜서 제출했더니 시간 초과가 나버렸다.Z 순서대로 순
26.백준 1149번: RGB거리
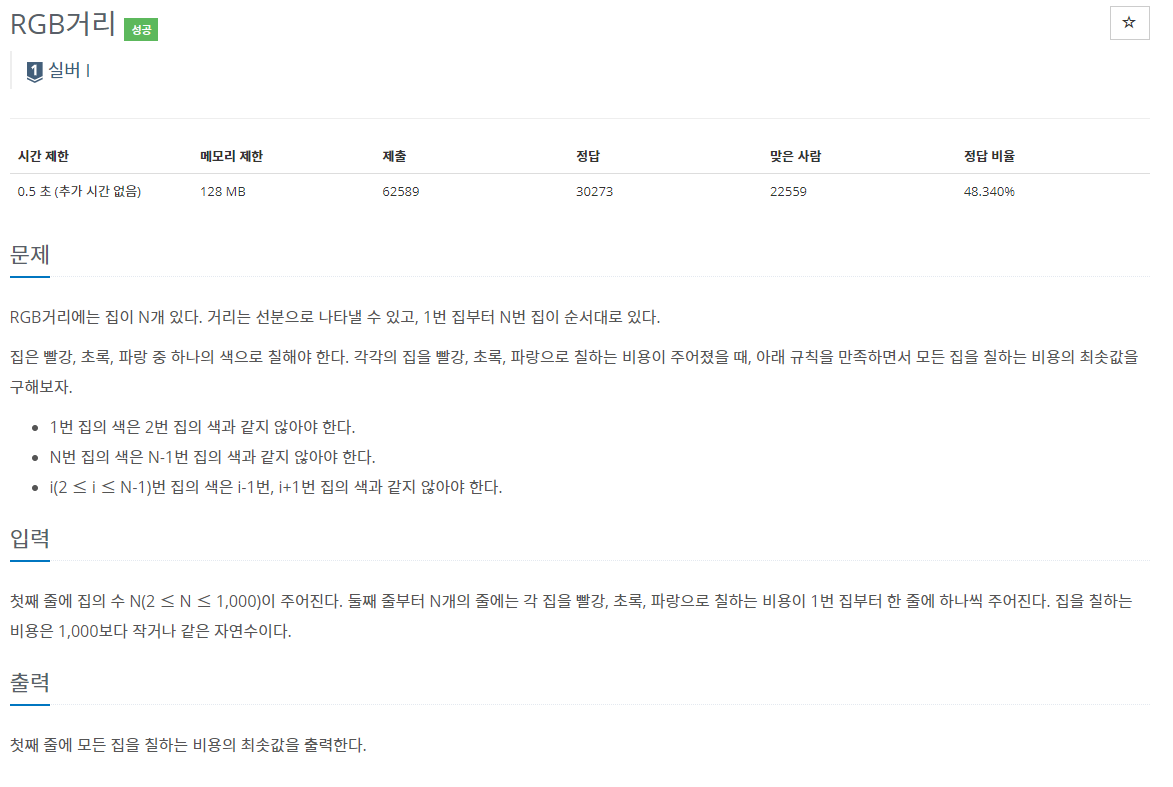
✔ 풀이를 위한 아이디어다이나믹 프로그래밍 (Dynamic Programming)✔ 수정 전 코드 틀렸습니다문제의 핵심은 잘 파악했다고 생각한다. 매 케이스마다 (N이 1씩 커질 때마다) 총 6가지 경우의 수가 생기는데, 이는 빨강으로 끝나는 경우, 초록으로 끝나는 경
27.백준 1016번: 제곱 ㄴㄴ 수
✔ 풀이를 위한 아이디어에라토스테네스의 체 (Eratosthenes Sieve)✔ 수정 전 코드 메모리 초과이전에 풀었던 백준 1978번 문제 (소수 찾기) 를 조금만 바꿔서 제출하였다. 에라토스테네스의 체는 큰 범위에 있는 소수들을 효율적으로 찾아낼 때 매우 효율적인
28.백준 11054번: 가장 긴 바이토닉 부분 수열
✔ 풀이를 위한 아이디어다이나믹 프로그래밍 (Dynamic Programming)✔ 백준 11053번: 가장 긴 증가하는 부분 수열 (수정 전 코드) 메모리 초과'가장 긴 바이토닉 부분 수열' 문제를 풀기 전에, 그 전 단계 문제라고 할 수 있는 '가장 긴 즈가하는 부
29.백준 12015번: 가장 긴 증가하는 부분 수열 2
✔ 풀이를 위한 아이디어Dynamic Programming 중 특별케이스인 LIS (Longest increasing Subsequence)bisect 표준 라이브러리를 활용한 이분 탐색 (Binary Search)✔ 코드이전에 풀었던 '가장 긴 증가하는 부분 수열'
30.백준 11725번: 트리의 부모 찾기
✔ 풀이를 위한 아이디어그래프 (Graph) 탐색 (DFS, BFS)트리 (Tree) 개념 이해✔ 수정 전 코드 시간 초과문제에 대한 설명이 부족해서, 문제 이해에 시간이 조금 걸리긴 했지만 해결은 간단하다.그래프 탐색 문제라고 봐도 무방할 정도이다. 다만 그래프를 트
31.백준 12865번: 평범한 배낭
✔ 풀이를 위한 아이디어다이나믹 프로그래밍 (Dynamic Programming)분할 가능하지 않은 배낭 문제 (knapsack 문제)✔ 알고리즘 설명야간 근무를 뛰며 고민해봐도 도저히 아이디어가 떠오르지 않아, 알고리즘 자체를 공부하기로 결심하였다. 밑의 그림은 직접
32.백준 9663번: N-Queen
✔ 풀이를 위한 아이디어브루트포스 알고리즘백 트래킹 (Back Tracking)✔ 정답 코드 (개선 전)문제의 조건을 만족 시키기 위해서는 같은 행, 같은 열, 그리고 두 갈래의 대각선 상에 다른 퀸이 없도록 해야한다. 한 행에 하나의 퀸만 들어갈 수 있기 때문에 각
33.백준 1991번: 트리 순회
✔ 풀이를 위한 아이디어트리 (Tree) 와 재귀 (Recursion)✔ 정답 코드자료구조 수업 과제로 BST ADT를 구현했던 때와는 다르게, 딕셔너리를 활용하여 비교적 심플하게 구현해보았다. 이전에 짰던 코드는 아래의 주소에서 볼 수 있다. (사실 정확히 말자하면,
34.백준 9251번: LCS
✔ 풀이를 위한 아이디어다이나믹 프로그래밍 (Dynamic Programming)LCS (Longest Common Subsequence, 최장 공통 부분 수열) 문제✔ 알고리즘 설명이 문제는 배낭 문제와 마찬가지로, 2차원 배열로 푸는 DP 문제이다. 복습하도록 하자
35.백준 1753번: 최단경로
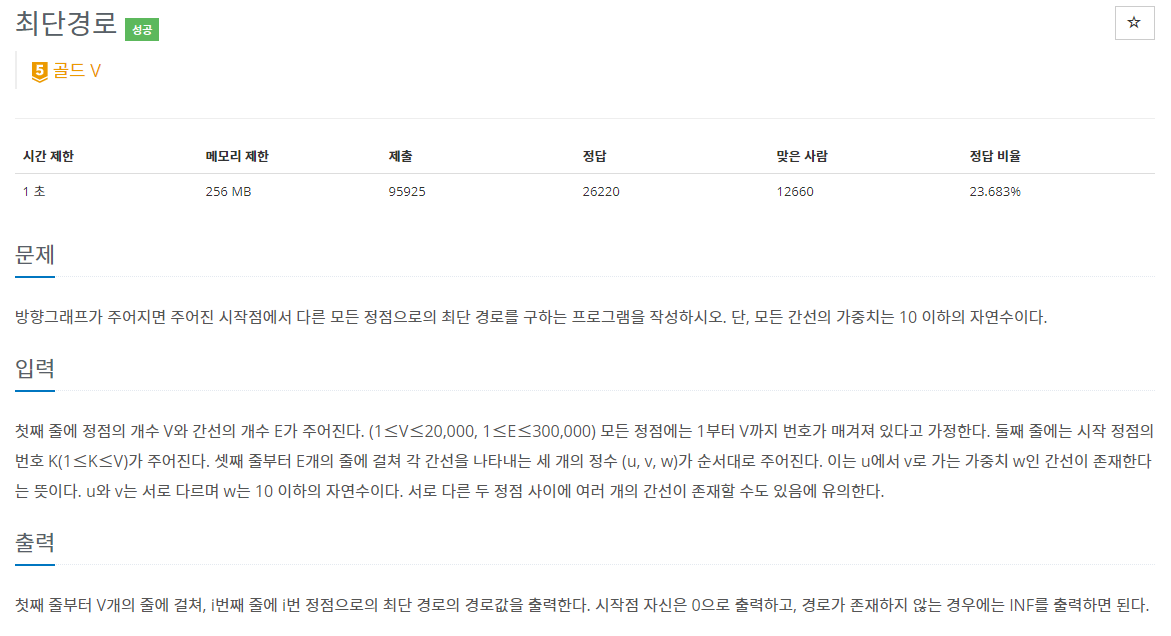
✔ 풀이를 위한 아이디어그래프 (Graph) 이론다익스트라 (Dijkstra) 알고리즘 (한 지점에서 다른 모든 지점까지의 최단 경로)✔ 알고리즘 설명다익스트라 알고리즘을 공부한 뒤에 코드를 짜보았다. https://www.youtube.com/watch?v=
36.백준 1629번: 곱셈
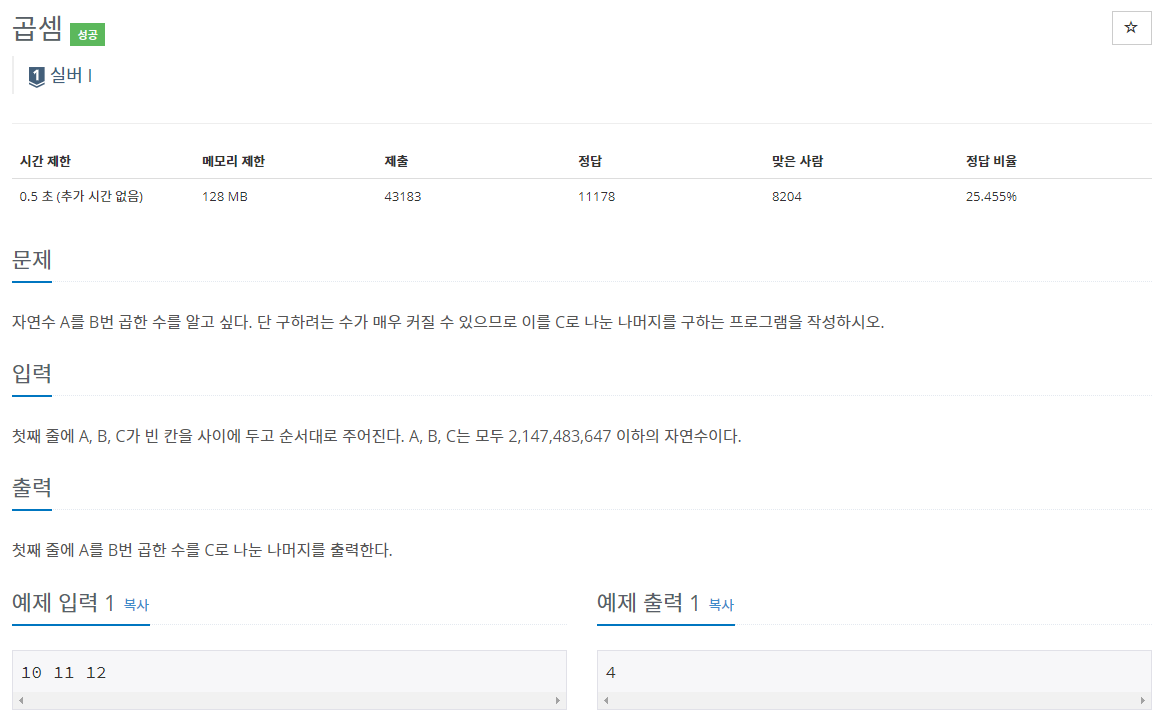
✔ 풀이를 위한 아이디어분할 정복 (Divide-and-conquer) 을 이용한 거듭제곱나머지 (Modulo) 연산 분배법칙✔ 수정 전 코드 시간 초과어떤 수를 N번 거듭제곱 한다고 했을 때, 일반적으로 그 알고리즘은 O(N)의 시간복잡도를 갖는다.위의 점화식과 같은
37.2206번: 벽 부수고 이동하기
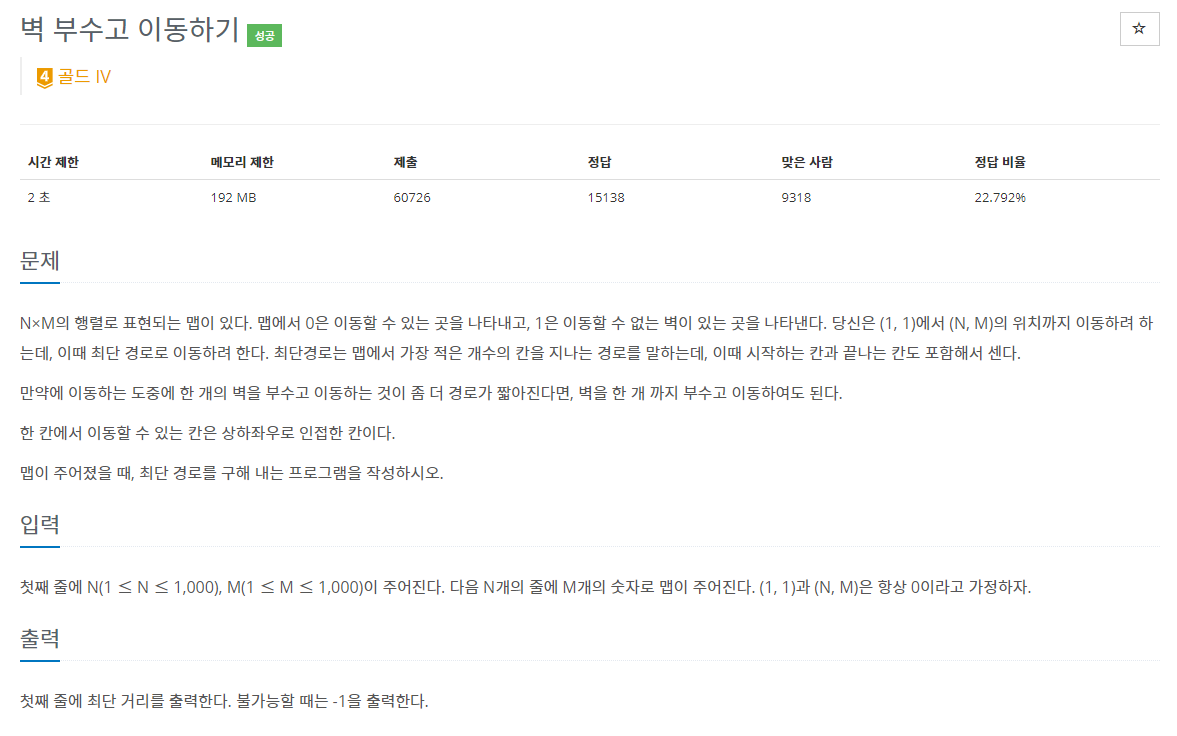
✔ 풀이를 위한 아이디어그래프 이론 + 너비 우선 탐색예외 케이스를 통한 오류 해결 + 논리적 사고력으로 케이스 분류✔ 오답 코드 1 틀렸습니다문제를 어떻게 풀어야할지 감이 아예 오지 않는 문제는 아니었다. 하지만 벽을 부술 수 있다는 조건 하나가 문제 풀이를 굉장히
38.백준 11404번: 플로이드
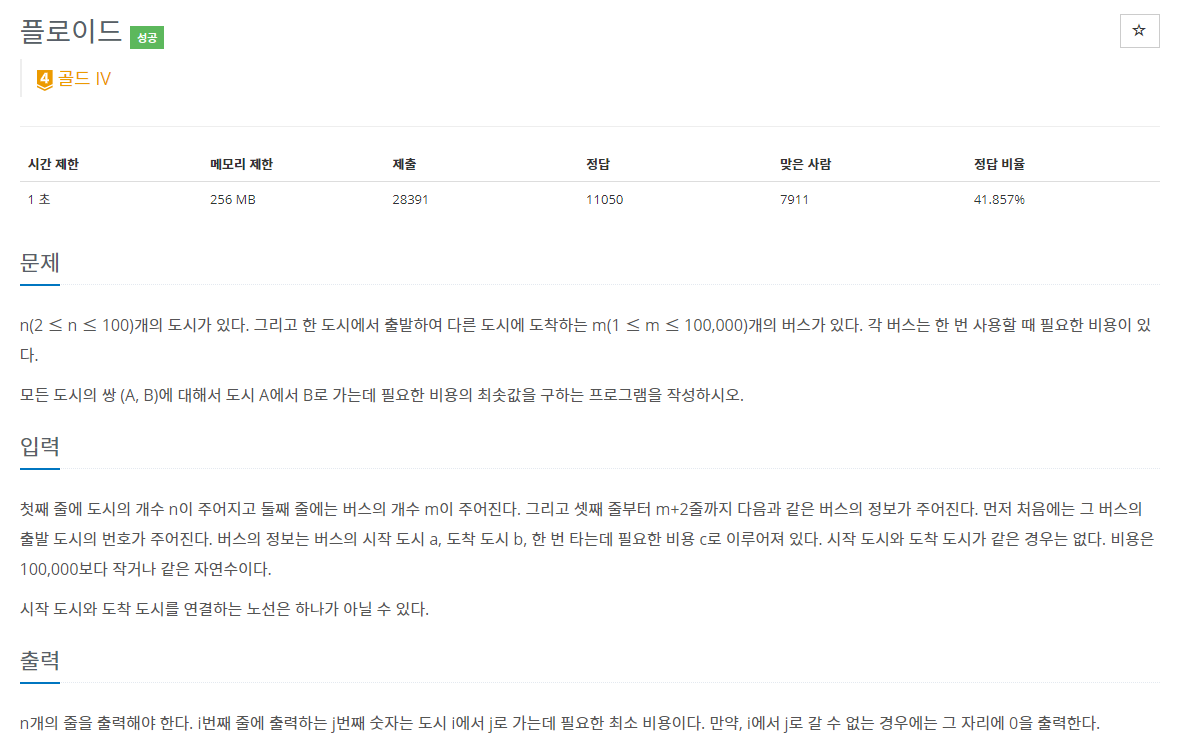
✔ 풀이를 위한 아이디어그래프 (Graph) 이론플로이드-와샬 (Floyd–Warshall) 알고리즘 (모든 지점에서 다른 모든 지점까지의 최단 경로)✔ 알고리즘 설명플로이드-와샬 알고리즘을 공부한 뒤에 코드를 짜보았다.https://www.youtube.co
39.백준 1967번: 트리의 지름
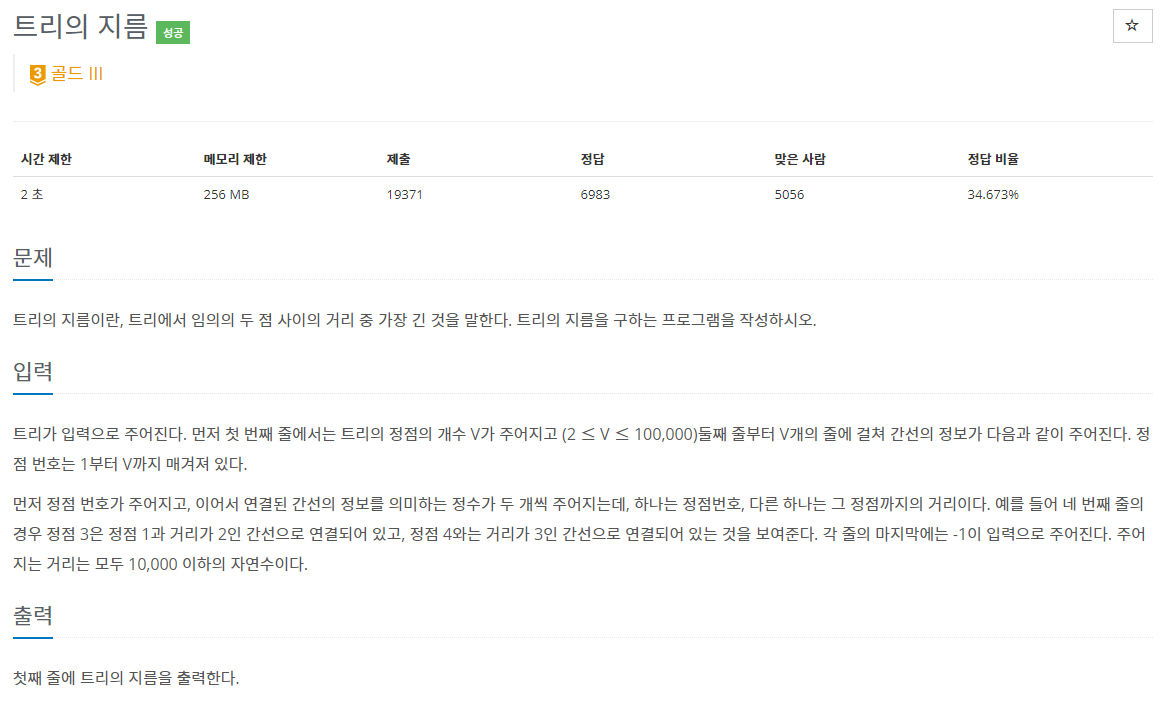
✔ 풀이를 위한 아이디어그래프 이론 + 그래프 탐색 (DFS or BFS)그래프로 표현되는 트리 (Tree) 의 이해 ✔ 오답 코드 틀렸습니다접근 방식문제의 힌트에서는 DFS를 활용해 풀으라고 말하고 있었다. 하지만, 나는 DFS 보다 후위 순회를 하는 것이 문제에서
40.백준 13549번: 숨바꼭질 3
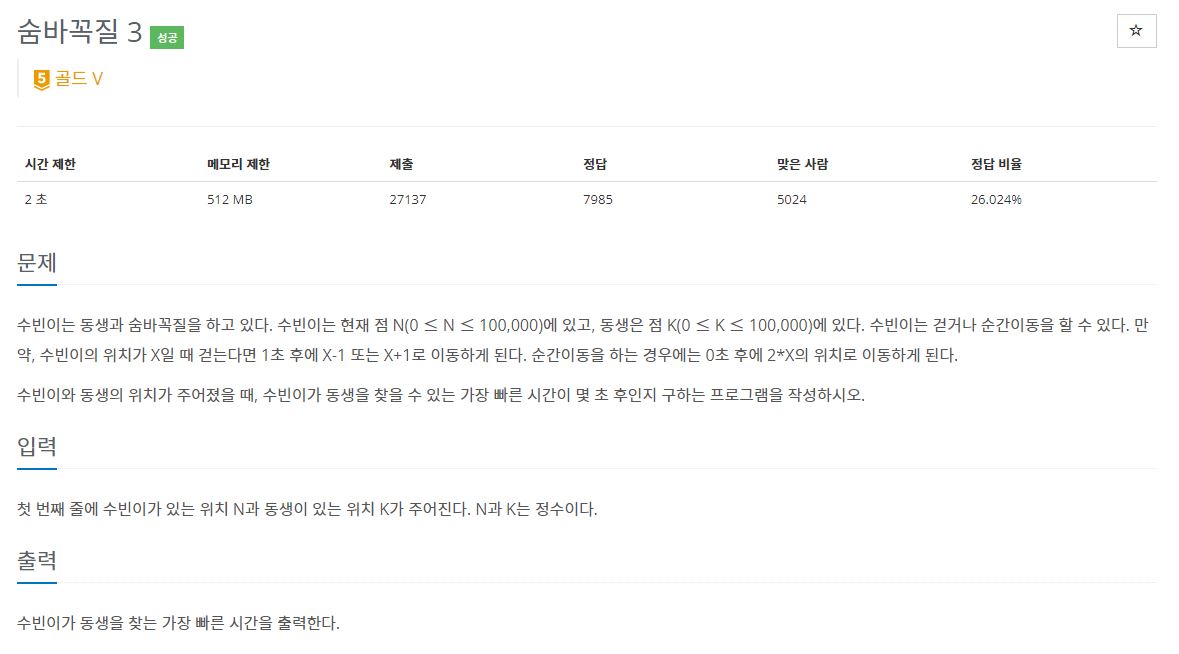
✔ 풀이를 위한 아이디어0-1 너비 우선 탐색 (BFS + 다익스트라)✔ 오답 코드 틀렸습니다접근 방식0-1 너비 우선 탐색 이라는 알고리즘이 따로 존재하는 줄 알고 구현에 앞서 알고리즘을 공부하려 했으나, BFS와 다익스트라 알고리즘을 합쳐놓은 것이라는 것을 깨닫고
41.백준 2407번: 조합
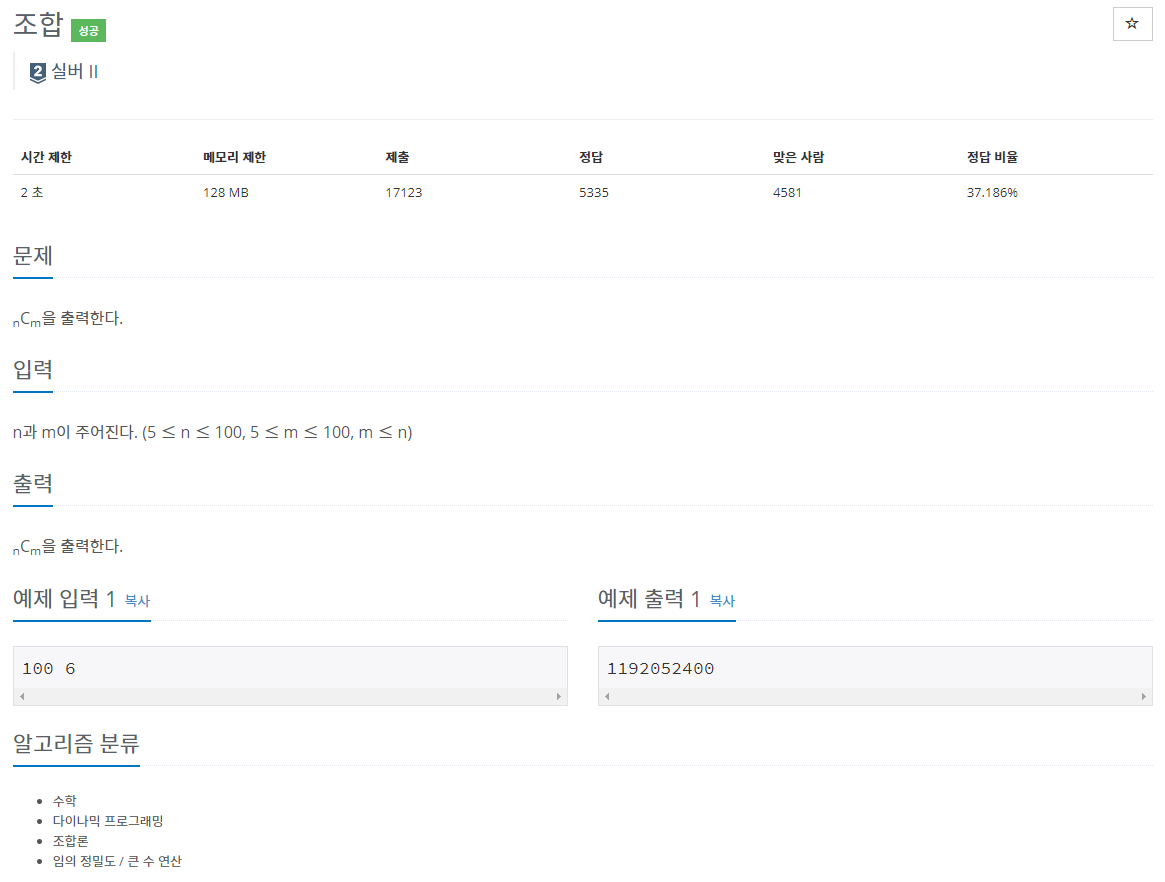
✔ 풀이를 위한 아이디어다이나믹 프로그래밍 (Dynamic Programming)조합론 n_C_r = n-1_C_r-1 + n-1_C_r 임의 정밀도 / 큰 수 연산 => Python에서는 상관 X✔ 정답 코드우선, 조합을 DP로 풀어야한다는 점에서 n_C_r =
42.백준 1918번: 후위 표기식
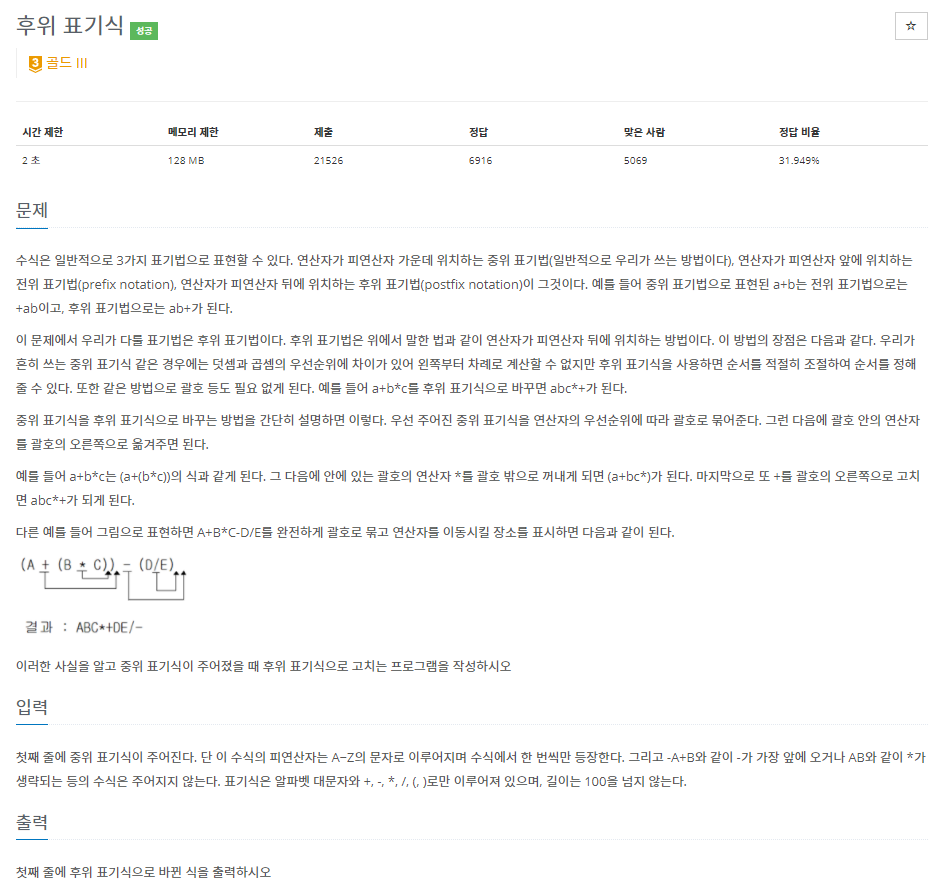
✔ 풀이를 위한 아이디어자료구조 중 스택 (Stack)후위 표기식의 개념적 이해✔ 후위 표기식이란?우리가 일반적으로 사용하는 중위 표기식 (infix) 과 다르게, 후위 표기식 (postfix) 은 연산자를 피연산자 뒤에 두는 방법왼쪽부터 순서대로 계산할 수 있기 때문
43.백준 2263번: 트리의 순회
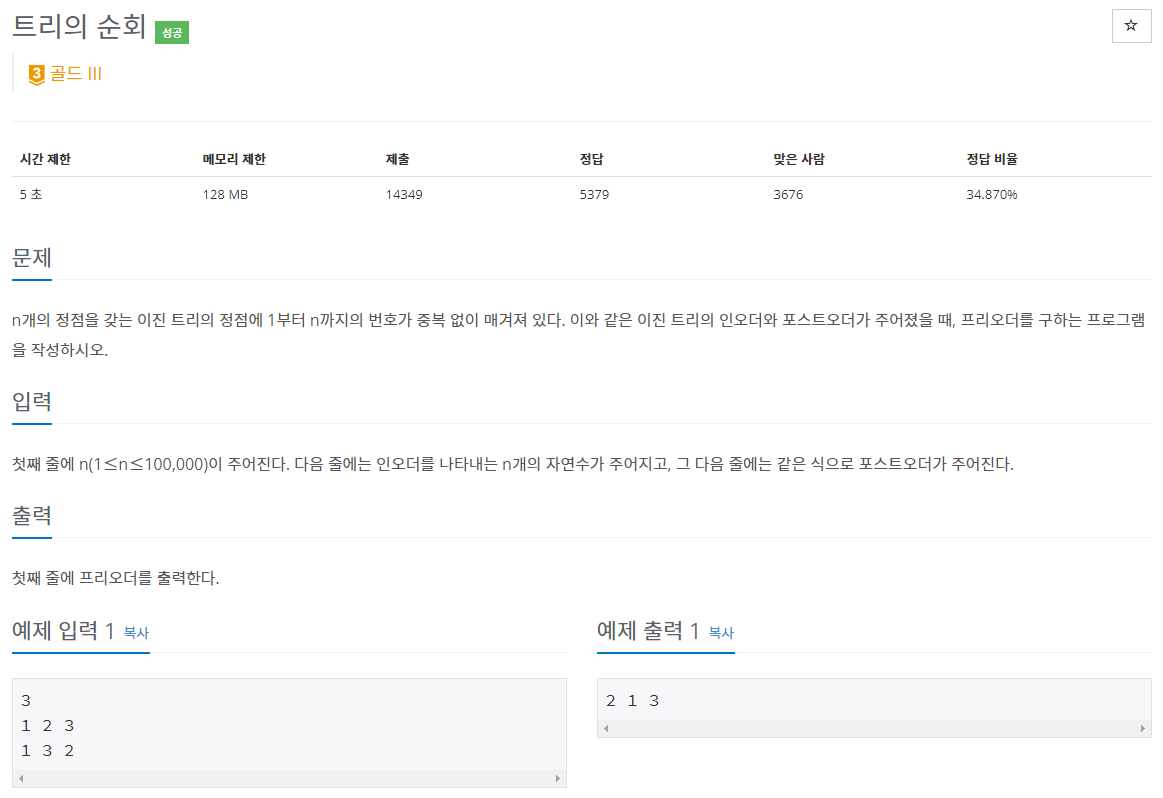
✔ 풀이를 위한 아이디어자료구조 중 트리 (Tree), 그리고 트리 순회의 응용분할 정복 (Divide-and-conquer algorithm)재귀 (Recursion)✔ 트리 순회 심화편일반적인 트리 순회에 대한 개념은 다음 게시물을 참조하자 - https:
44.백준 11657번: 타임머신
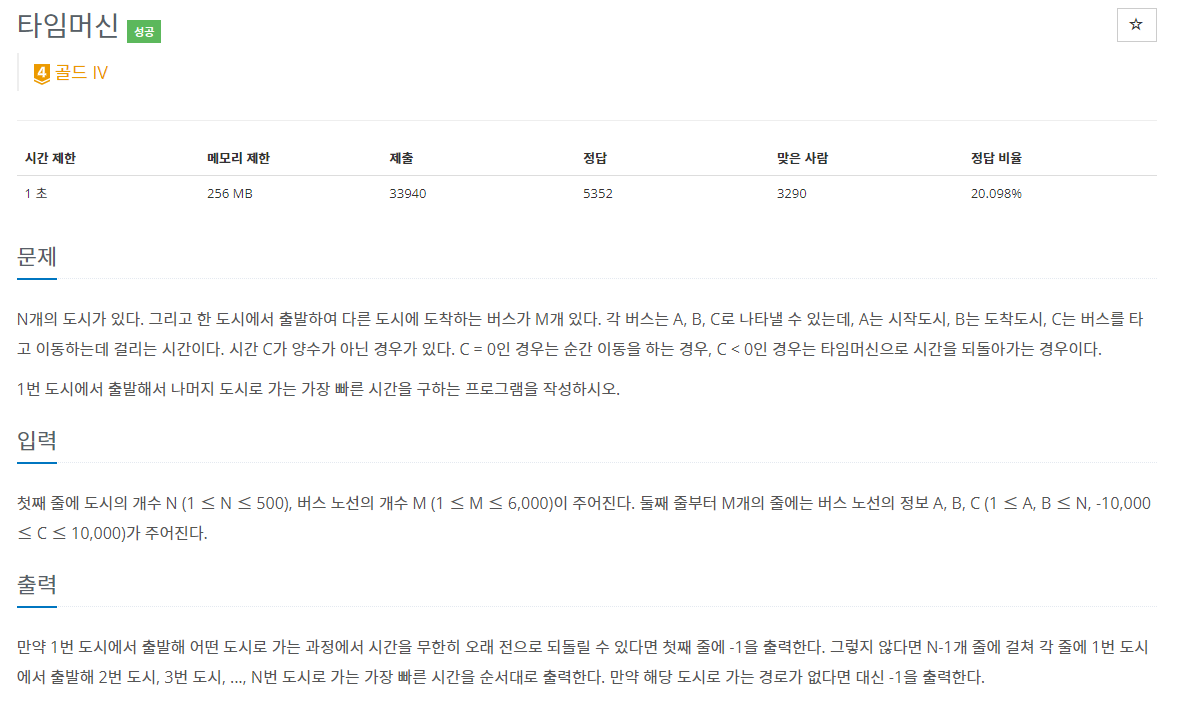
✔ 풀이를 위한 아이디어그래프 (Graph) 이론벨만-포드 알고리즘 (Bellman-Ford’s algorithm)✔ 알고리즘 설명벨만-포드 알고리즘을 공부한 뒤에 코드를 짜보았다. https://www.youtube.com/watch?v=Ppimbaxm8d8
45.백준 1865번: 웜홀
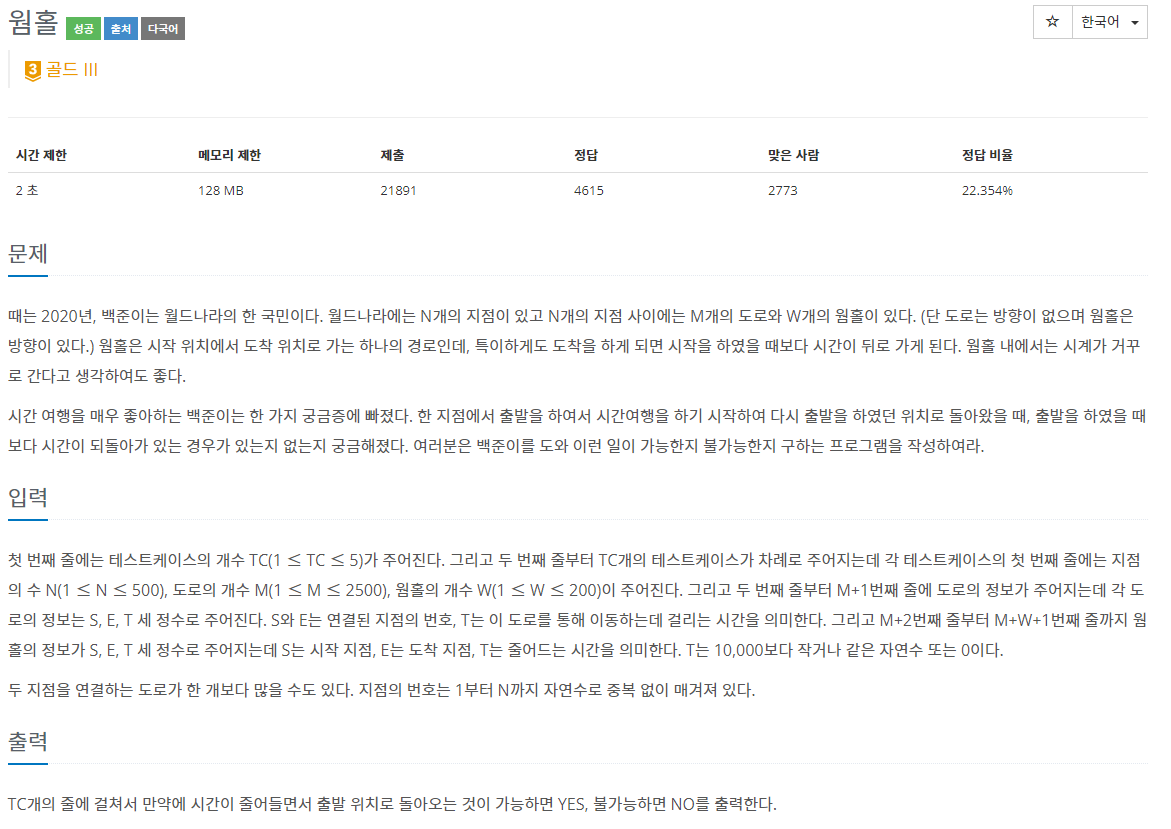
✔ 풀이를 위한 아이디어그래프 (Graph) 이론벨만-포드 알고리즘 (Bellman-Ford’s algorithm)✔ 개요이 문제의 핵심은 '음수 사이클의 존재 여부'를 판단하는 것인데, 이전에 풀었던 '타임머신' 문제의 코드를 조금 변형해줘야 맞출 수 있었다.http
46.백준 11444번: 피보나치 수 6
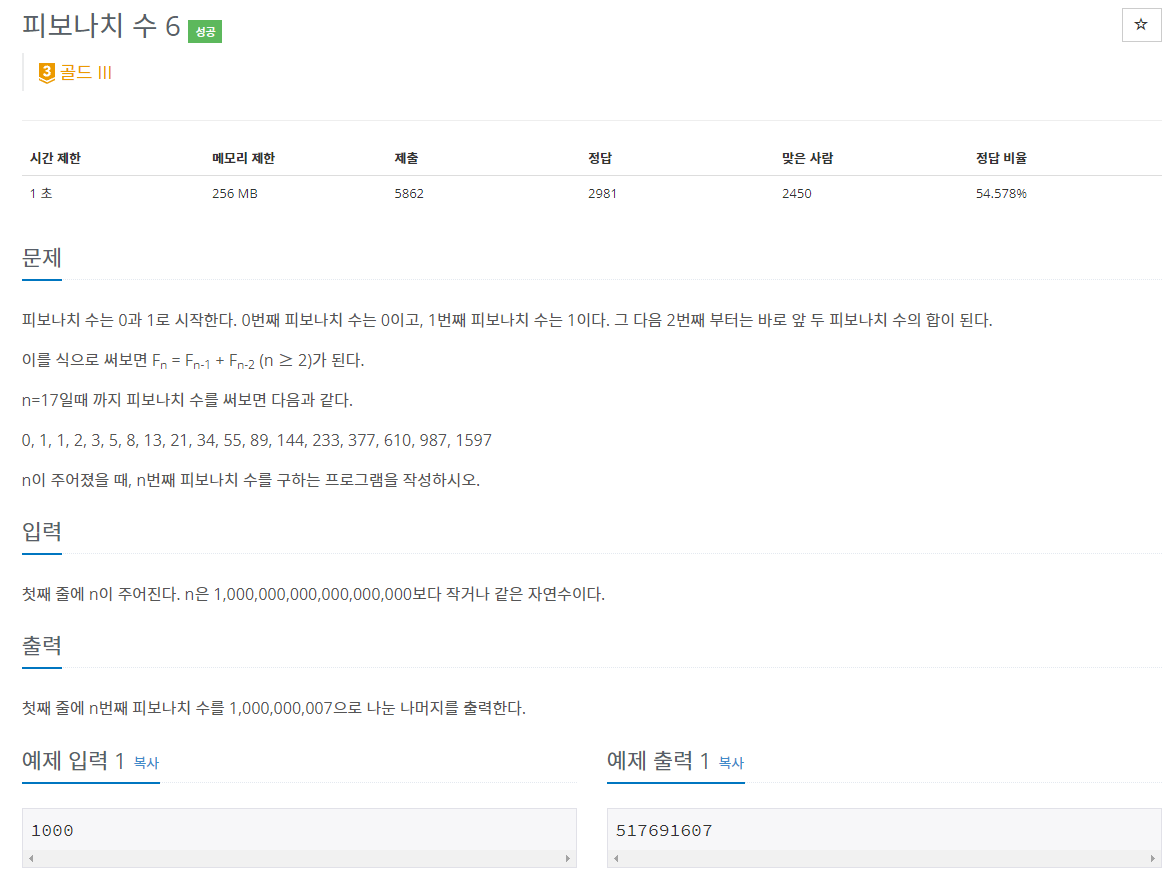
✔ 풀이를 위한 아이디어행렬의 곱셈을 활용해 피보나치 수 구하기분할 정복을 이용한 거듭제곱✔ 개요이 문제를 풀기 위해서는, 행렬의 곱셈을 활용해 피보나치 수를 구하는 방법을 알아야 한다.대각화로 피보나치 수열의 일반항 구하기: https://www.youtub
47.백준 12851번: 숨바꼭질 2 + 13913번: 숨바꼭질 4
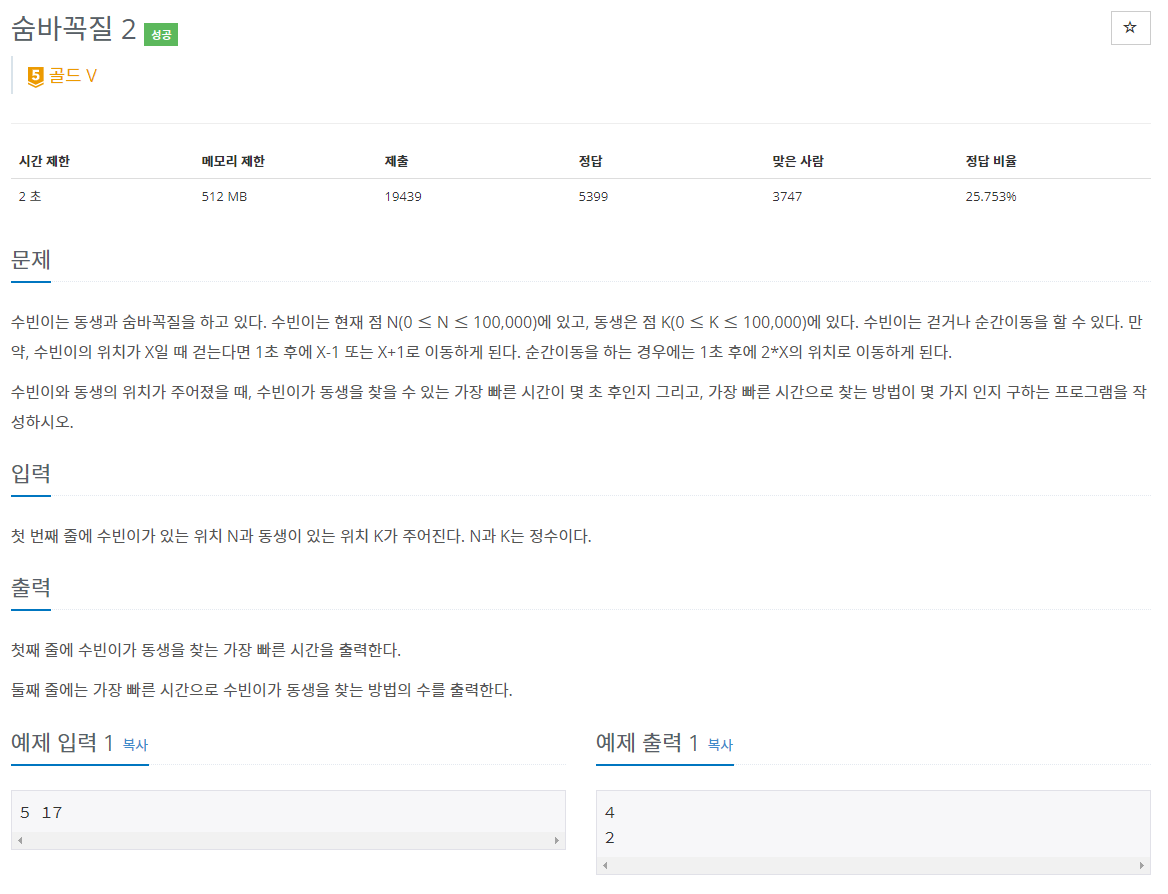
✔ 풀이를 위한 아이디어행렬의 곱셈을 활용해 피보나치 수 구하기분할 정복을 이용한 거듭제곱✔ 개요이 문제를 풀기 위해서는, 행렬의 곱셈을 활용해 피보나치 수를 구하는 방법을 알아야 한다.대각화로 피보나치 수열의 일반항 구하기: https://www.youtub
48.백준 14502번: 연구소
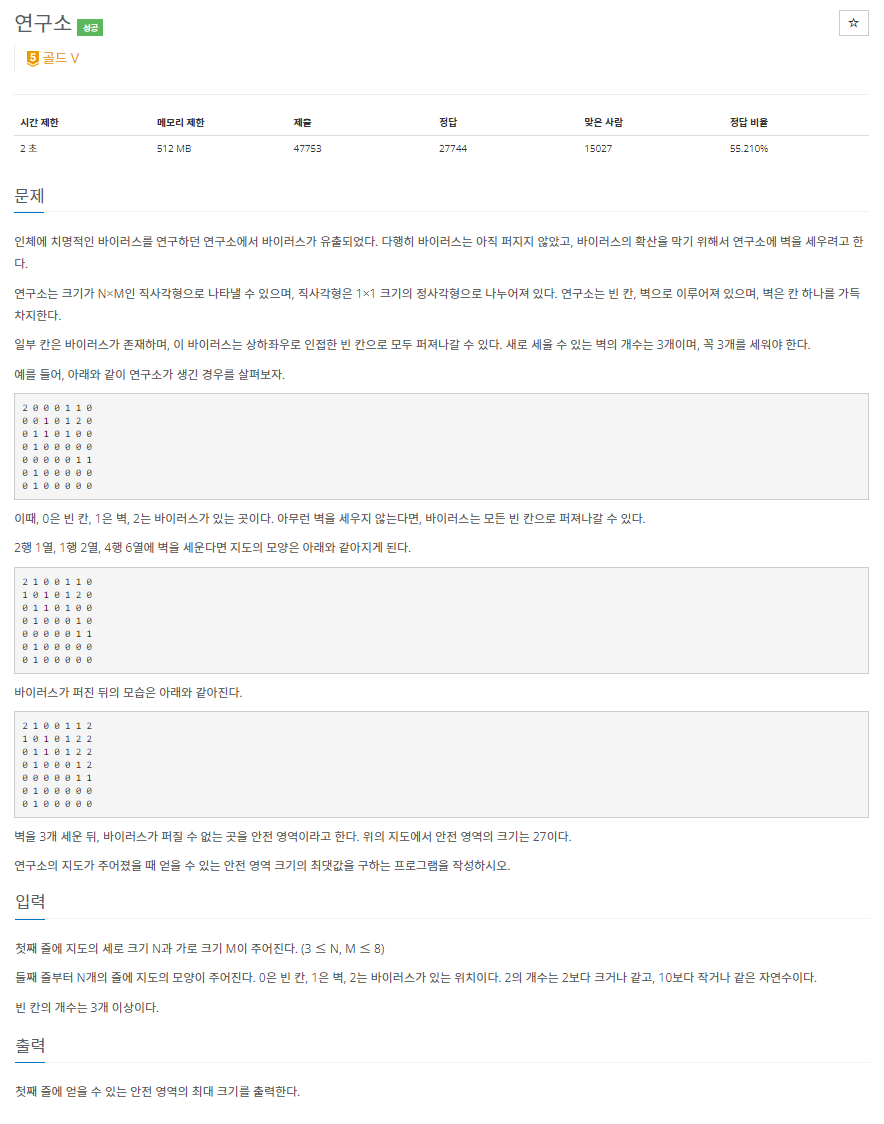
✔ 풀이를 위한 아이디어그래프 (Graph) 탐색 중 너비 우선 탐색 (BFS)브루트포스 알고리즘 (Brute-force search)✔ 정답 코드코드의 길이가 길기는 하지만, 브루트포스 알고리즘이다보니 아이디어 자체는 크게 어렵지 않았다. 다만 사용한 모듈이 조금 새
49.setrecursionlimit() 함수에 관한 오해와 진실

Python으로 PS를 할 때 최대 재귀 한도 깊이의 제한으로 인해 Recursion Error가 발생하는 것을 막기 위해 setrecursionlimit() 함수를 사용하곤 한다.BOJ 11437번 LCA 문제 (https://www.acmicpc.net/p