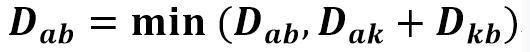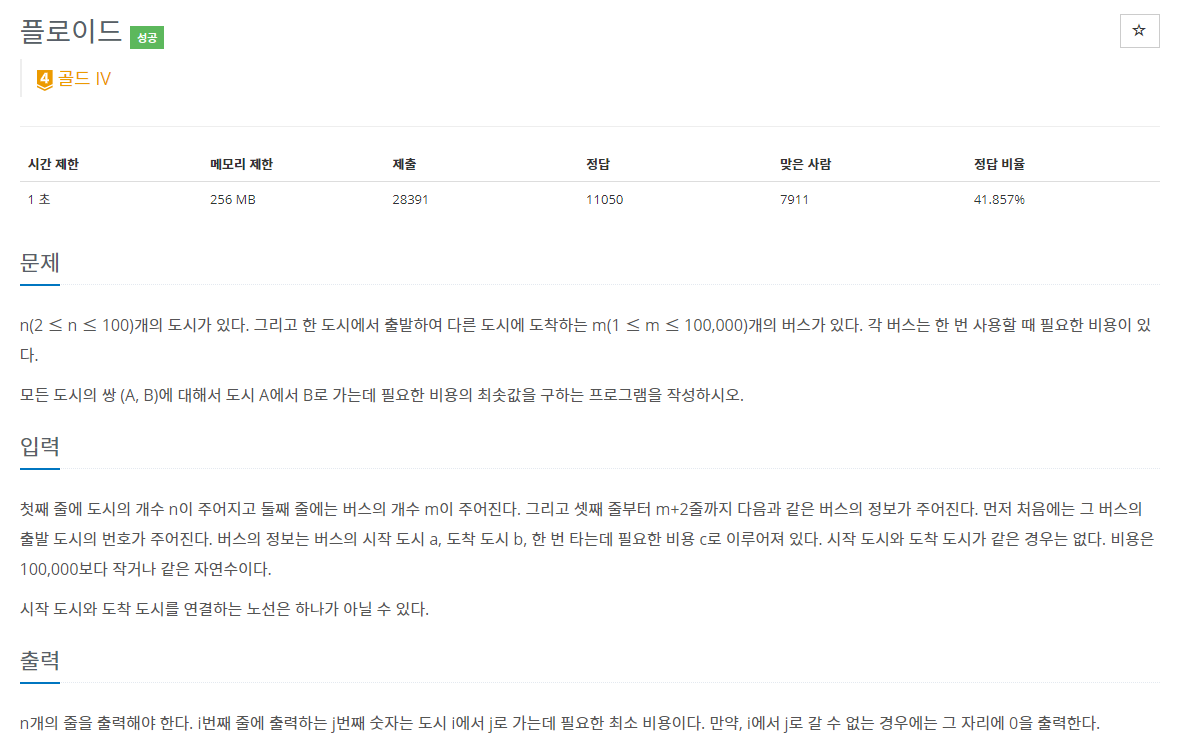
✔ 풀이를 위한 아이디어
-
그래프 (Graph) 이론
-
플로이드-와샬 (Floyd–Warshall) 알고리즘 (모든 지점에서 다른 모든 지점까지의 최단 경로)
✔ 알고리즘 설명
-
플로이드-와샬 알고리즘을 공부한 뒤에 코드를 짜보았다.
-
https://www.youtube.com/watch?v=hw-SvAR3Zqg 의 알고리즘 설명부분만 참고하였다.
플로이드-와샬 알고리즘 개요
-
모든 노드에서 다른 모든 노드까지의 최단 경로를 모두 계산하는 알고리즘이다.
-
다익스트라 알고리즘과 다르게 최단거리를 갖는 노드를 찾는 과정이 필요 없다. (다익스트라 알고리즘에서는 이를 구현하기 위해서 최소 힙을 사용하였다.)
-
3중 for문을 돌며 2차원 테이블에 최단거리 정보를 저장하는 방식으로 구현한다. (다익스트라 알고리즘은 한 지점에서 다른 모든 지점만 구하면 됐으므로 1차원 배열을 사용했다.)
-
이는 다이나믹 프로그래밍 유형에 속한다. 왜냐하면 노드의 개수 N번 만큼 반복하며 '점화식에 맞게' 2차원 배열을 갱신하기 때문이다. (다익스트라 알고리즘은 그리디 알고리즘에 속한다.)
-
다익스트라 알고리즘보다 구현 난이도는 낮은 편에 속하며, 시간복잡도가 O(N^3)이므로 노드 및 간선의 개수가 적을 때 사용한다.
알고리즘 동작 과정
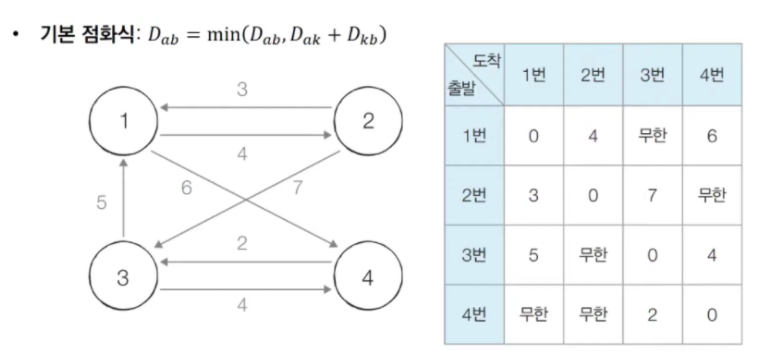
- 2차원 테이블을 초기화 한다. (갈 수 없는 경우는 거리를 INF로 설정하고, 자신으로부터 자신으로까지의 거리는 0으로 설정한다.)
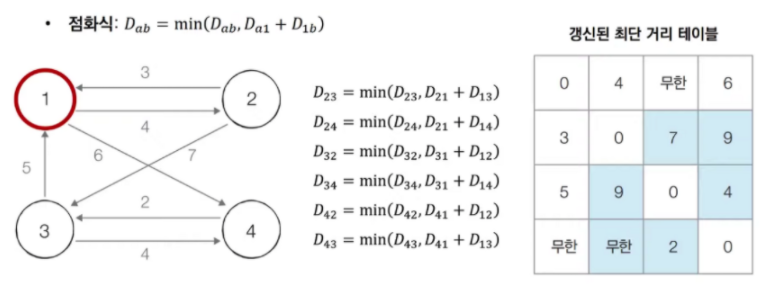
-
노드가 4개라면, 자신을 제외한 나머지 3개 중에서 2개를 고르는 경우의 수만큼 갱신한다. 이때, 자신이 시작점이나 끝점에 있는 경우를 제외하며, 대각선 상에 있는 거리가 0인 경우도 제외한다.
-
갱신을 할 때에는 기본 점화식에 의해서, 기존에 테이블에 있던 값과 현재 검토 중인 노드를 거쳐갈 때의 값을 비교한다.
플로이드-와샬 알고리즘의 기본 점화식
- 위의 과정을 노드의 개수만큼 반복한다.
✔ 전체 코드
import sys
n = int(sys.stdin.readline())
m = int(sys.stdin.readline())
INF = float('inf')
table = [[INF]*n for _ in range(n)] # 무한대로 초기화
for _ in range(m):
a, b, c = map(int, sys.stdin.readline().split())
if table[a-1][b-1] == INF:
table[a-1][b-1] = c
else: # 기존에 값이 있다면 최솟값만 남기기
table[a-1][b-1] = min(table[a-1][b-1], c)
for i in range(n):
table[i][i] = 0 # 자신에서 자신으로 가는 경우는 0으로 초기화
for current in range(n):
for start in range(n):
for end in range(n):
if start == current or end == current or start == end: # 갱신할 필요 없는 경우
continue
table[start][end] = min(table[start][end], table[start][current] + table[current][end])
# 기본 점화식에 따른 갱신, y축 방향으로 시작 지점들이 있고 x축 방향으로 도착 지점들이 있다.
for start in range(n):
for end in range(n):
if table[start][end] == INF: # 갈 수 없는 경우 0을 출력
print("0 ", end="")
else:
print("{} ".format(table[start][end]), end="")
print()

- 마지막 부분에 INF 값의 출력을 0으로 처리해주지 않아서 한 차례 '틀렸습니다' 를 받았다.
이 알고리즘 역시 오랫동안 쓰지 않으면 까먹을 수 있으므로, 반드시 복습하도록 하자!