백준 11444번: 피보나치 수 6

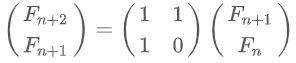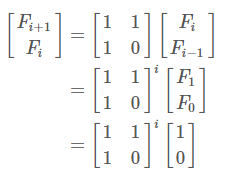
✔ 풀이를 위한 아이디어

• 행렬의 곱셈을 활용해 피보나치 수 구하기
• 분할 정복을 이용한 거듭제곱
  
  

✔ 개요

• 이 문제를 풀기 위해서는, 행렬의 곱셈을 활용해 피보나치 수를 구하는 방법을 알아야 한다.
  대각화로 피보나치 수열의 일반항 구하기: https://www.youtube.com/watch?v=uX2IsIykLJc
  위의 영상을 공부했는데, 실제 문제풀이에서는 대각화의 개념까지는 활용할 필요가 없었고, 아래의 공식만을 활용하여 구해냈다.
  

이 방법은 n번째 피보나치 수를 구하는 문제에서 n이 매우 클 경우에 활용하기 적절하다.

• 또한, 분할 정복을 활용하여 거듭제곱을 해야하는데, 방식은 이전에 풀었던 문제와 동일하다. https://velog.io/@dlehdtjq00/백준-1629번-곱셈

✔ 전체 코드

def matrixMultipli(row1, col1row2, col2, matrix1, matrix2):
    result = [[0 for _ in range(col2)] for _ in range(row1)]
    for i in range(row1):
        for j in range(col2):
            for k in range(col1row2):
                result[i][j] += matrix1[i][k] * matrix2[k][j]
            result[i][j] %= 1000000007

    return result


def devideConquer(n, matrix):
    if n == 1:
        return matrix
    tmp = devideConquer(n//2, matrix)
    if n % 2 == 0:
        return matrixMultipli(2, 2, 2, tmp, tmp)
    else:
        return matrixMultipli(2, 2, 2, matrixMultipli(2, 2, 2, tmp, tmp), matrix)


n = int(input())
A = [[1, 1], [1, 0]]

if n >= 3:
    result = matrixMultipli(2, 2, 1, devideConquer(n-1, A), [[1], [0]])
    print(result[0][0])  # 여기선 굳이 나머지 연산 필요 X (<-> 행렬제곱 문제)
else:
    print(1)

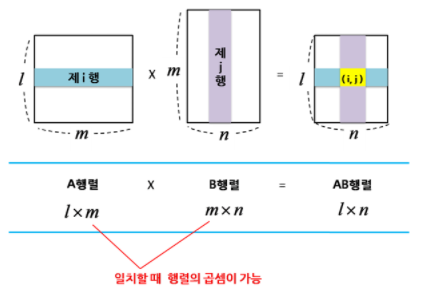
• 행렬의 곱셈 구현
  

def matrixMultipli(row1, col1row2, col2, matrix1, matrix2):
    result = [[0 for _ in range(col2)] for _ in range(row1)]
    for i in range(row1):
        for j in range(col2):
            for k in range(col1row2):
                result[i][j] += matrix1[i][k] * matrix2[k][j]
            result[i][j] %= 1000000007

    return result

두 행렬을 곱하기 위해서는 행렬 1의 column과 행렬 2의 row가 같아야한다. 또한, 곱셈의 결과에 해당하는 행렬은 행렬 1의 row와 행렬 2의 column을 가지고 있다.
행렬의 곱셈법에 따라서 위와 같이 삼중 for문을 활용해 구현해주면 된다. 1000000007로 나눈 나머지 값을 구하라고 했으므로, % 연산자를 활용하여 2차원 배열에 넣어준다.

• 행렬의 곱셈을 활용해 피보나치 수 구하기
  

n = int(input())
A = [[1, 1], [1, 0]]
result = matrixMultipli(2, 2, 1, devideConquer(n-1, A), [[1], [0]])

print(result[0][0])  # 여기선 굳이 나머지 연산 필요 X (<-> 행렬제곱 문제)

위의 식을 통해 n번째 피보나치 수, 즉 F_n을 구하기 위해서는 [[1, 1], [1, 0]] 이라는 행렬을 n-1번 거듭제곱 해야함을 알 수 있다. 또한, 그 결과값에 [[1], [0]]을 곱해주어야 한다.
따라서, 우선 devideConquer 함수를 활용해 A 행렬을 n-1번 거듭제곱 해주고 (분할 정복의 구현은 아래에서 다룰 것이다), 추가적으로 [[1], [0]] 행렬을 곱해준다.
연산의 결과인 행렬에서 F_n은 row 0, column 0에 위치하고 있으므로, result[0][0]을 출력해주면 된다. 전체 코드처럼, n < 3인 경우는 따로 처리해주는 것도 잊지 말자.

• 분할 정복 구현

def devideConquer(n, matrix):
    if n == 1:
        return matrix
    tmp = devideConquer(n//2, matrix)
    if n % 2 == 0:
        return matrixMultipli(2, 2, 2, tmp, tmp)
    else:
        return matrixMultipli(2, 2, 2, matrixMultipli(2, 2, 2, tmp, tmp), matrix)

자신을 재귀적으로 호출하며 n번 만큼 행렬을 곱해주는 (제곱을 수행하는) 함수이다. 직접 구현한 행렬의 곱셈 함수를 사용했을 뿐, 구조 자체는 이전에 풀었던 문제와 동일하기 때문에 설명은 생략하겠다.