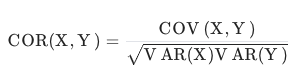9-1. 들어가며
학습 목표
- 시계열 데이터의 특성 + 안정적(Stationary) 시계열 이해하기
- ARIMA 모델: AR, MA, Diffencing 이해 및 적용하기
- 주식 데이터에 대한 ARIMA 적용하기
9-2. 시계열 예측이란(1) 미래를 예측한다는 것은 가능할까?
미래 예측은 불가능한 것
- 굳이 예측하려면, 2가지 전제가 있어야만 예측 가능
- 과거의 데이터에 일정한 패턴이 발견됨
- 과거의 패턴은 미래에도 동일하게 반복됨
즉, 안정적(Stationary) 데이터에 대해서만 미래 예측 가능
- 안정적?
- 시계열 데이터의 통계적 특성이 변하지 않는다는 의미
- 시간 변화와 무관하게 일정 프로세스가 있다는 것
- ex) 날씨는 불규칙 -> 연 단위 기후 변화 일정 패턴 유지 시 안정성에 의해 내일의 기온이 어느 정도 오차 범위 내에서 예측 될 것
Q. 유가 변화 예측 시, 위성 사진 등의 추가적 데이터를 활용한다면 -> 이것도 시계열 예측일까?
A. 시계열 예측이 맞다고 생각.
그 예로, 위성 사진의 경우에도 일정 주기로 촬영되는 특성이 있기 때문에 연속적 데이터셋이 만들어질 것이고 변화를 관찰하여 사용할 수 있기 때문에 시계열 예측이 맞음.
답변 : 과거 유가 변동 데이터만 이용할 경우 시계열 예측이 맞으나, 유가가 아닌 다른 성격의 데이터가 활용될경우 엄밀하게 봤을 때 시계열 예측이 아님
Q. 유가 변화 예측을 위해 이전 유가 변화 데이터만 활용하지 않고, 다른 데이터를 추가로 활용하는 이유는?
A. 유가의 변화에 영향이 미치게 되는 다른 밀접한 변화 요인들로 인해 발생된 결과 지표들도 있을 수 있기 때문이 아닐까.
답변
- 이전 유가만 활용
- 임의로 결정된 전제 -> "원유 시장이 외부 영향 없이 자체적으로 유가를 결정하는 안정적 프레세스가 있을 것"
- 국제 유가는 국가 간 분쟁, 경제 호황/불활 등 외부 요소가 많고 가격을 결정하는 수요-공급의 균형점이 끊임없이 변화함
- 즉, 외부 요인을 고려할 수 있는 보조 데이터 활용이 필요한 것
시계열 데이터 분석은 완벽한 미래 예측을 보장하지 않는다
- 미처 예측 못한 외부 변수로 인해 *전제가 훼손될 여지가 있음
- *전제 : 안정성(stationarity)
- 이러한 문제에도 불구하고, 시계열 데이터 분석 ➡️ 프로세스 내제적 시간 변화 묘사에 꽤 좋은 성능을 보임
9-3. 시계열 예측이란(2) Stationary한 시계열 데이터
👉 참고: 현재 노드에서의 Stationary Time-Series, Stationary, 안정적 시계열, 안정성 == 정상성과 같은 의미
시간이 흘러도 일정해야하는 통계적 특성
-
평균
- 모든 데이터의 합을 개수로 나눈 것
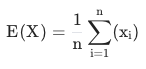
- 모든 데이터의 합을 개수로 나눈 것
-
분산
- Variance
- 평균에서 떨어져 있는 정도
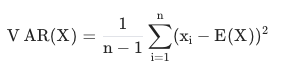
-
공분산
- Covariance
- 변수가 2개일 때의 분산
- 각 변수 분포의 관련성을 수치로 표현
- 각 변수 평균의 편차를 곱한 것을 -> 평균
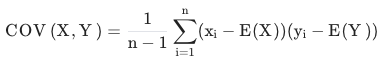
참고) 상관관계(Correlation)
- 공분산을 각 분산으로 다시 나눔 -> 공분산의 (-1, 1) 범위 스케일링
- 양의 상관관계 : 1
- 음의 상관관계 : -1
- 무관 : 0
시간을 고려한 통계치
- 이동 평균
- Moving Average(Rolling Mean)
- 시계열 데이터에서 특정 개수(d) 데이터의 시점(t) 이동을 통해 계산하는 평균
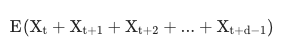
- 이동 표준편차
- Rolling std
- 시계열 데이터에서 특정 개수(d) 데이터의 시점(t) 이동을 통해 계산하는 표준편차(분산 제곱근)
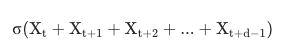
- 자기공분산(Autocovariance)
- 일정 시차(h)를 둔 자기 자신과의 상관계수
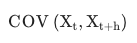
- *자기상관계수(Autocorrelation)
- 일정 시차를 둔 자기 자신과의 상관계수를 의미
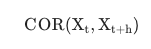
- 일정 시차를 둔 자기 자신과의 상관계수를 의미
- 일정 시차(h)를 둔 자기 자신과의 상관계수
예측이 유의미하려면
직전 5년 치 판매량 : X(t-4), X(t-3), X(t-2), X(t-1), X(t) ➡️ X(t+1) 예측
- t와 무관하게 예측이 맞아떨어져야 함!
- t=2020을 대입해도 -> X(2021)을 정확히 예측해야함
- t와 무관하다
- X(t-h), X(t) : t와 무관하게 h만 달라지는 일정한 상관도를 가져야만 한다는 의미
- 즉, 이동 평균 및 이동 표준편차의 스테이블함이 보장되어야 하는 것
Q. 안정적인 시계열(정상성)은 무엇인지, 변하지 않아야 하는 요소는?
A. 시계열 데이터의 통계적 특성이 변하지 않아야 하는 것을 의미
- 변하지 않아야 하는 요소 : 평균, 분산, 공분산 일정!
- 시간적 요소를 고려한다면 : 이동평균, 이동표준편차, 자기공분산 통계치도 일정!
9-4. 시계열 예측이란(3) 시계열 데이터 사례분석
시계열(Time Series) 생성
- 데이터셋 :
Daily Minimum Temperatures in Melbourne- 온도 변화 관련 시계열 데이터
라이브러리 import
import numpy as np
import pandas as pd
import matplotlib.pyplot as plt
import os
import warnings
warnings.filterwarnings('ignore')데이터셋 로드
dataset_filepath = os.getenv('HOME')+'/aiffel/stock_prediction/data/daily-min-temperatures.csv'
df = pd.read_csv(dataset_filepath)
print(type(df))
df.head()
시계열(Time Series)
- 시간 컬럼을 index로 하는 Series 값
- 현재 데이터셋의 경우 DataFrame으로 변환된 것(아직 시계열 데이터 구조가 아님)
Date 컬럼 index를 통한 시계열 생성
df = pd.read_csv(dataset_filepath, index_col='Date', parse_dates=True)
print(type(df))
df.head()- type은 아직 데이터 프레임
- 시계열
df['Temp']
현재 df는 데이터프레임 형태로 데이터셋을 저장하고 있고, df[Temp]는 Series 형태로 데이터셋을 저장하고 있음
시계열 안정성의 정성적 분석
시각화
- 안정성(Stationarity) 여부
from matplotlib.pylab import rcParams
rcParams['figure.figsize'] = 13, 6
plt.plot(ts1)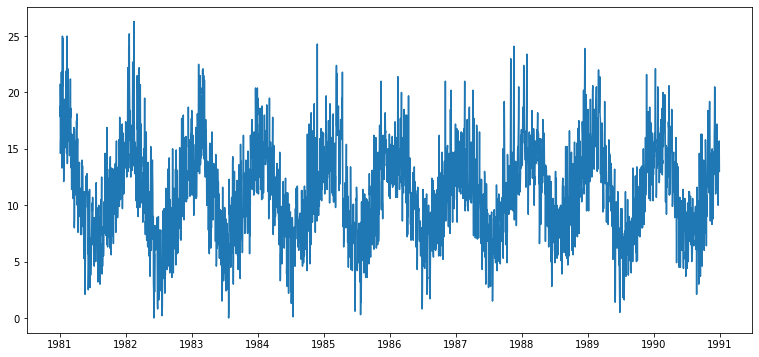
결측치 처리
- 결측치 확인 -> 없음
ts1[ts1.isna()]
참고) 결측치 처리법
- drop : 결측치 데이터 삭제
- interpolate(보간법) : 결측치 양옆 값들로 보간
- extrapolation(보외법) : 범위 밖의 값(외부값)을 예측하여 채우는 것 즉, 주어진 데이터 집합 범위를 넘어가는 영역에서의 값 추정을 위해 사용되는 통계기법(데이터 패턴 및 경향성을 통해 결측치 처리)
- 결측치 보간
ts1=ts1.interpolate(method='time')
print(ts1[ts1.isna()])
plt.plot(ts1)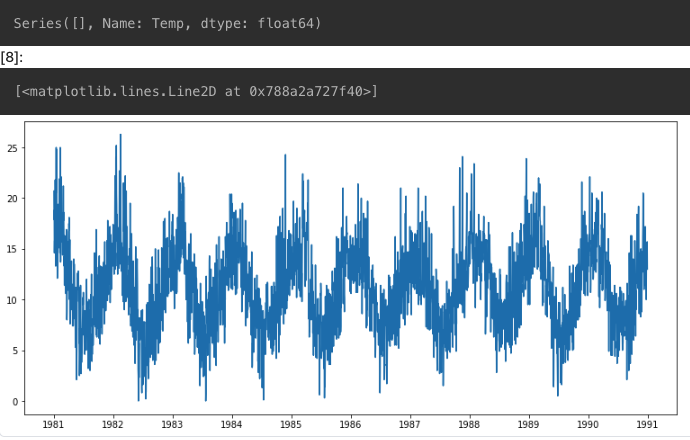
직관적으로 봤을 경우, 평균, 분산, 자기공분산 패턴이 있는 것으로 보임
일정 시간 내 구간 통계치(Rolling Statistics) 시각화
- 현재의 타임 스텝 ~ *window에 주어진 타임 스텝
- *window : 특정 개수(d)
- 이동평균 및 이동 표준편차를 ➡️ 원본 시계열과 같이 시각화해 경향성 확인
- 구간 통계치 함수 정의
def plot_rolling_statistics(timeseries, window=12):
rolmean = timeseries.rolling(window=window).mean() # 이동평균 시계열
rolstd = timeseries.rolling(window=window).std() # 이동표준편차 시계열
# 원본시계열, 이동평균, 이동표준편차 시각화
orig = plt.plot(timeseries, color='blue',label='Original')
mean = plt.plot(rolmean, color='red', label='Rolling Mean')
std = plt.plot(rolstd, color='black', label='Rolling Std')
plt.legend(loc='best')
plt.title('Rolling Mean & Standard Deviation')
plt.show(block=False)- window=12
plot_rolling_statistics(ts1, window=12)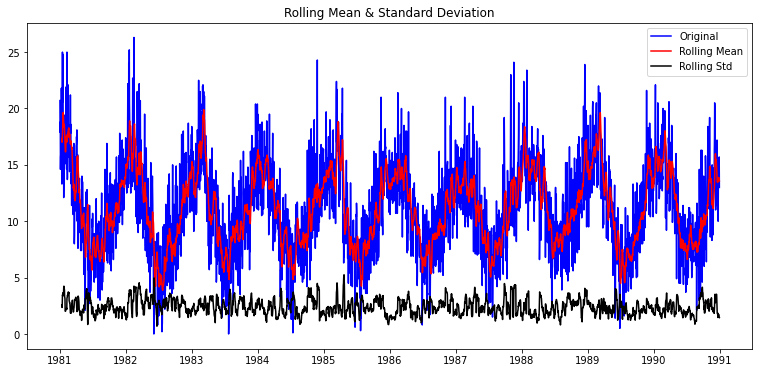
- window=365
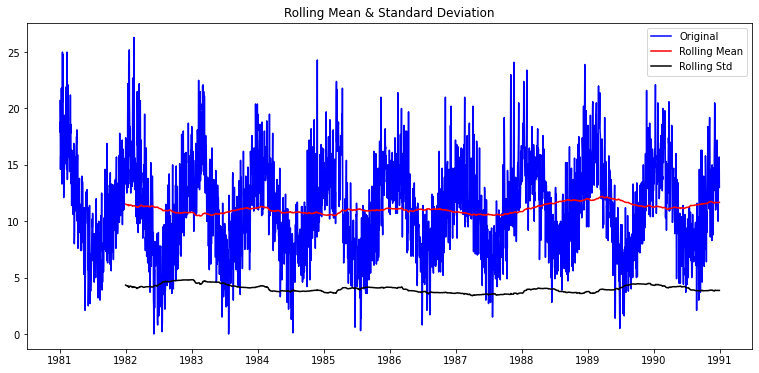
안정성을 보임
타 데이터도 비교해서, 실제로 안정성이 있는 것인지 알아보기
- 데이터셋 :
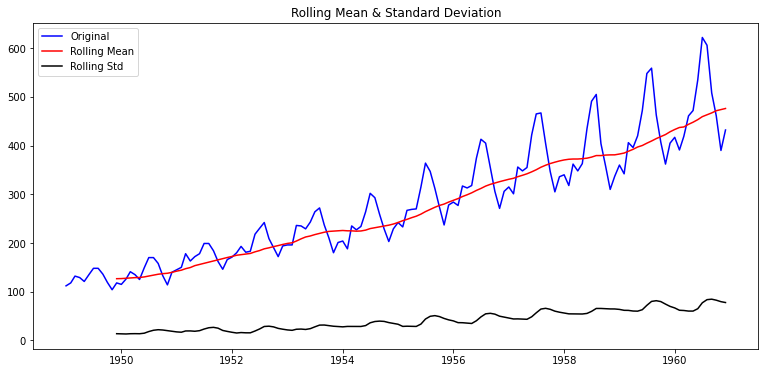
International airline passengers- 시간 추이에 따라 상승 추세가 있음(평균, 분산)
ts2 = df['Passengers']
plt.plot(ts2)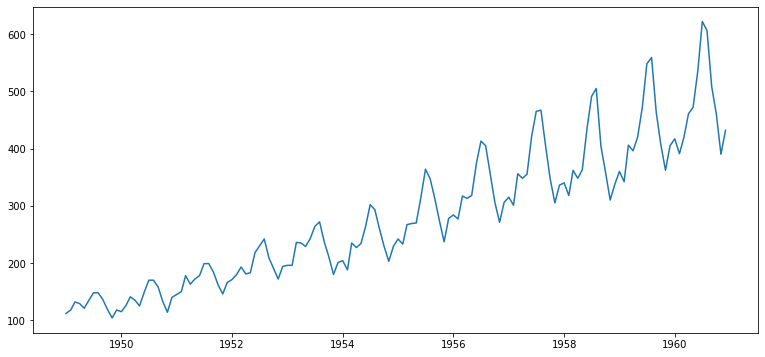
- rolling statistics 함수 적용 후 시각화
- 시간 추이에 따라 평균 및 분산의 상승 추세가 있으므로 안정적이지 않음을 알 수 있음
9-5. 시계열 예측이란(4) Stationary 여부를 체크하는 통계적 방법
ADF Test
- Augmented Dickey-Fuller Test
- 귀무 가설 : 주어진 시계열 데이터가 안정적이지 않다.
- 통계적 가설 검정 과정 ➡️ 귀무 가설 기각 시 대립 가설 채택!
- 정의
- 정상성 판단을 위한 *단위근 검정 방법
- *단위근 : x = 1, y = 1인 해
- 정상성 판단을 위한 *단위근 검정 방법
- 판단 방법
- 귀무가설의 기각을 통해 정상성을 띈다고 해석
- 귀무가설 : 자료에 단위근이 존재한다.
- 대립가설 : 자료에 단위근이 존재하지 않아 시계열 자료가 정상성을 만족한다.
- 귀무가설의 기각을 통해 정상성을 띈다고 해석
- DF 검정의 일반화가 ADF
- DF 검정
- 단위근이 존재한다는 귀무가설의 통계적 검정
- 각 파라미터를 회귀적으로 추정 -> α = 1일 경우 단위근을 가지므로 정상성을 뜨지 않는다고 판별
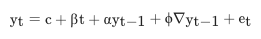
- c : 시계열 데이터 레벨
- β : 추세항
- ADF 검정
- DF 검정 + p lag 차분 추가
- p lag 차분만큼 항이 추가됨
t-p시점까지의 차분 경향성 파악 ➡️ 주기 데이터의 정상성 여부를 판별할 수 있게됨
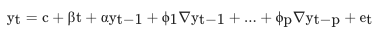
- DF 검정
정상적 시계열 데이터 판별
- 검정 통계량이 Critical Value보다 작다 or p-value가 설정한 유의수준 값보다 작으면 ➡️ 정상적 시계열 데이터로 판별!
- 참고) P-value?
- 귀무가설 가정 시의 확률분포 상에서 현재 관측보다 더 극단적인 관측이 나올 확률
- 귀무가설이 틀렸다고 볼 수 있기도 함
- 0.05 미만으로 낮게 나오면 -> p-value만큼의 오류 가능성 전제로, 귀무 가설의 기각 및 대립가설의 채택 근거가 될 수 있음
statsmodels 패키지와 adfuller 메서드
statsmodels의adfuller이용- 주어진 Time Series에 대한 ADF Test 수행
최적 lag 값은 AIC로 설정
from statsmodels.tsa.stattools import adfuller
def augmented_dickey_fuller_test(timeseries):
dftest = adfuller(timeseries, autolag='AIC')
print('Results of Dickey-Fuller Test:')
dfoutput = pd.Series(dftest[0:4], index=['Test Statistic','p-value','#Lags Used','Number of Observations Used'])
for key,value in dftest[4].items():
dfoutput['Critical Value (%s)' % key] = value
print(dfoutput)ADF Test 수행
- ts1 시계열
- p-value가 0에 가까운 수준으로 아주 작은 값이 나왔기 때문에 귀무가설 기각, 대립가설 채택
대립가설 : 안정적 시계열이다
augmented_dickey_fuller_test(ts1)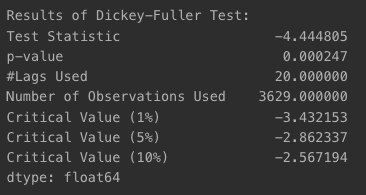
- ts2 시계열
- p-value가 거의 1에 가깝게 나왔기 때문에 귀무가설 기각이 불가능하여 안정적 시계열이라고 말할 수 없어짐
augmented_dickey_fuller_test(ts2)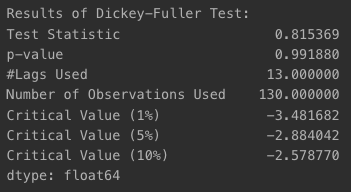
그러나, p-value가 직접적인 근거가 될 수는 없다는 점은 유의해야 함
9-6. 시계열 예측의 기본 아이디어 : Stationary하게 만들 방법은 없을까?
안정적이지 않은 시계열을 안정적인 시계열로 바꾸는 방법
- 정성적 분석 : 기존 시계열 데이터의 가공 및 변형 시도
- 시계열 분해 기법 적용(Time series decomposition)
1. 정성적 분석
1-1. 로그 함수 변환
- 로그 함수 변환
ts_log = np.log(ts2)
plt.plot(ts_log)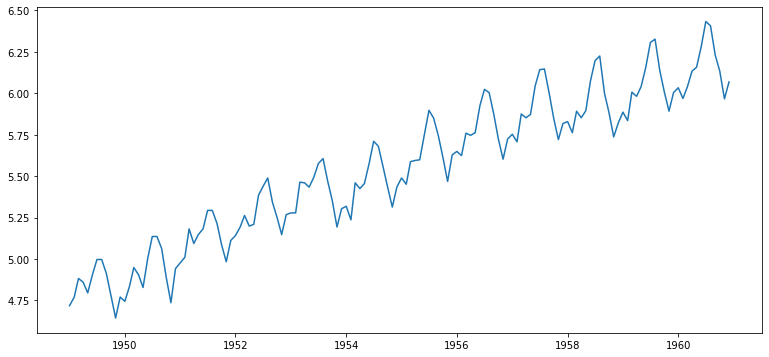
- ADF Test로 로그 변환 효과 확인하기
- p-value가 0.42(이전의 절반 가량 감소)
- 그러나, 여전히 시간 추이에 따라 평균이 계속 증가하는 부분은 남아있음
augmented_dickey_fuller_test(ts_log)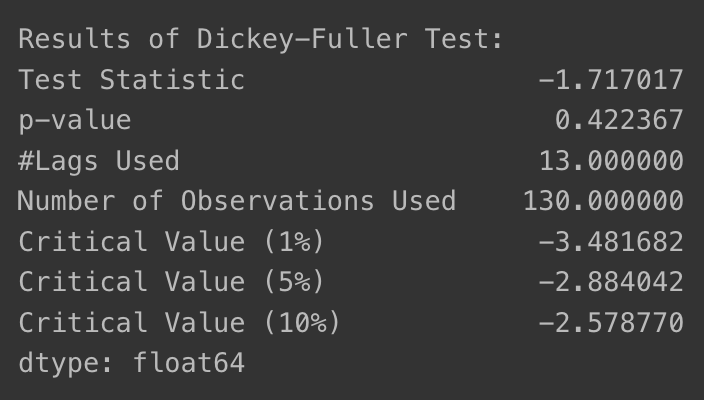
1-2. Moving average 제거 - 추세(Trend) 상쇄
- 변화량 제거
- Moving Average(Rolling mena)을 ts_log에서 빼기
moving_avg = ts_log.rolling(window=12).mean()
plt.plot(ts_log)
plt.plot(moving_avg, color='red')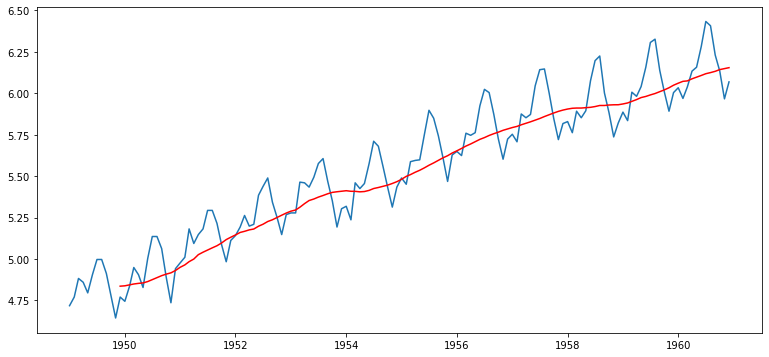
ts_log_moving_avg = ts_log - moving_avg
ts_log_moving_avg.head(15)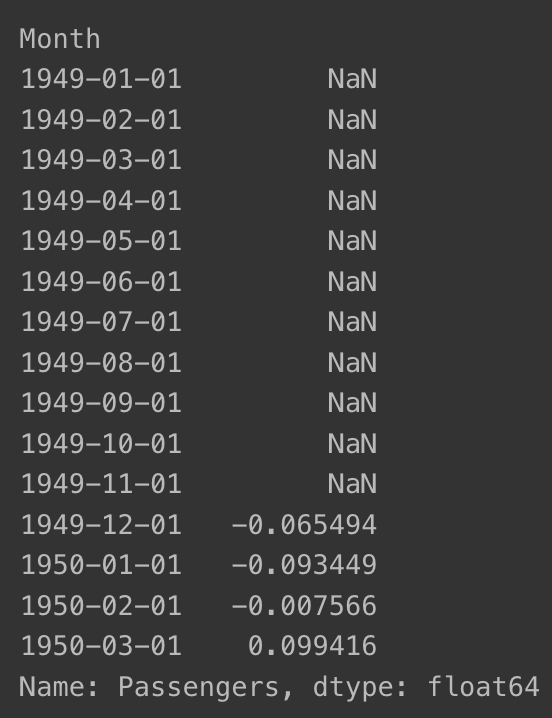
NaN 값은 뭐지?
- Moving Average 계산(windows size=12일 경우) 시 앞의 11개 데이터는 계산이 되지 않음 -> 결측치가 됨
- DF Test시 에러가 되니 제거
- 결측치 제거
ts_log_moving_avg.dropna(inplace=True)
ts_log_moving_avg.head(15)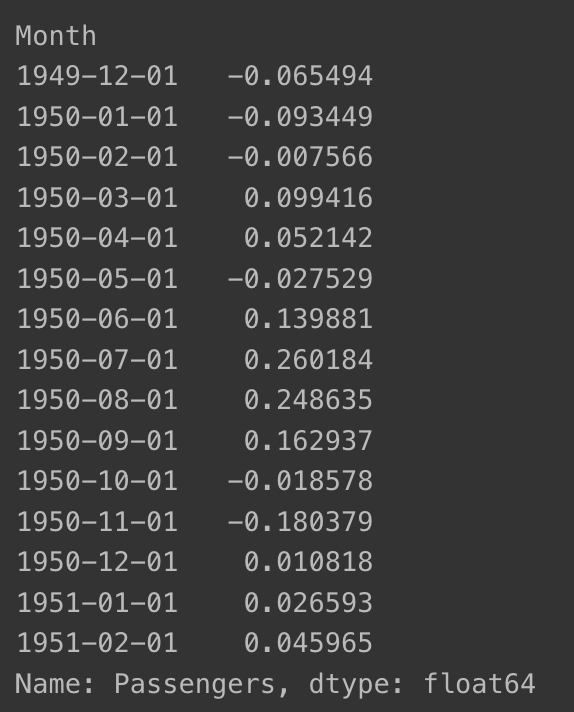
- plot_rolling_statistics
plot_rolling_statistics(ts_log_moving_avg)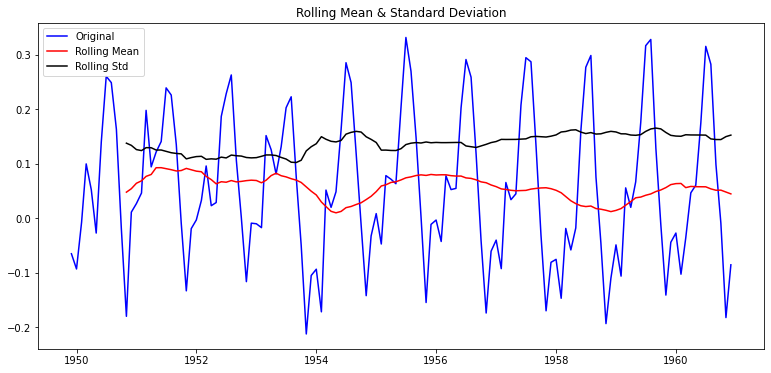
- augmented_dickey_fuller_test
- p-value가 0.02 정도로 아주 낮아짐
- 95% 이상 confidence 즉, 해당 time series는 안정적이라고 볼 수 있음
augmented_dickey_fuller_test(ts_log_moving_avg)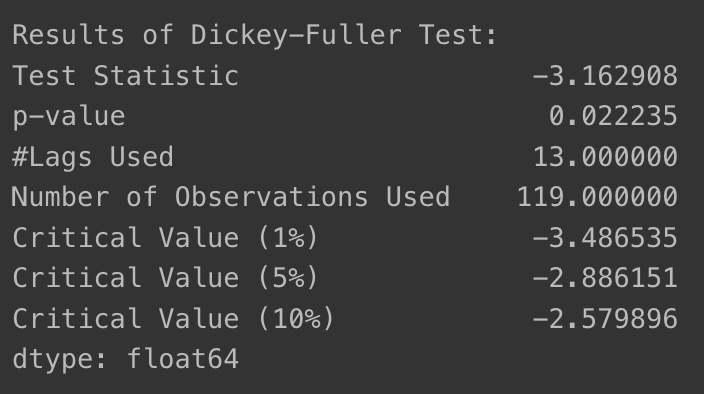
맹점: window 값을 명시해야 한다
- window를 6으로 지정해서 확인해보면 ➡️ 정성적 분석에서는 비슷하다고 느낄 수 있으나, ADF Test의 p-value는 0.18이 되어 안정적 시계열로 판단할 수 없게 됨!
moving_avg_6 = ts_log.rolling(window=6).mean()
ts_log_moving_avg_6 = ts_log - moving_avg_6
ts_log_moving_avg_6.dropna(inplace=True)plot_rolling_statistics(ts_log_moving_avg_6)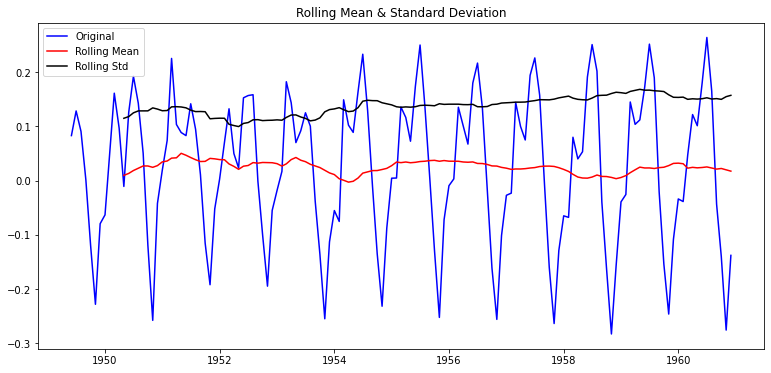
augmented_dickey_fuller_test(ts_log_moving_avg_6)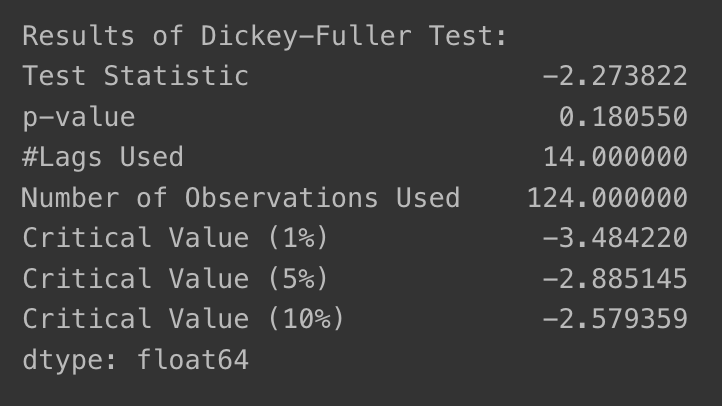
12개월 단위 주기성이 있어 그렇게 판단할 수도 있겠지만, 중요한 부분은 moving average 고려 시 rolling mean을 구하기 위해 window 크기를 결정해야만 한다는 것
1-3. 차분(Differencing)을 통한 계절성(Seasonality) 상쇄
추세(Trend) vs 계절성(Seasonality) vs 주기성(Cycle)
- 추세 (Trend)
- 장기적 증가 or 감소 경향성
- 기울기의 증가 or 감소로 관찰
- 일정 시간 발생(유지되지 않음)
- 계절성(Seasonality)
- 계절 요인 영향으로 1년(일정 기간)안에 반복적으로 나타남 -> 패턴
- 빈도(항상 일정함)
- 주기성(Cycle)
- 정해지지 않은 빈도, 기간동안 일어나는 상승 or 하락
- 패턴 상쇄를 위한 차분(Differencing)
- 시계열을 앞으로 시프트한 시계열 -> 원래 시계열에 빼주는 것
현재 스텝 값 - 직전 스텝 값-> 이번 스텝의 변화량이 됨
- 원본 시계열과 시프트 시계열 그래프
ts_log_moving_avg_shift = ts_log_moving_avg.shift(-1)
plt.plot(ts_log_moving_avg, color='blue')
plt.plot(ts_log_moving_avg_shift, color='green')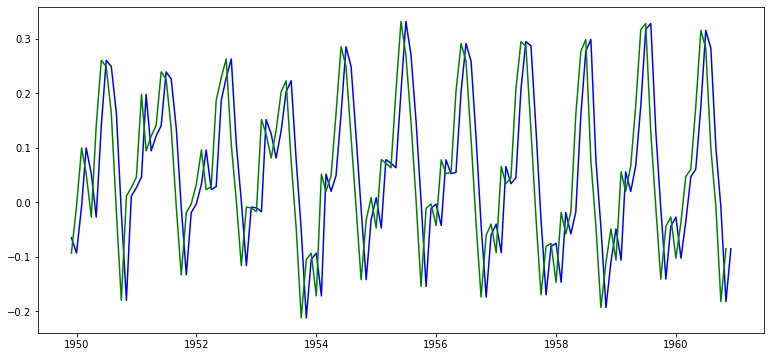
원본 시계열 - 시프트 시계열그래프
ts_log_moving_avg_diff = ts_log_moving_avg - ts_log_moving_avg_shift
ts_log_moving_avg_diff.dropna(inplace=True)
plt.plot(ts_log_moving_avg_diff)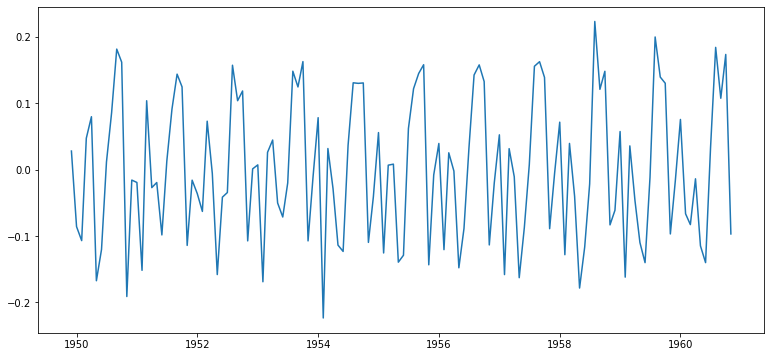
- 안정성 여부 파악
- 이동평균, 이동 표준편차
plot_rolling_statistics(ts_log_moving_avg_diff)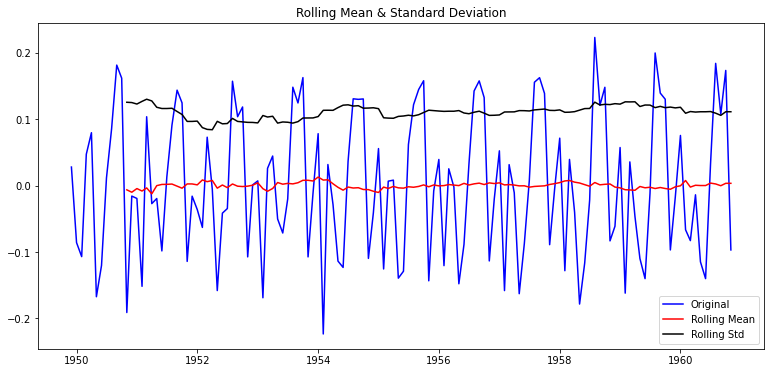
- 차분 적용 후 ADF Test 수행
- 이동 평균 제거를 통해 추세 제거한 시계열 -> 1차 차분 적용해 계절성 상쇄
- p-value: 0.022 ➡️ 0.0019(원래 값의 약 10% 수준으로 줄어듦)
augmented_dickey_fuller_test(ts_log_moving_avg_diff)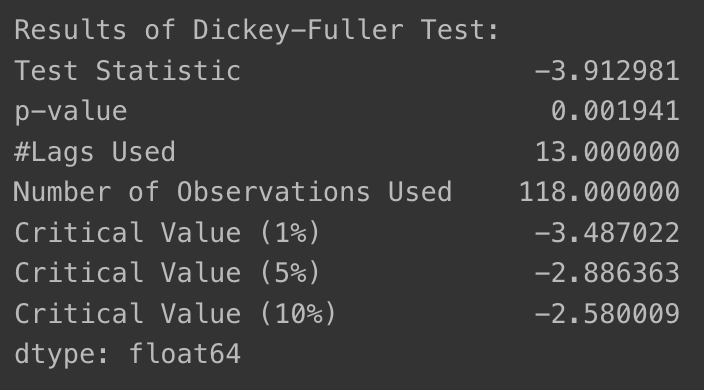
2. 시계열 분해(Time series decomposition)
statsmodels 라이브러리의 seasonal_decompose 사용
- trend, seasonality 분리 기능 존재
- Residual
- 원본 시계열에서 Tread와 Seasonlity 제거 후 나머지
- Trend + Seasonality + Residual = Original 성립
- Residual
from statsmodels.tsa.seasonal import seasonal_decompose
decomposition = seasonal_decompose(ts_log)
trend = decomposition.trend # 추세
seasonal = decomposition.seasonal # 계절성
residual = decomposition.resid # 로그변환 - 추세 - 계절성
plt.rcParams["figure.figsize"] = (11,6)
plt.subplot(411)
plt.plot(ts_log, label='Original')
plt.legend(loc='best')
plt.subplot(412)
plt.plot(trend, label='Trend')
plt.legend(loc='best')
plt.subplot(413)
plt.plot(seasonal,label='Seasonality')
plt.legend(loc='best')
plt.subplot(414)
plt.plot(residual, label='Residuals')
plt.legend(loc='best')
plt.tight_layout()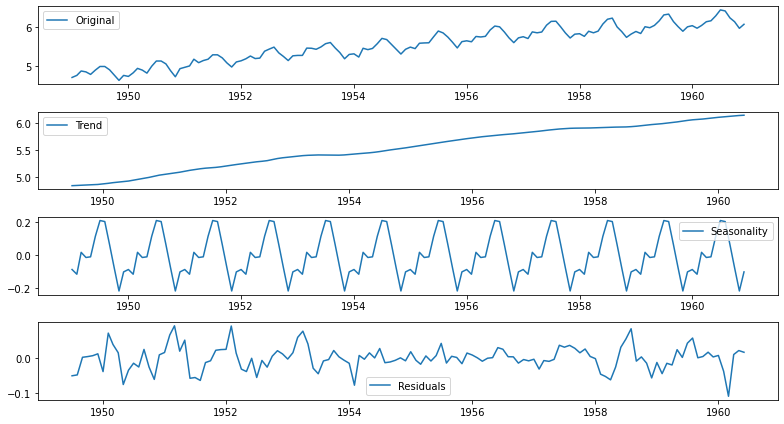
Residual에 대한 안정성 여부 파악
plt.rcParams["figure.figsize"] = (13,6)
plot_rolling_statistics(residual)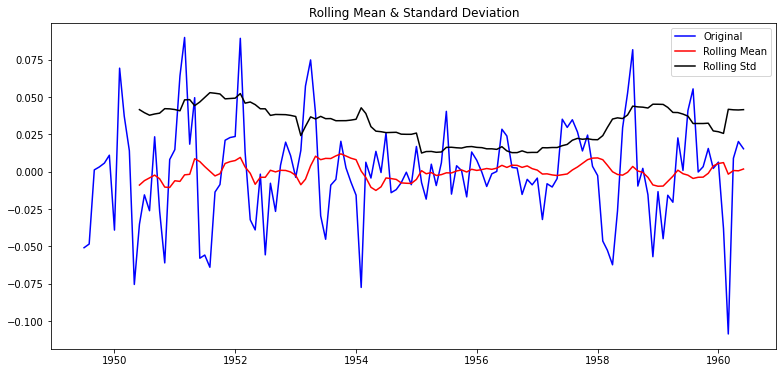
residual.dropna(inplace=True)
augmented_dickey_fuller_test(residual)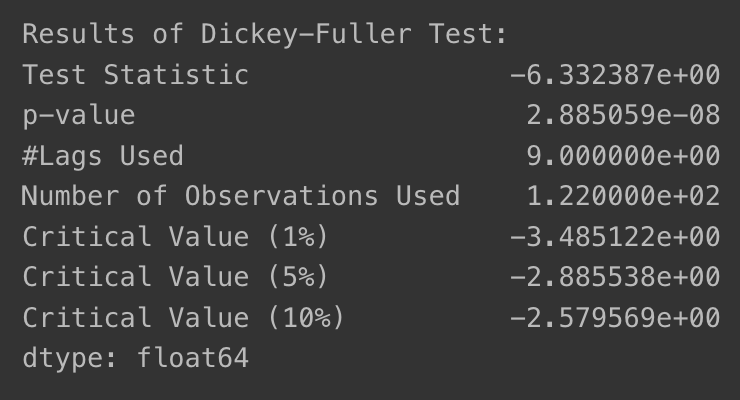
- p-value가 0.00000002885059 수준으로 아주 작게 나옴 -> 안정적 시계열로 볼 수 있게 됨
9-7. ARIMA 모델의 개념
ARIMA 모델 정의
- AR(Autoregressive) + I(Integrated) + MA(Moving Average)
AR
- 자기회귀(Autoregressive)
- 과거 값 회귀를 이용한 미래 값 예측
- 가 이전 p개의 데이터() 가중합으로 수렴
- 시계열의
Residual부분을 모델링 - 가중치 크기가 1보다 작은 의 가중합으로 수렴하는 자기 회귀 모델 == 안정적 시계열(동치)
- 주식값이 항상 일정하게 균형적인 수준 유지를 보인다는 것을 예측하는 것
MA
- 이동평균(Moving Arerage)
- 가 이전 q개 예측 오차값의 가중합으로 수렴
- 시계열의
Trend부분을 모델링 - 예측 오차값(e_{t-1]) > 0 => 모델 예측보다 관측값이 더 높음 -> 다음 예측시부터 예측치를 올려서 잡게 됨
- 주식값이 최근 증감 패턴 유지를 보일 것이라 보는 관점
I
- 차분 누적(Integration)
- 가 이전 데이터 및 d차 차분의 누적합이라고 봄
- 시계열의
Seasonality부분을 모델링
AR 형태의 기대와 MA 형태의 우려 속에서 적정 수준을 찾는 것이 ARIMA
ARIMA 모델 파라미터: p, q, d
- p : AR의 시차
- d : 차분 누적 함수(I)
- q : MA의 시차
- 일반적 사용 ➡️ p와 q 중 하나는 0이라는 것
- 시계열 데이터는 AR 혹은 MA 중 1가지 경향을 두드러지게 가지는 경우가 많기 때문
- p + q < 2
- p * q = 0
-
파라미터 선정 방법
- ACF(Autocorrelation Function)
- lag(시차)에 따른 관측치 사이 관련성 측정
- 시계열 현재 값이 과거 값과 어떤 상관이 있는지 파악
- ACF plot의 x축은 상관계수, y축은 시차 수
- PACF(Partial Autocorrelation Function)
- 다른 관측치 영향 배제 ➡️ 두 시차 관측치 간 관련성만 측정
- k 이외 시차를 갖는 관측치 배제
- 특정 두 관측치 및 의 관련 정도의 척도
Q. ACF와 PACF를 사용해 어떤 정보를 파악할 수 있는지?
A. 시계열 데이터 상관관계 패턴 파악, 유의한 시차의 식별 및 파라미터의 결정에 도움을 줌
- ACF(Autocorrelation Function)
ACF Plot, PACF Plot
- ACF ➡️ MA 모델의 시차 q 결정
- PACF ➡️ AR 모델의 시차 p 결정
from statsmodels.graphics.tsaplots import plot_acf, plot_pacf
plot_acf(ts_log)
plot_pacf(ts_log)
plt.show()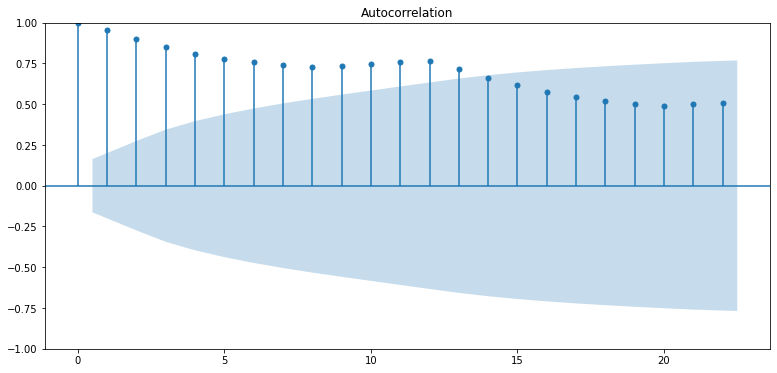
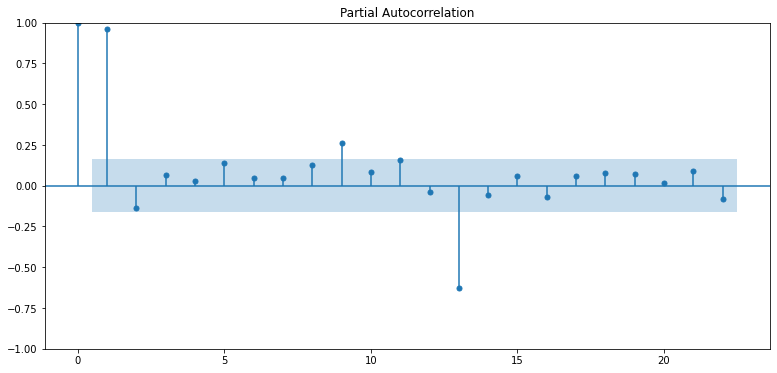
- 결과 보기
- PACF
p=1이 적합해 보임(∵ p가 2 이상인 구간에서 pacf는 0에 가까워지고 있음)- 상관도가 0이니 고려할 필요가 없다는 의미인 것
- ACF
- 점차 감소 -> AR(1) 모델 유사 형태
- q는 적합 값이 없는 것으로 판단
- MA를 고려하지 않는다면 -> q=0으로 둘 수도 있지만, 대부분은 q를 바꿔서 넣으며 확인함!
- PACF
참고) AR/MA 모형과 ACF/PACF 관계
AR(p) MA(q) ACF 점차 감소 시차 q 이후 0 PACF 시차 p 이후 0 점차 감소
d차 차분을 통한 시계열 안정 상태 확인
- 1차 차분
- 명확하게 안정적이라고 보기는 아직 어려움
diff_1 = ts_log.diff(periods=1).iloc[1:]
diff_1.plot(title='Difference 1st')
augmented_dickey_fuller_test(diff_1)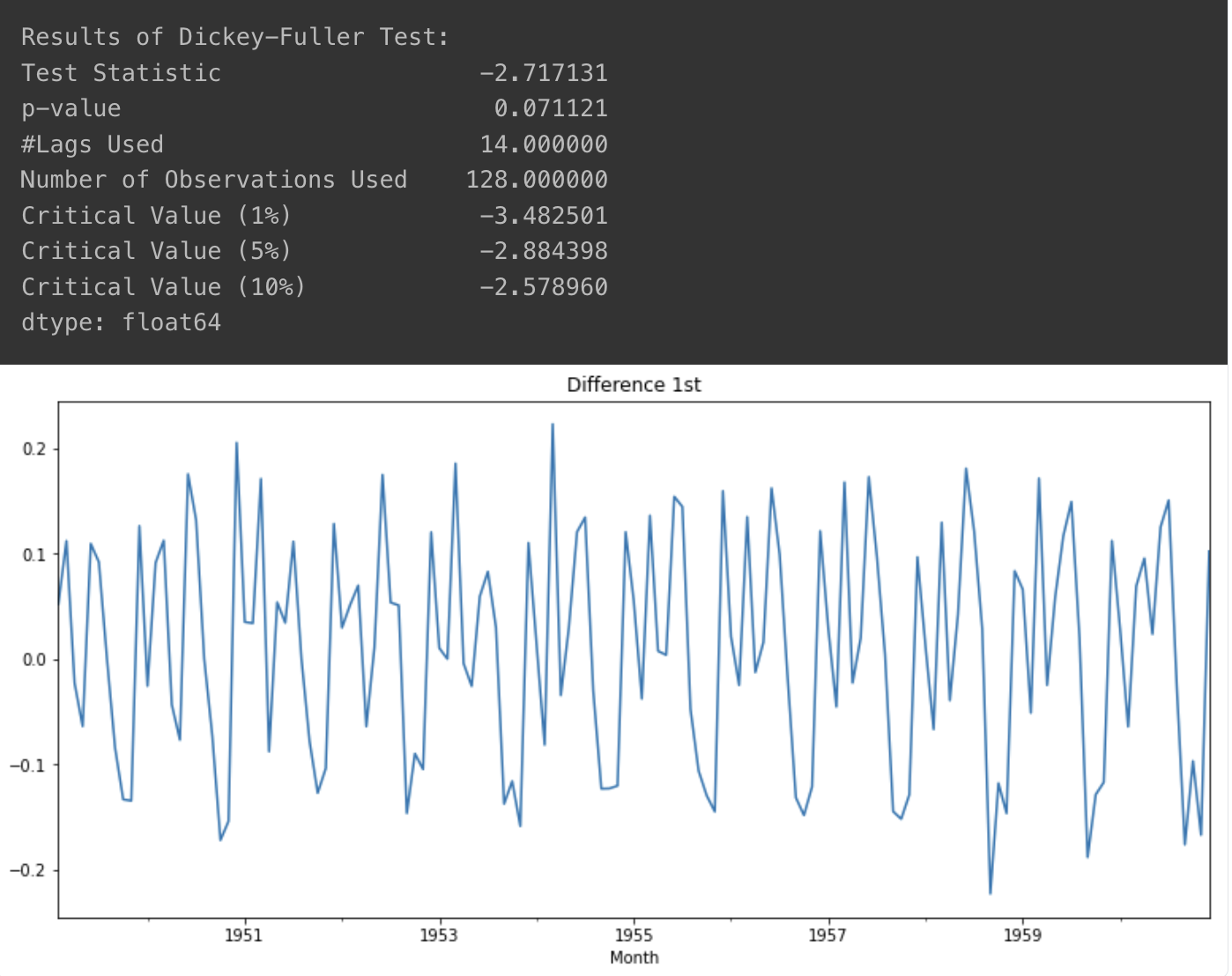
- 2차 차분
- 1차 차분보다 더 안정적이긴 하지만, 1차 차분도 사용해볼 여지가 있음
- 이 값도 바꿔가며 찾아보는 것이 좋을 것 같음
diff_2 = diff_1.diff(periods=1).iloc[1:]
diff_2.plot(title='Difference 2nd')
augmented_dickey_fuller_test(diff_2)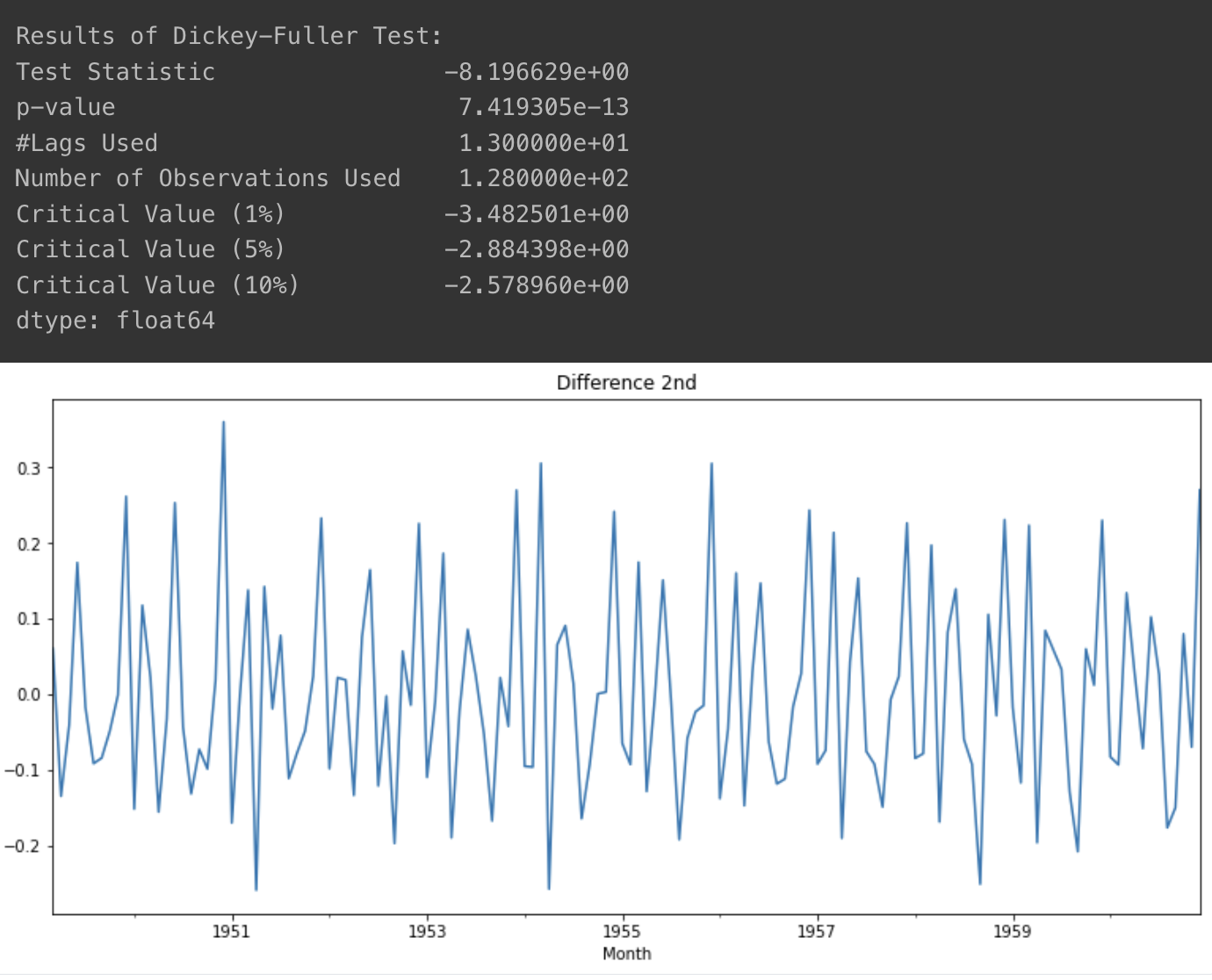
학습 데이터 분리
- 비율은 9:1로 설정(학습:테스트)
- 잘 이어져 있음을 확인할 수 있음
train_data, test_data = ts_log[:int(len(ts_log)*0.9)], ts_log[int(len(ts_log)*0.9):]
plt.figure(figsize=(10,6))
plt.grid(True)
plt.plot(ts_log, c='r', label='training dataset')
plt.plot(test_data, c='b', label='test dataset')
plt.legend()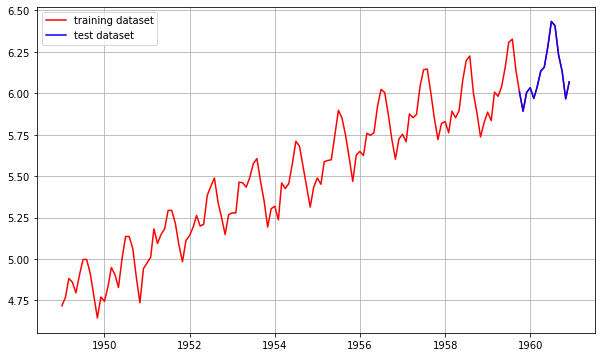
- 데이터셋 형태 확인
print(ts_log[:2])
print(train_data.shape)
print(test_data.shape)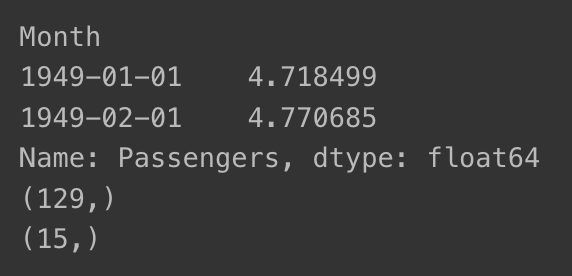
9-8. ARIMA 모델 훈련과 추론
모델 훈련
import warnings
warnings.filterwarnings('ignore')
from statsmodels.tsa.arima.model import ARIMA
model = ARIMA(train_data, order=(14, 1, 0))
fitted_m = model.fit()
print(fitted_m.summary())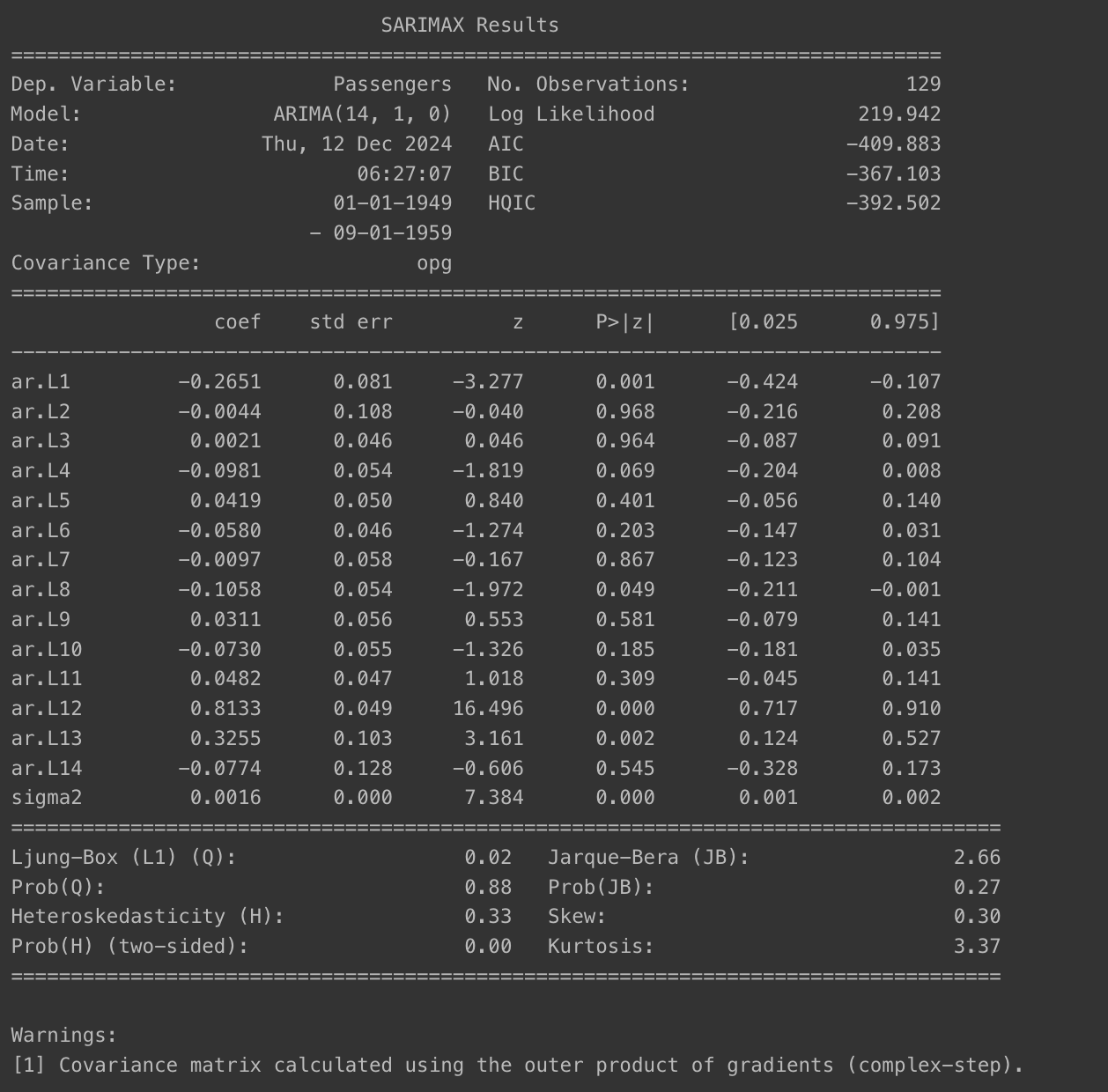
- 결과 시각화
fitted_m = fitted_m.predict()
fitted_m = fitted_m.drop(fitted_m.index[0])
plt.plot(fitted_m, label='predict')
plt.plot(train_data, label='train_data')
plt.legend()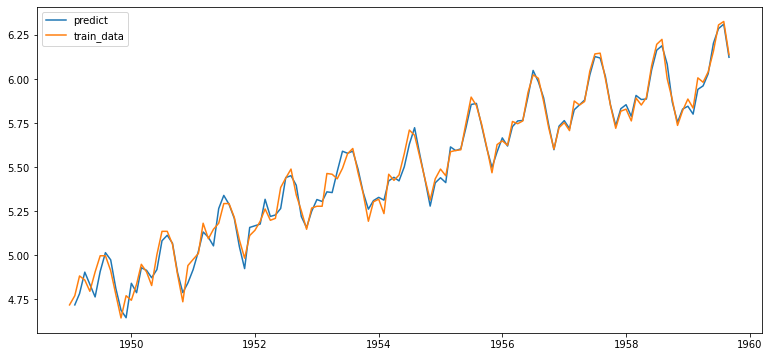
forecast()- 테스트 데이터 구간의 데이터 예측 : 비교적 잘 예측했음을 알 수 있음
model = ARIMA(train_data, order=(14, 1, 0))
fitted_m = model.fit()
fc= fitted_m.forecast(len(test_data), alpha=0.05)
fc_series = pd.Series(fc, index=test_data.index)
plt.figure(figsize=(9,5), dpi=100)
plt.plot(train_data, label='training')
plt.plot(test_data, c='b', label='actual price')
plt.plot(fc_series, c='r',label='predicted price')
plt.legend()
plt.show()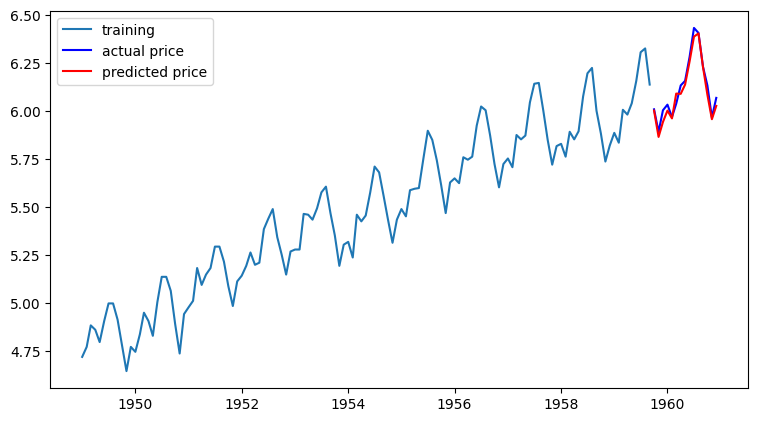
- MSE, MAE, RMSE, MAPE 계산
- np.exp()로 지수 변환한 후 정확한 오차 계산
- MSE : 평균 제곱 오차
- MAE : 평균 절대 오차
- RMSE : 평균 제곱근 오차
- MAPE : 평균 절대 백분율 오차
- np.exp()로 지수 변환한 후 정확한 오차 계산
from sklearn.metrics import mean_squared_error, mean_absolute_error
import math
mse = mean_squared_error(np.exp(test_data), np.exp(fc))
print('MSE: ', mse)
mae = mean_absolute_error(np.exp(test_data), np.exp(fc))
print('MAE: ', mae)
rmse = math.sqrt(mean_squared_error(np.exp(test_data), np.exp(fc)))
print('RMSE: ', rmse)
mape = np.mean(np.abs(np.exp(fc) - np.exp(test_data))/np.abs(np.exp(test_data)))
print('MAPE: {:.2f}%'.format(mape*100))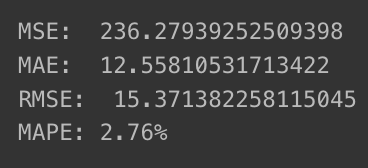
MAPE 기준 5% 이내이기 때문에 매우 좋은 모델로 평가됨