[Image Processing] Lecture 03 - Histogram

1. Histogram

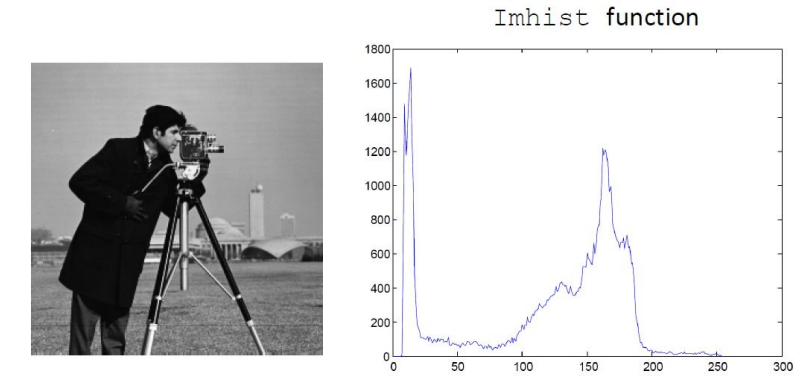
• Histogram : 이미지의 밝기 분포(픽셀 값)를 시각적으로 나타내는 것이다. 이는 이미지의 대비, 밝기, 명암비 등을 분석하는 핵심적 도구이다.

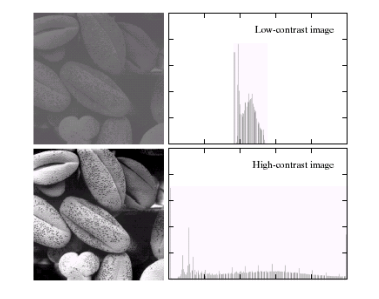
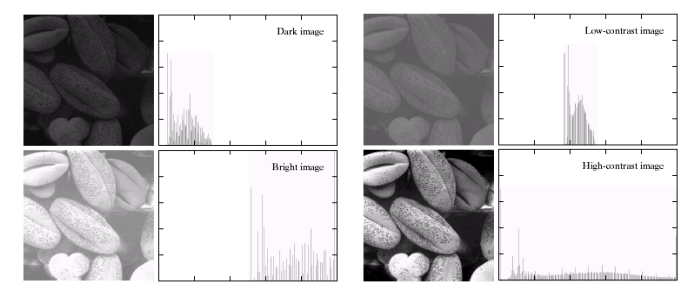
  • 그래프가 한쪽에 몰려있는 경우 : 대비가 낮은 이미지이다.

  • 그래프가 고르게 분포하는 경우 : 대비가 높은 이미지이다.

  • 대비가 높은 이미지는 히스토그램의 분포가 고르다. 따라서 히스토그램 분포가 고를수록 이미지의 디테일이 더 잘 드러난다고 볼 수 있다.

1-1. Histogram Stretching

• Histogram Stretching : 히스토그램을 넓게 분포시켜, 대비를 상승시키는 기법이다.

  • 예제

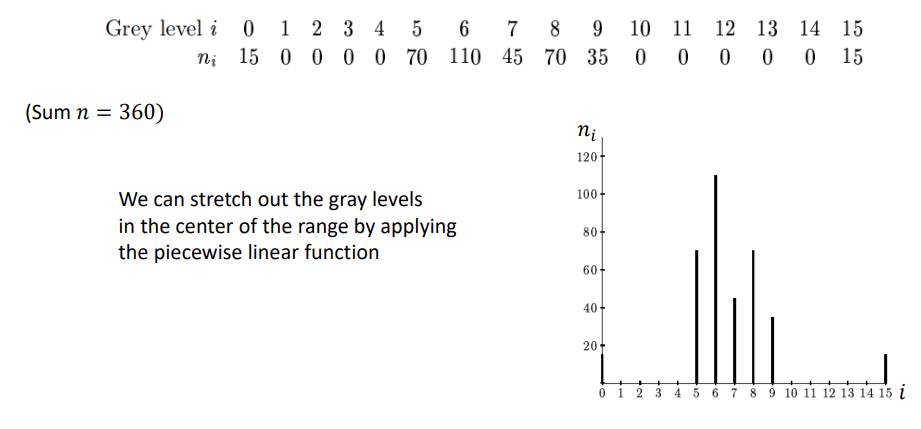
    • 위와 같은 경우, 픽셀이 중간에 몰려있으므로 대비가 낮은 이미지이다.
      

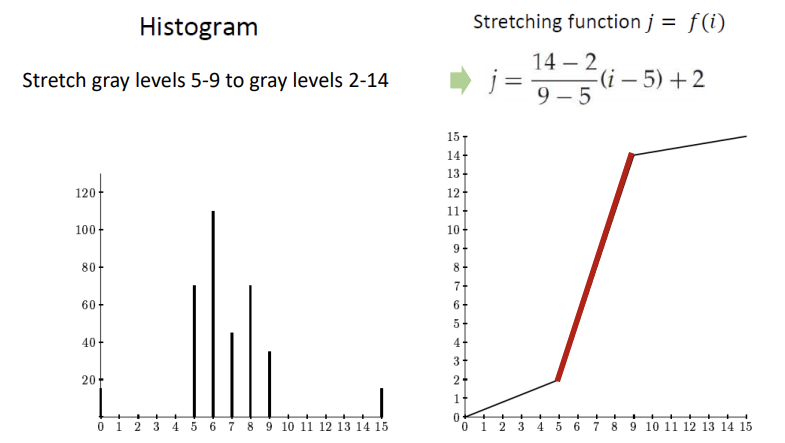
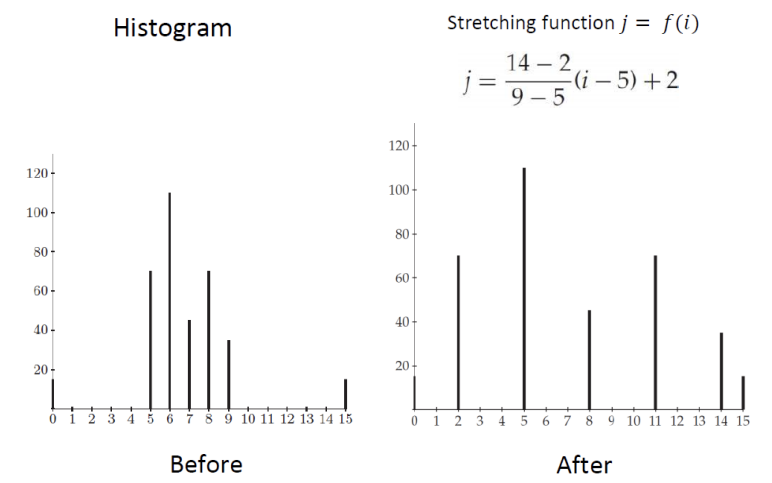
    • 이 히스토그램을 넓게 펼친다는 것은, 5~9 사이에 있는 값들을 고르게 분포시킨다는 것이다.

    • 5~9 사이의 값들을 2~14의 값들로 Linear하게 펼친 결과는 다음과 같다.
      

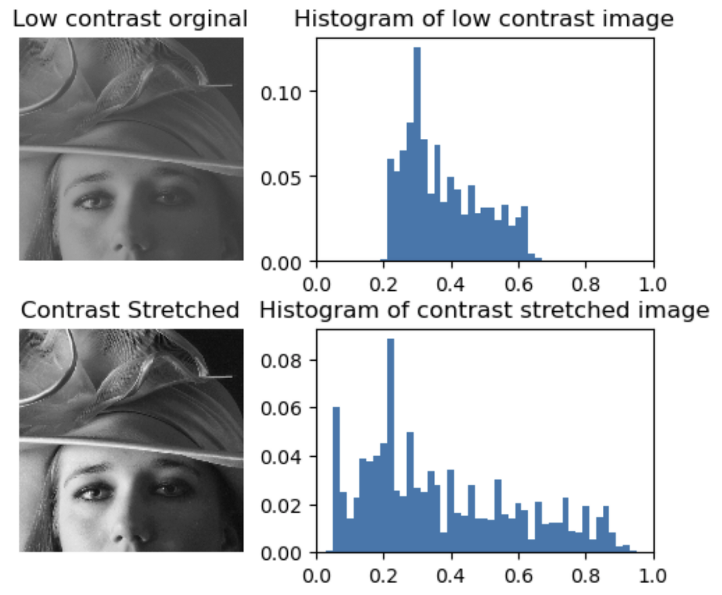
    • 원본 히스토그램의 픽셀 값들을 특정 방법(위 경우 Linear 함수를 사용)으로 넓게 분포시키는 것이 히스토그램 스트레칭이다.

• Piecewise linear stretching function : 두 끝 점을 정의하면, 해당 점 사이에 존재하는 값들은 전부 Linear 함수에 의해 결정된다.

  $(input)\,\,Gray Level (a_i - a_{i+1})\,\rarr\,(output)\,\,Gray Level (b_i - b_{i+1}) \\ y = \frac{b_{i+1} - b_i}{a_{i+1} - a_i}(x-a_i) + b_i$
  • 주어진 구간 $(a_i, a_{i+1})$의 입력 그레이 레벨을 $(b_i, b_{i+1})$의 출력 그레이 레벨로 선형적 매핑한다.

1-2. Histogram Equalization

• Histogram Equalization : 히스토그램 평활화는 입력 이미지의 Gray Level 분포를 가능한 한 균일하게 만드는 것이다. 이는 이미지의 전체적인 대비를 향상시키고, 더 많은 디테일들을 명확하게 볼 수 있도록 돕는다.

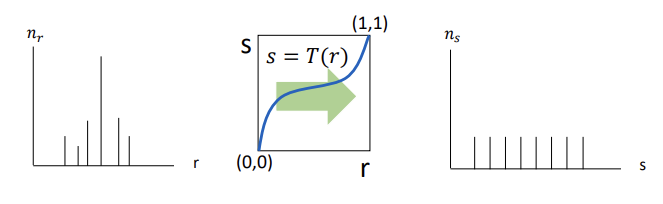
  • Ideal case : 이산적인 값을 갖는 입력 이미지에 특정 함수를 적용한 계산 결과, Gray Level을 완전 균등하게 분포시킨다.

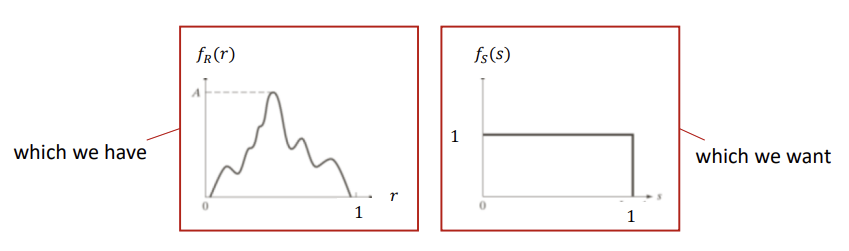
  • Continuous case : 연속적인 값을 갖는 이미지의 경우, 히스토그램을 확률 밀도 함수(PDF)로 만들어 이 함수를 정규화함으로써 히스토그램 평활화를 진행한다.

    • 위와 같은 경우, $f_R(r)$의 히스토그램 평활화의 결과로 $f_S(s)$가 된 것이다.

    • 이때, $s$의 정의역은 $T(r)$이다.

    • 결론적으로, $f_R(r)ds = f_S(s)ds$이다. 즉, 두 함수의 넓이는 동일하다.

    • 따라서 우리는 아래 식을 유도할 수 있는 것이다.

• 히스토그램 평활화 비교

  • 입력 이미지가 연속적인 값을 갖는 경우

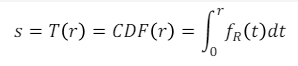
  • 입력 이미지가 이산적인 값을 갖는 경우

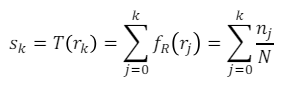
• 히스토그램 평활화 과정

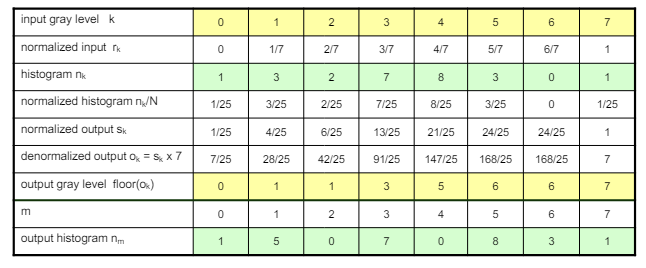
  1). 히스토그램을 구한다.

  2). 히스토그램을 총 픽셀수로 나눈다.

  3). 누적 분포(CDF)를 구한다.

  4). 누적 시킨 값에 gray level의 최댓값(255)를 곱한다.

  5). 반올림 또는 버림을 통해 정수값으로 변환한다.

  6). 구해진 정수값을 히스토그램 평활화 결과로 반환한다.

1-3. Histogram Stretching vs Histogram Equalization

• 히스토그램 스트레칭 : 이미지의 히스토그램을 확장하여 픽셀 값이 0 ~ 255의 범위 전체에 분포하도록 조정하는 기법이다.

  • 이미지의 명암비를 개선하기 위한 목적.

  • 입력 이미지의 최소 및 최대 픽셀 값을 찾아 이 값을 이용해 명암 범위를 재조정

  • 사람이 수동으로 계산을 해야한다.

• 히스토그램 평활화 : 이미지의 히스토그램을 평탄하게 만들어, 모든 픽셀 값이 가능한 한 동일한 빈도로 분포하도록 조정하는 기법.

  • 이미지의 명암비를 극대화하여 더 많은 디테일을 드러내기 위한 목적

  • 이미지의 누적 분포 함수(CDF)를 이용하여 픽셀 값을 다시 매핑

  • 자동으로 계산을 적용할 수 있다.

  • 완벽하게 Uniform한 결과는 거의 얻기 힘들다.