[Image Processing] Lecture 04 - Image Filtering

이한량·2024년 5월 30일

Image Processing

목록 보기

3/12

1. Linear Filtering

Linear Filter : 선형 필터는 이미지 $f$ 와 필터(커널, 마스크) $w$ 사이의 곱셈 합 연산을 수행한다.
- 커널 $w$ 는 연산 대상의 이웃을 정의하는 크기의 배열, 계수는 필터의 성격을 결정한다.
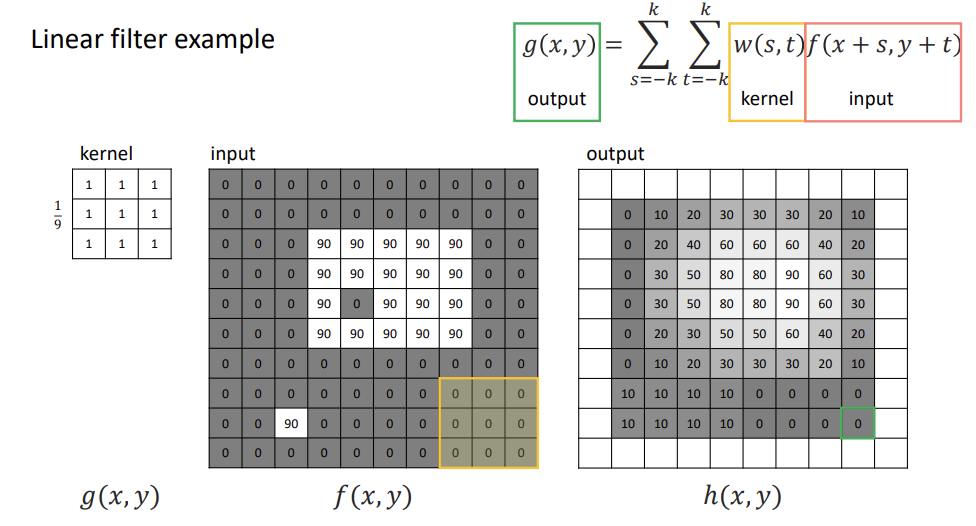
- 선형 필터의 수학적 표현
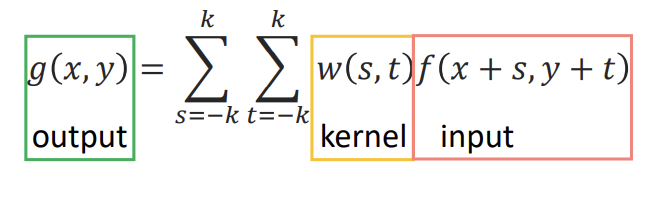
- 위 경우 커널의 크기 = $(2k+1) * (2k+1)$
예시
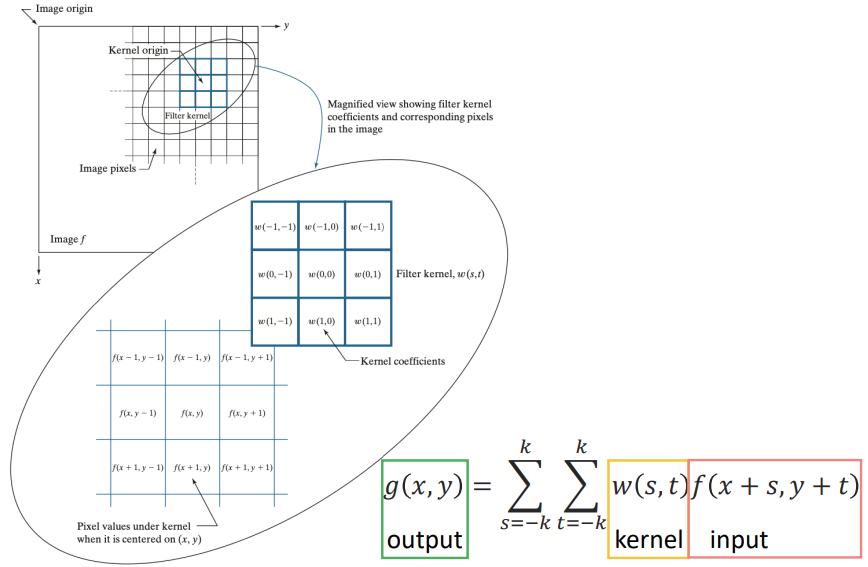
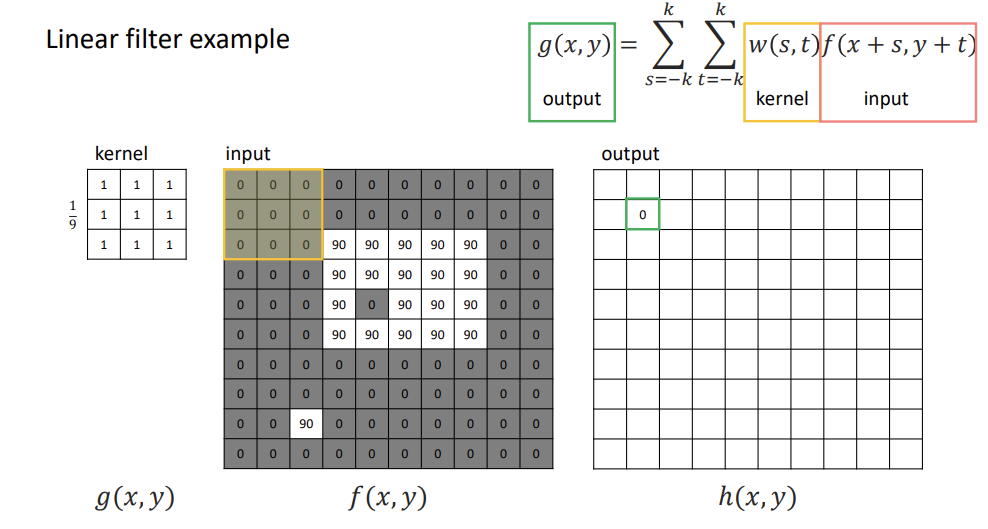
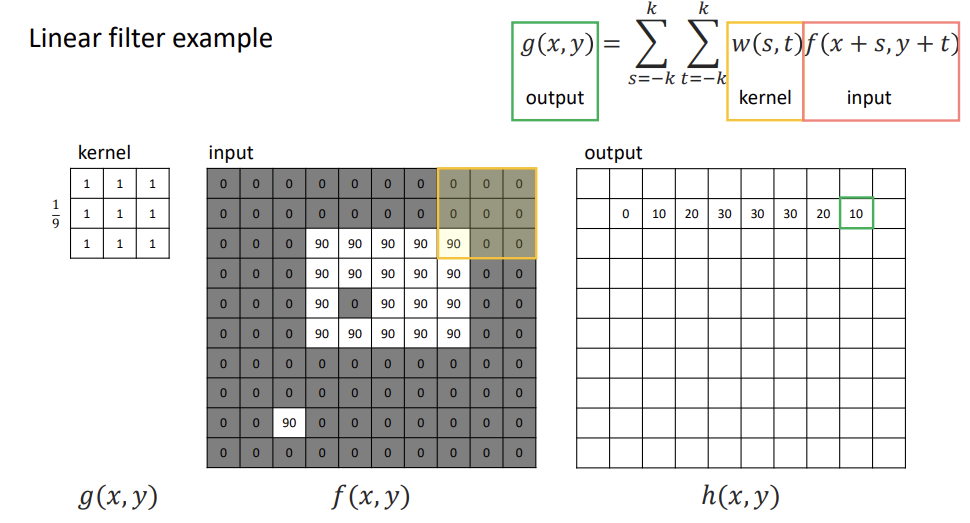
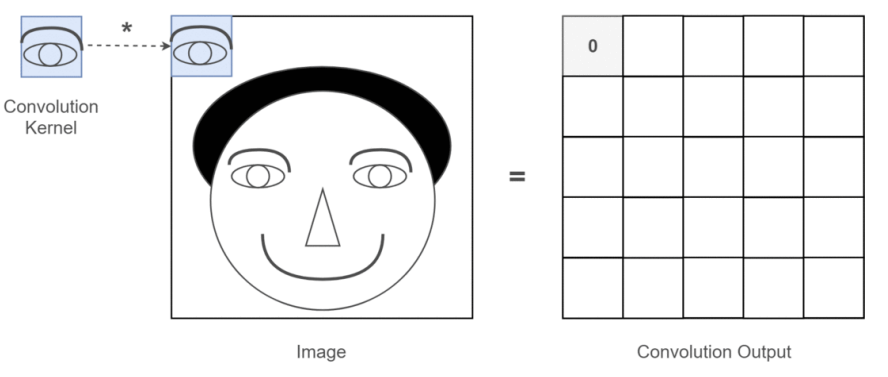
선형 필터의 중요한 특징 : 특정 지역의 패턴이 필터와 유사할수록 필터링의 반응성이 커지고, 일치할 때 최대가 된다.
- 필터는 특정 패턴, 질감, 방향성을 민감하게 감지하도록 설계될 수 있다.
- 결론적으로, 선형 필터를 적절히 설계하는 것은 이미지를 분석하는 데 매우 중요한 도구라는 것을 알 수 있다.
선형 필터링의 비용
- 주어진 이미지의 크기 : n * n
- 필터의 크기 : m * m
- 각 픽셀 (x,y)에 대해 필터링을 적용할 때, m * m의 곱셈 연산이 필요하다.
- 전체 픽셀에 대해 이 연산을 수행하므로, 계산 비용은 다음과 같다.
  $all\,pixels * kernel\,size = n^2 * m^2$
Boundary effect : 이미지의 가장자리 부근에서 선형 필터링을 진행할 때, 필터가 이미지의 가장자리를 벗어나는 문제가 발생한다.
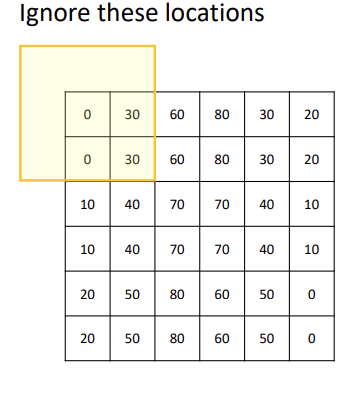
이에 대한 해결책들은 다음과 같다.
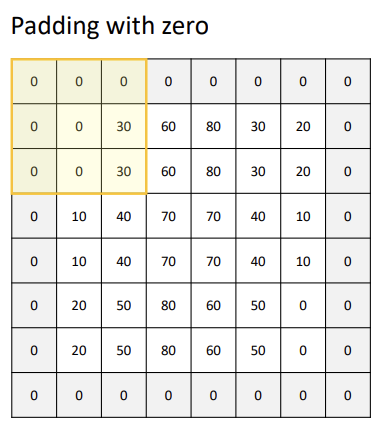
- Padding with zero : 이미지의 가장자리 벗어난 부분을 픽셀 0으로 채운다. 가장 간단한 방법이지만, 이미지의 가장자리에서 필터의 값이 변형될 수 있다.
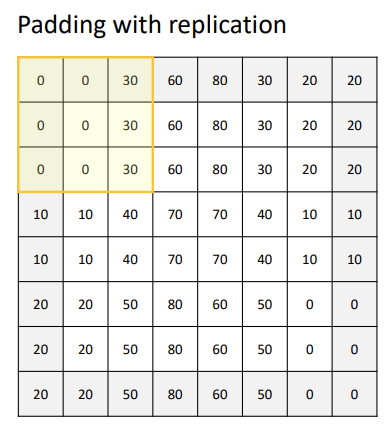
- Padding with replication : 가장자리 픽셀을 복제하여 벗어난 부분을 채운다. 이 방법은 이미지의 가장자리 정보를 유지하므로 가장자리의 필터 값 변형을 최소화 한다.
- Padding with reflection : 이미지의 가장자리를 반사시켜 확장하는 방법이다.
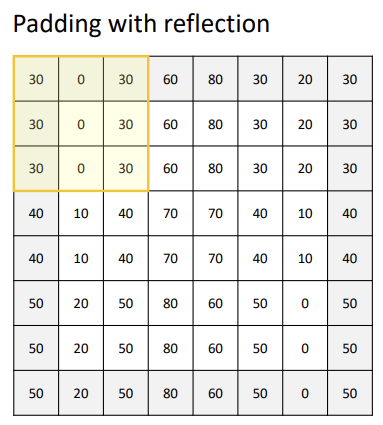
Correlation and Convolution
- Correlation (상관 관계)
  - 필터를 이미지의 각 위치에 대응시켜 곱한 후 결과를 합하는 연산을 수행함.
- Convolution (컨볼루션)
  - 이미지 위에서 이동시키며 대응되는 위치에 대한 값을 곱한 뒤 합하여 연산하는 것은 Correlation과 유사
  - 필터를 180도 회전시켜 사용하므로 계산 방식에서 차이가 있음.
  - Convolution은 교환 법칙, 결합 법칙, 분배 법칙이 모두 성립하므로 대부분의 필터링에서 사용되는 매우 중요한 연산이다.
선형 필터의 특성
- Additivity (가산성) : 선형 필터 $w_1, w_2$ 가 있을 때, 두 필터의 합으로 구성된 필터를 이미지 $f$ 에 적용한 결과는 각 필터를 $f$ 에 적용한 결과의 합과 동일하다.
  $(w_1 + w_2) * f(x,y) = w_1 * f(x,y) + w_2 * f(x,y)$
- Homogeneity (동질성) : 선형 필터 $w$ 와 스칼라 $k$ 에 대해서, $k$ 와 $w$ 의 곱으로 구성된 필터를 이미지 $f$ 에 적용한 결과는 필터 $w$ 를 $kf$ 에 적용한 결과와 동일하다.
  $(kw) * f(x,y) = w * (kf(x,y))$
- Shift invariance (시프트 불변성) : Output은 절대 위치에 의존하지 않는다. 즉, 이미지 내의 객체가 어디에 위치하든 간에 객체를 동일하게 인식하고 처리할 수 있다는 것이다.

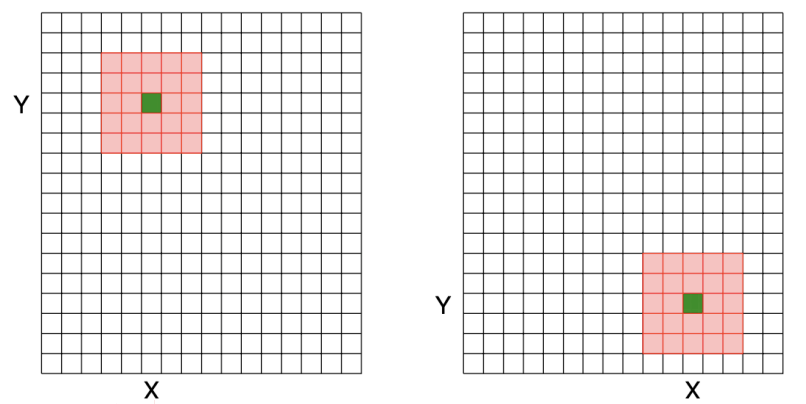
2. Smoothing

Smoothing : 이미지의 픽셀 값을 주변 값들과 섞어 픽셀 값의 경계가 모호해지고, 뭉개지도록 만드는 기법이다.
- 튀는 값들을 없애는 효과가 있어, 이미지의 Noise를 제거하는 데 사용되기도 한다.
- 경계선을 흐리게 만들어 이미지를 부드럽게 만든다.

2-1. Average Filter

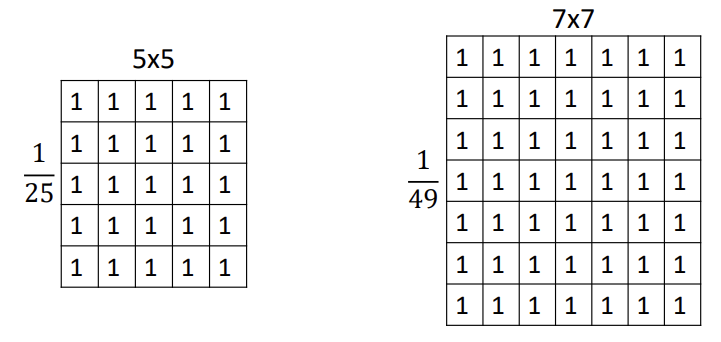
Average Filter : 평균 필터는 이미지의 각 픽셀을 그 주변 픽셀 값들의 평균 값으로 대체하는 방식이다.
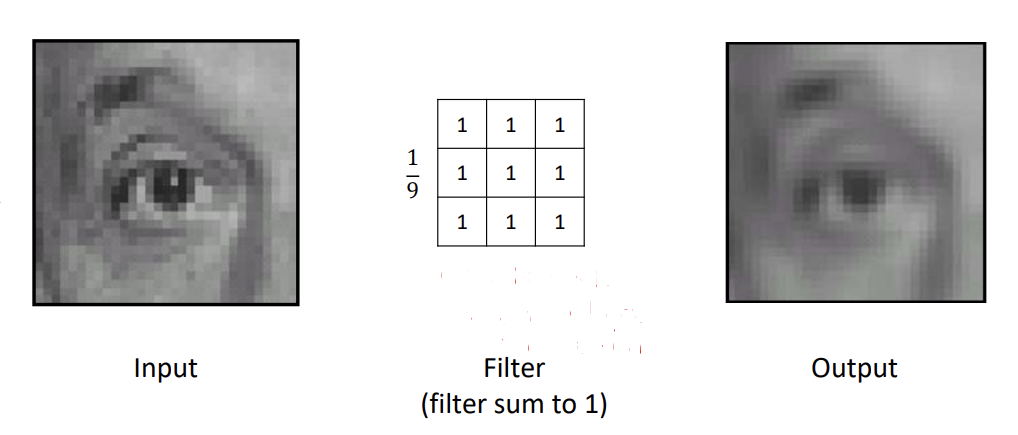
- 평균 필터 내부의 모든 픽셀 값은 동일한 양의 값을 가지며, 그 값들의 합은 항상 1이다.
  - 필터 전체 합이 1보다 큰 경우 : 전체 밝기가 증가
  - 필터 전체 합이 1보다 작은 경우 : 전체 밝기가 감소
- 필터의 size가 커질수록 값에 영향을 주는 픽셀 값들이 많아지므로, 이미지 픽셀이 뭉개지는 현상이 더 두드러진다.

2-2. Gaussian Filter

Gaussian Filter : 중심 픽셀에 가중치를 더 높게 설정하여 필터에 대한 중심 픽셀의 영향력을 높이는 방식이다.
- 가우시안 필터링은 Smoothing 기법 중 하나이지만, 이미지의 특징을 최대한 보존하도록 설계되었다.
- 가우시안 필터링은 특히 노이즈를 제거할 때 자주 사용되는 기법이다.
가우시안 함수
- 가우시안 함수는 정규 분포를 따른다.
- $(x,y)$ 는 필터 중심으로부터의 거리.
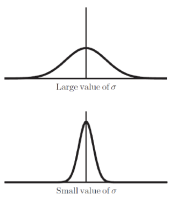
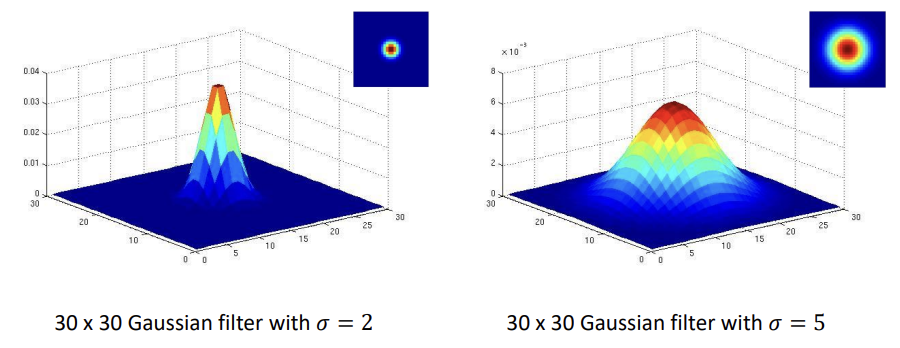
- $\sigma$ 는 가우시안 함수의 표준편차로, 필터가 퍼지는 정도를 결정한다. 즉, 기울기를 나타낸다고 볼 수 있다.
  - $\sigma$ 값이 큰 경우 : 경사가 완만해지고 값들이 전체적으로 고르게 분포한다.
  - $\sigma$ 값이 작은 경우 : 경사가 급해지고 값이 중앙으로 모인다.

$\sigma$ 값이 작아질수록 중심 픽셀의 가중치가 커진다.

2-3. Average Filtering vs Gaussian Filtering

Average Filtering vs Gaussian Filtering
Creation Gaussian Filter : 가우시안 필터의 사이즈와 시그마 값을 적절히 조절해야 "가우시안 필터링"의 효과를 기대할 수 있다. 만약 두 값을 조절하는 것에 실패하면, "가우시안 필터링"과 "평균 필터링"의 결과가 거의 동일하게 나올 수 있다.
- 가우시안 필터의 크기와 표준편차는 서로 영향을 주는 값이다. 따라서 두 값을 적절히 조절해야 한다.
- $size$ 와 $\sigma$ 를 조절하는 원칙은 다음과 같다.
  - 가우시안 필터 요소들의 합은 1이 되어야 한다.
  - 필터 가장자리의 값은 0에 근사해야 한다.
- 일반적으로 가우시안 필터의 크기는 표준 편차(시그마)의 3배에서 5배 사이로 설정한다고 한다.

3. Sharpening

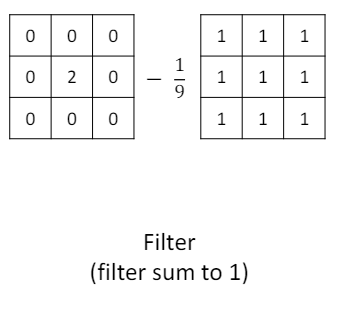
Sharpening : 이미지의 대비 혹은 각 픽셀 간의 값의 차이를 더욱 크게 하여 이미지를 더 선명하게 보이도록 하는 방법.
- 특징을 더욱 부각시키는 효과가 있다.
- 경계가 더욱 선명해진다.
- 마찬가지로 전체적인 밝기가 변하지 않도록 하려면 필터 전체의 합은 1이 되어야한다.

3-1. Unsharp masking

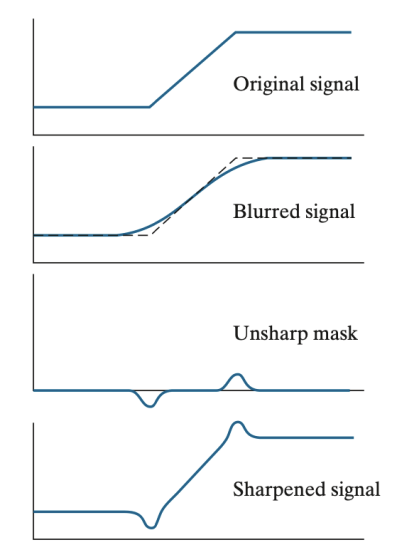
Unsharp masking : 이미지를 더욱 선명하게 만드는 데 사용되는 기법 중 하나로, 이미지의 픽셀의 경계를 더 강조하는 효과가 있다. 이 방식은 다음과 같은 단계로 구성된다.
- 동작 과정
  
  1). 원본 이미지 흐리게(Smoothing) 만들기 : $f(x) \rarr f^{\prime}(x)$
  
  2). 흐린 이미지를 원본 이미지에서 빼기 연산으로 마스크 생성 : $g_{mask}(x) = f(x) - f'(x)$
  
  3). 마스크를 원본에 더하기 : $g(x) = f(x) + kg_{mask}(x)$
  - 위 과정에서 $k$ 값은 sharpening의 정도를 결정하는 값으로, $k$ 값이 커질수록 그 정도가 커진다.
  - 원본 이미지를 흐리게 만들 때, average filter, Gaussian filter 등 어떤 스무딩 기법을 사용해도 상관 없다.

4. Separability

Separability : 2차원 함수 $w(x,y)$ 는 다음과 같이 분리가 가능하다.

$w(x,y) = w_1(x)w_2(y)$
- 이러한 성질은 Convolution Kernel의 효율적인 구현에 매우 유용하게 활용된다.
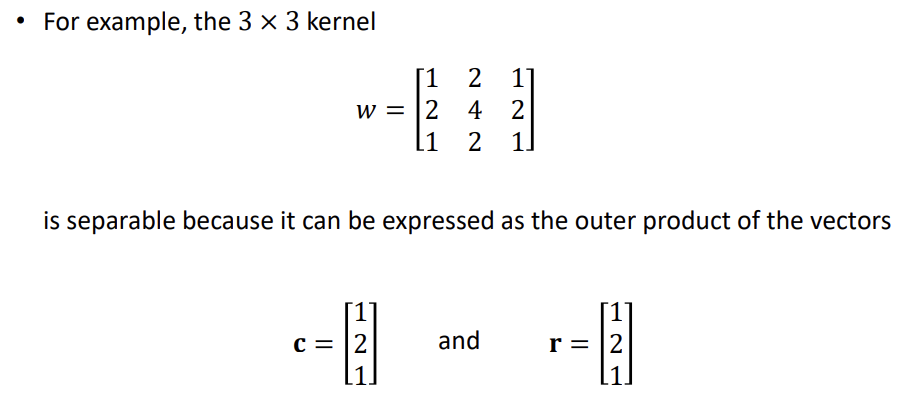
- 예를 들어, $m * n$ 크기의 Convolution Kernel이 분리가 가능하다면, 그것은 두 벡터의 외적으로 표현될 수 있다.
  $c : (m * 1)\,\,size\,\,of\,\,vector \\ r : (n * 1)\,\,size\,\,of\,\,vector \\ w = cr^T$
- 예제
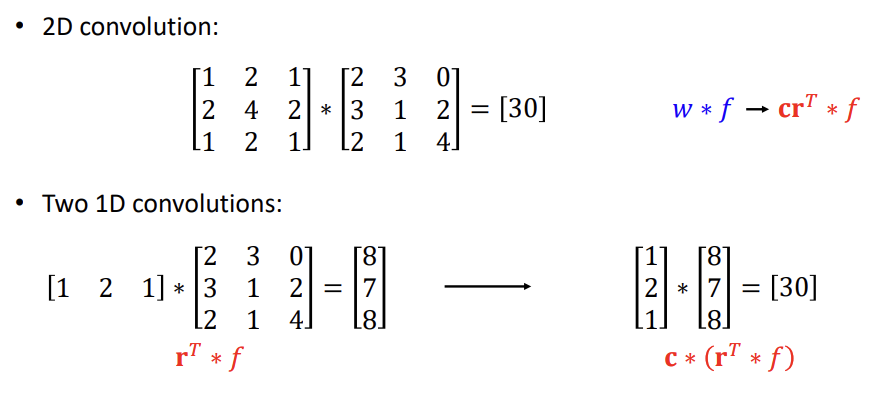
Separability of the Gaussian filter : 2차원 가우시안 함수는 $x$ 와 $y$ 에 대한 두 개의 1차원 함수의 곱으로 표현할 수 있다.
$\begin {aligned} G(x,y) &= G(x)G(y) \\ G(x,y) &= \frac{1}{2\pi\sigma^2}e^{-(\frac{x^2 + y^2}{2\sigma^2})} \\ &= (\frac{1}{\sqrt{2\pi\sigma}}e^{-\frac{x^2}{2\sigma^2}})(\frac{1}{\sqrt{2\pi\sigma}}e^{-\frac{y^2}{2\sigma^2}}) \end {aligned}$
Separability의 유용성 : 연산량 감소 효과를 기대할 수 있다.
- Standard filtering : 필터의 모든 원소가 이미지의 각 픽셀과 곱해져야 한다.
  - 각 픽셀 당 곱셈 횟수 : $K^2$
  - 총 곱셉 횟수 : $K^2 * N^2$
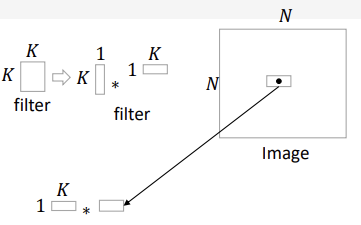
- Separable filtering : 필터를 두 개의 벡터의 외적으로 분리하여 표현할 수 있다면, 가로 방향에 대한 필터링과 세로 방향에 대한 필터링 총 두 번의 필터링을 적용하여도 결과는 동일하다.
  - 각 픽셀 당 곱셈 횟수 : $K * 1 * 2$
  - 총 곱셈 횟수 : $2K * N^2$