알고리즘 스터디에서 dp 대표 문제를 돌아가면서 발표해보자는
의견이 나와서 일주일에 한번씩 돌아가면서 발표중이다.
이번에 내가 맡게된 부분은 배낭채우기 문제인데,
관련 내용을 공부하면서 스터디원들에게 발표하기 위해 정리했던 내용을 공유하고자한다.
배낭 채우기 문제
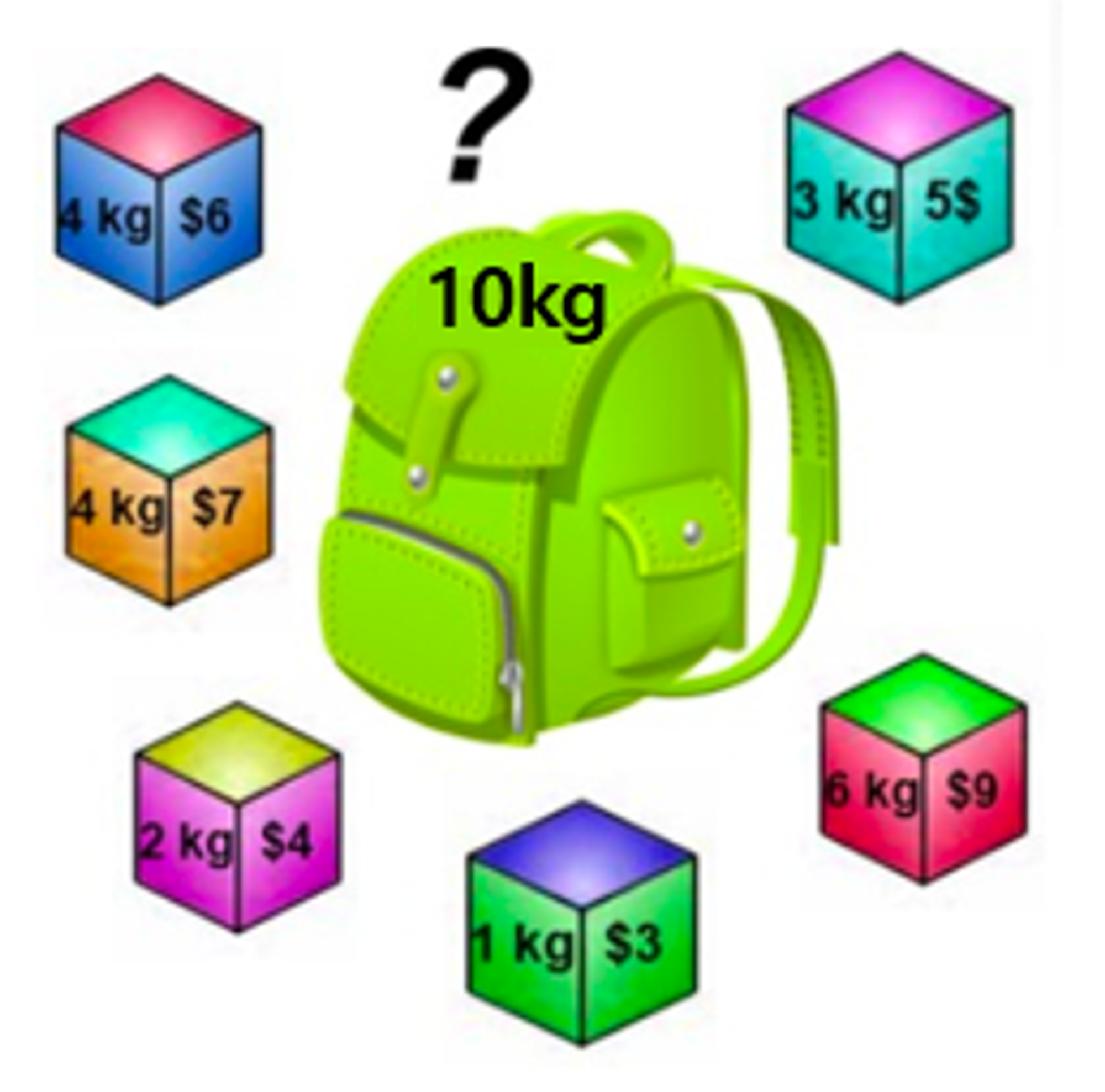
- 일정한 가치와 무게가 정해진 짐들을 배낭에 담을 때, 가치의 합이 최대가 되도록 짐을 고르는 방법을 찾는 문제
종류
- 물건을 쪼갤 수 있는 배낭문제
- 그리디
- 무게 대비 가격이 높은 순으로 넣다가 배낭 용량을 오버하면 물건을 잘라서 넣음
- 물건을 쪼갤 수 없는 배낭문제
- DP
- 그 물건을 포함하거나 안하거나 둘 중 하나만 선택해야 한다.
0/1 배낭문제 풀이
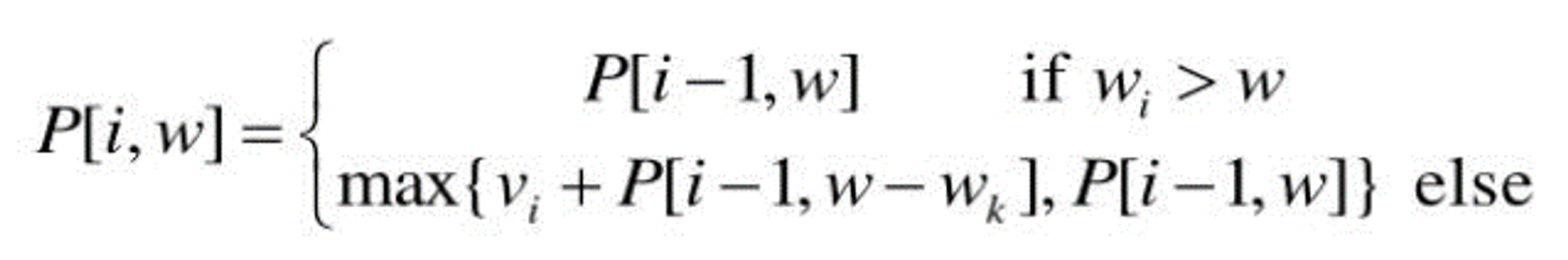
- p[i,w]
- i번 째 까지의 보석이 있고 배낭의 무게한도가 w일 때 최대 이익
- 식의 의미
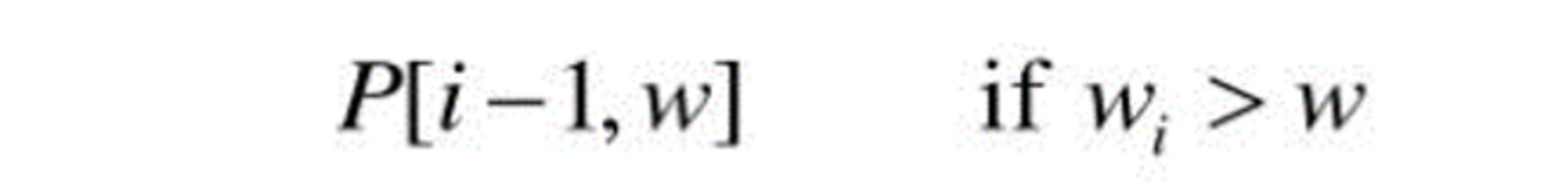
- i번 째 보석이 배낭 무게보다 무거우면(wi>w) 넣을 수 없다. 따라서 i번 째 보석을 뺀 i-1개의 보석들을 가지고 이전에 구했던 최적의 값(p[i-1,w])을 그대로 가져온다.
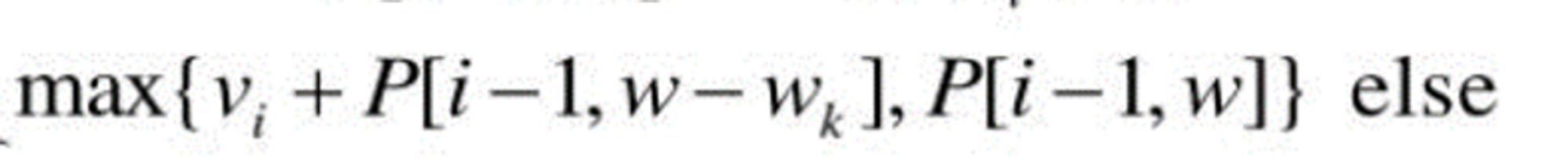
- 이 보석을 넣을 수 있으면 이 보석을 넣지 않았을 때의 최적의 값과 이 보석을 넣었을 때의 최적의 값을 비교해서 최댓값을 넣으면 된다.
- 즉, i번 째 보석을 넣기 위해 i번 째 보석만큼 무게를 비웠을 때의 무게한도에서 i-1개의 보석을 가지고 만들 수 있는 최댓값(p[i-1, w-wk])에 i번 째 보석의 가격을 더한 값(vi)과 i-1개의 보석을 가지고 구한 전단계의 최적값(p[i-1],w) 중 큰 것을 선택한다.
과정
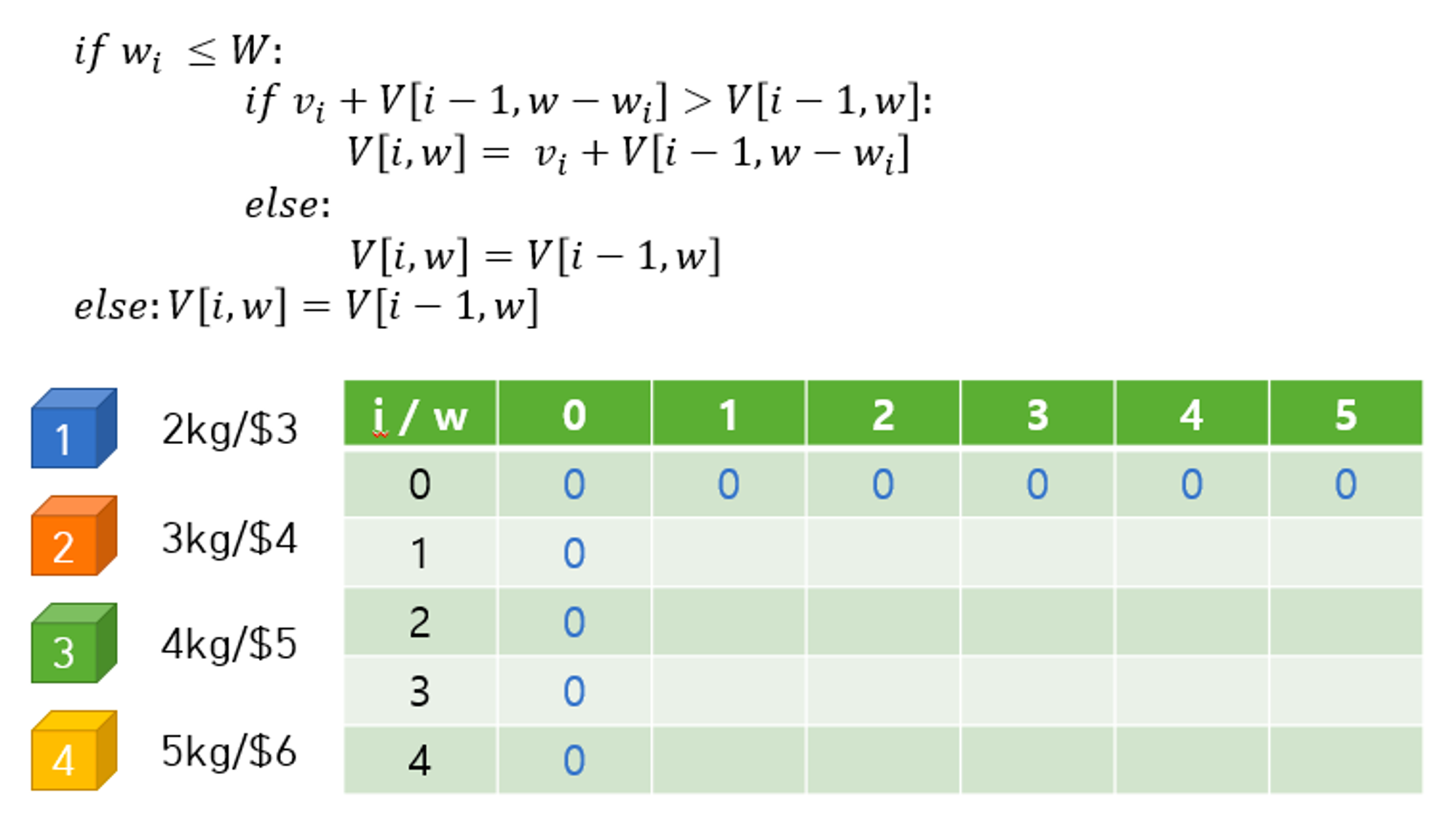
i가 0인 경우는 넣을 보석이 없는 것 ⇒ 모두 0으로 초기화
w가 0인 경우는 배낭의 최대한도가 0인것 ⇒ 모두 0으로 초기화
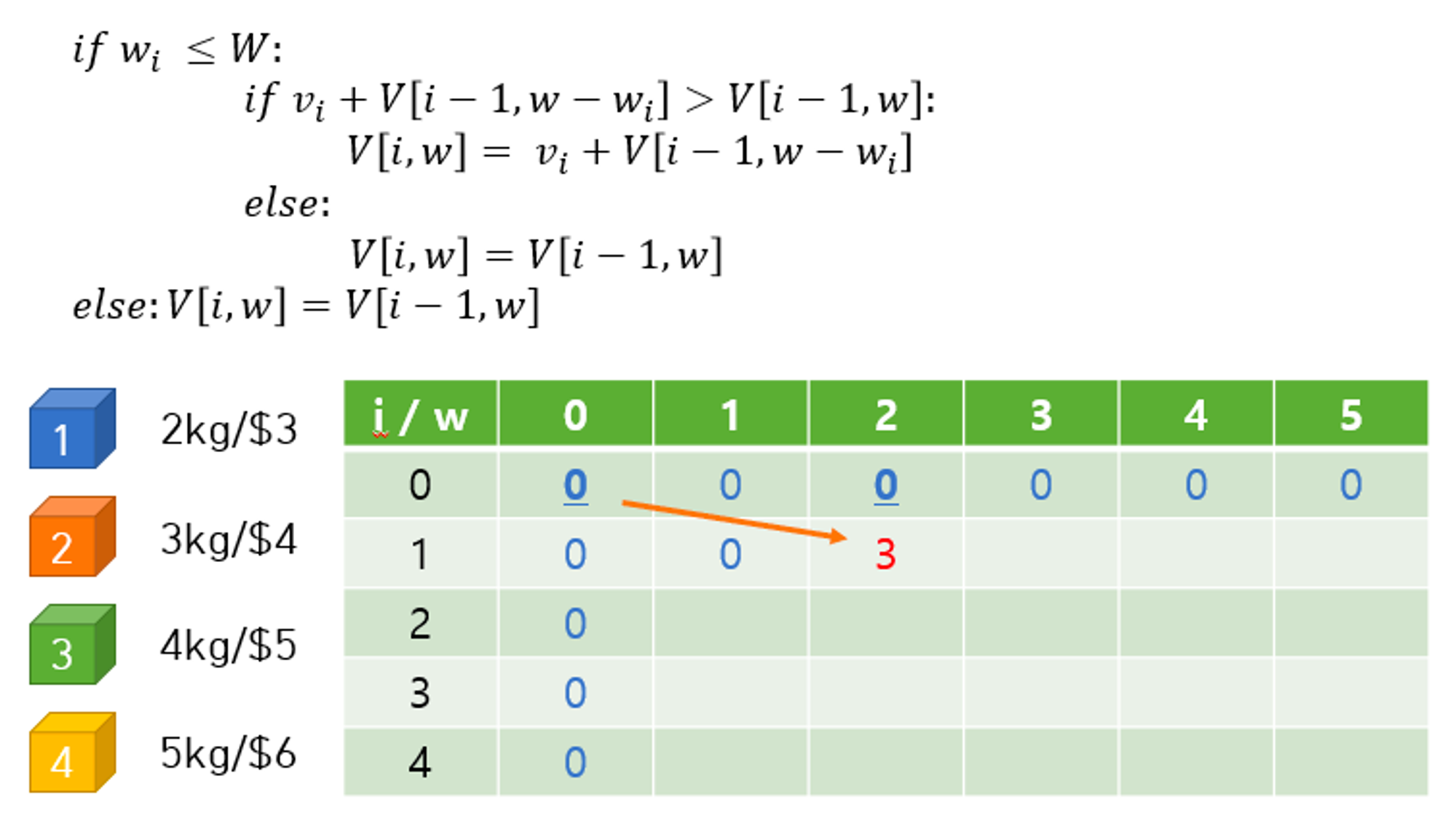
i=1인 경우
w=1짜리 배낭으로는 아무 보석도 넣을 수 없다
→ 0
w=2짜리 배낭에는 현재 보고 있는 보석(1번)을 넣을 수 있다.
→ max(이전값인 p[0,2], 1번 보석 가치 + p[0,0])
→ max(0, 3+ 0) = 3
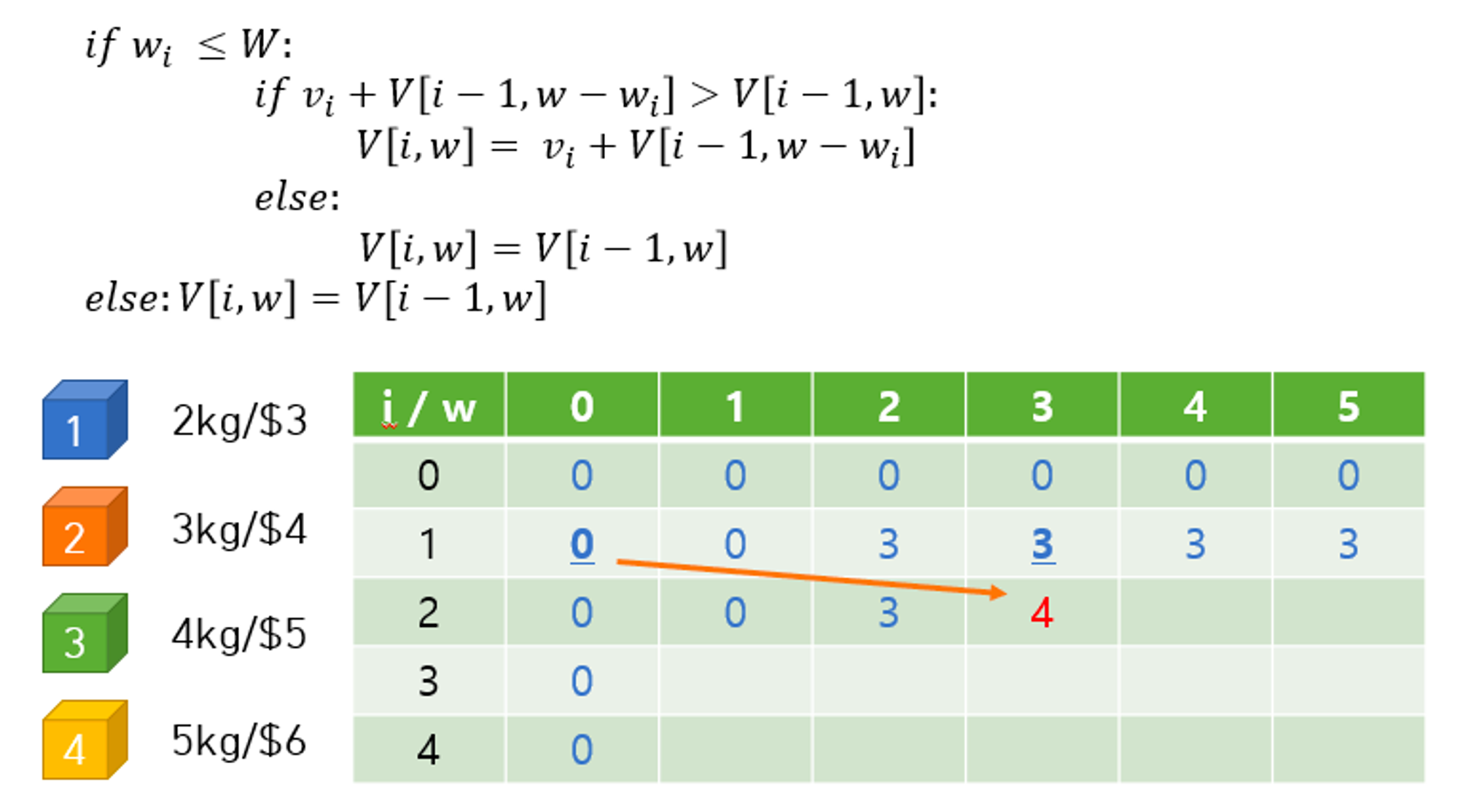
i=2일때,
w=2면 현재 보고 있는 2번 보석을 넣을 수 없으므로 1번 보석만 넣는다(p[1,2])
w=3이 되면 2번 보석을 넣을 수 있다. 따라서 2번 보석을 안넣었을 때(p[1,3] = 3)와 2번 보석을 넣을 만큼 공간을 확보하고 2번 보석을 넣었을 때(2번 보석의 가치 + p[1,0] == 4 + 0)를 비교해 더 가치가 높은 쪽(=4)을 선택한다.
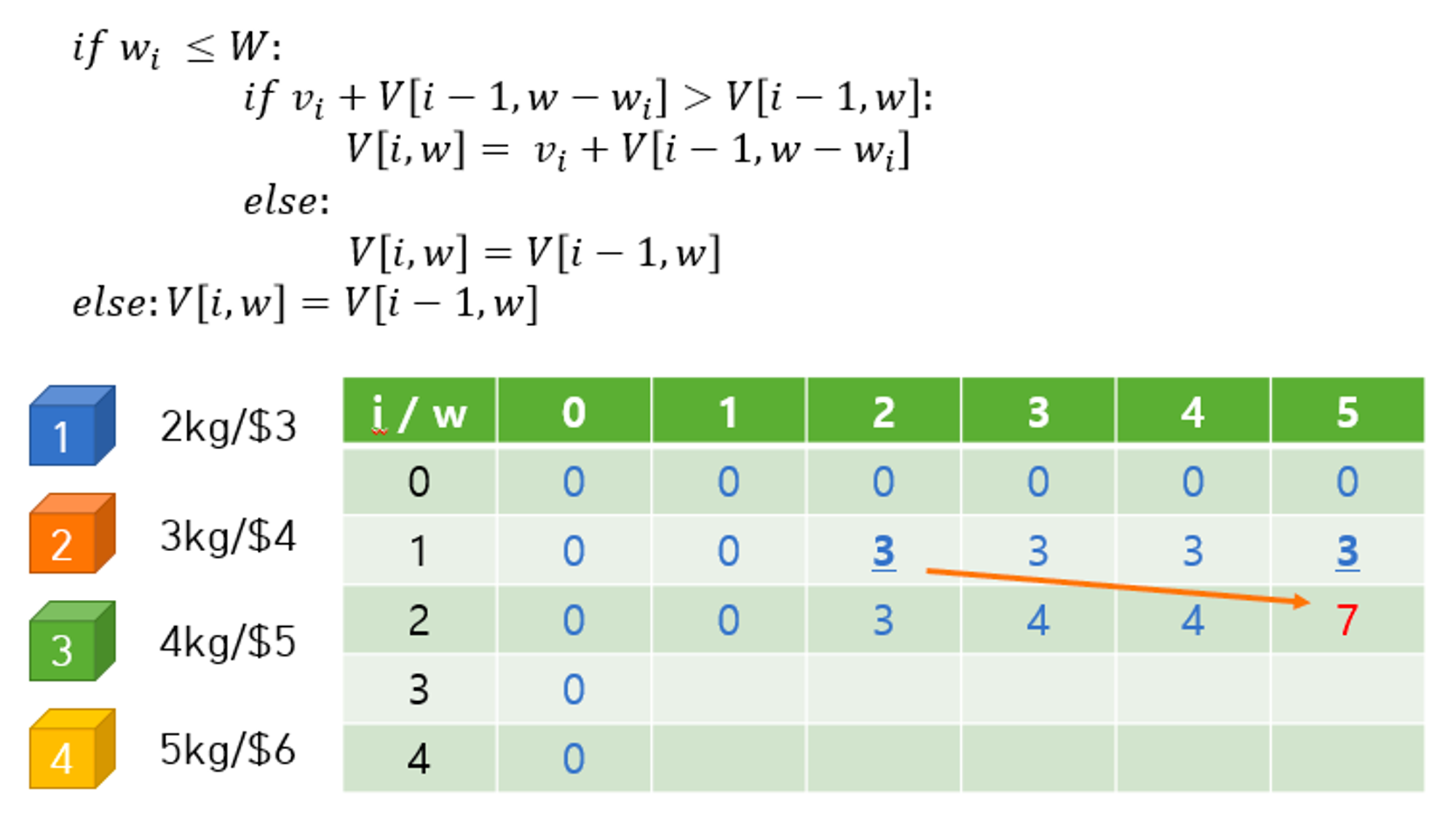
w=5일 경우에는 1번 보석과 2번 보석을 둘 다 넣을 수 있다.
이미 3이 들어있는 (1, 2) 에서 최적값을 가져온다는 것이 1번 보석을 빼지 않고도 2번 보석을 넣을 수 있음을 의미한다. 즉 1번 보석을 넣었던 칸의 최적값 (3) + 2번 보석의 가격 해서 7이 들어간다.
…
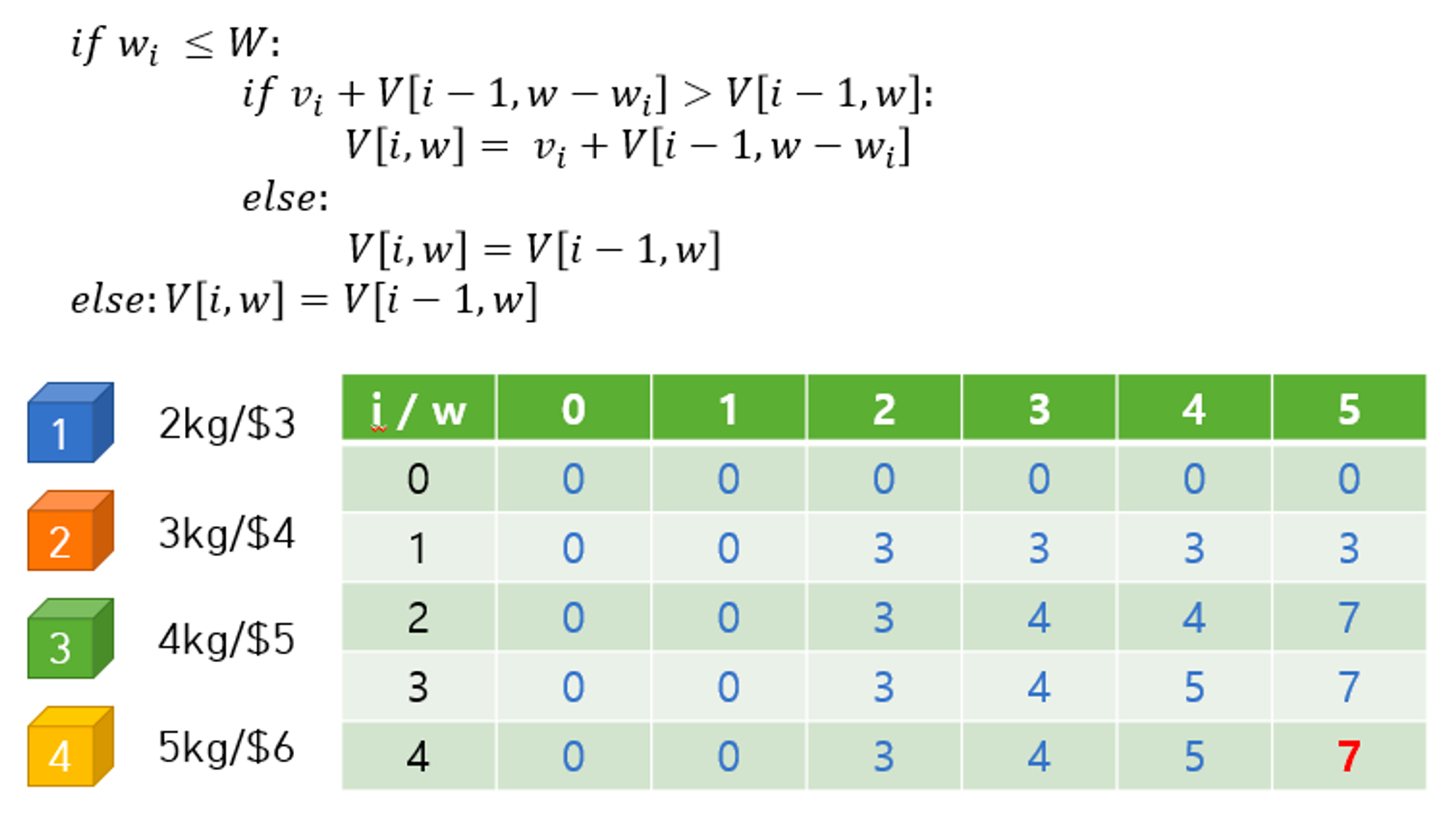
이런 식으로 나머지 칸들도 계산해보면 마지막 칸에는 결국 7이 들어가고, 이 마지막 칸의 값이 최종적인 답 (최적의 총 가격) 이 된다.
코드
def knapsack(W, wt, val, n): # W: 배낭의 무게한도, wt: 각 보석의 무게, val: 각 보석의 가격, n: 보석의 수
K = [[0 for x in range(W+1)] for x in range(n+1)] # DP를 위한 2차원 리스트 초기화
for i in range(n+1):
for w in range(W+1): # 각 칸을 돌면서
if i==0 or w==0: # 0번째 행/열은 0으로 세팅
K[i][w] = 0
elif wt[i-1] <= w: # 점화식을 그대로 프로그램으로
K[i][w] = max(val[i-1]+K[i-1][w-wt[i-1]], K[i-1][w]) # max 함수 사용하여 큰 것 선택
else:
K[i][w] = K[i-1][w]
return K[n][W]예제 - 평범한 배낭
12865번: 평범한 배낭 문제를 예로 풀어보면 더 좋다. 정답 코드는 아래에 남긴다.
def knapsack(W, wt, val, n): # W: 배낭의 무게한도, wt: 각 보석의 무게, val: 각 보석의 가격, n: 보석의 수
K = [[0 for x in range(W+1)] for x in range(n+1)] # DP를 위한 2차원 리스트 초기화
for i in range(n+1):
for w in range(W+1): # 각 칸을 돌면서
if i==0 or w==0: # 0번째 행/열은 0으로 세팅
K[i][w] = 0
elif wt[i-1] <= w: # 점화식을 그대로 프로그램으로
K[i][w] = max(val[i-1]+K[i-1][w-wt[i-1]], K[i-1][w]) # max 함수 사용하여 큰 것 선택
else:
K[i][w] = K[i-1][w]
return K[n][W]