[CS - Algorithm] 최단경로 알고리즘 - 다익스트라 (Dijkstra), 벨만 포드(Bellman-Ford-Moore), 플로이드 워셜 (Floyd-Warshall)

SUN·2022년 11월 4일
다익스트라벨만 포드플로이드 워셜
0

Computer Science

목록 보기
10/11

알고리즘 스터디에서 이번 주는 최단 경로 알고리즘 주제에 대해 문제를 풀게 됐다.
그래서 문제를 풀기 전에 공부한 내용을 공유한다.

최단 경로 알고리즘이란?

그래프에서 간선의 가중치의 합이 최소가 되는 경로를 찾는 문제

최단 경로 문제 종류

  • 단일 출발 (single-source) 최단 경로
    • 하나의 정점에서 출발하여 나머지 모든 정점 까지의 최단 경로를 찾는 문제
  • 단일 도착 (single-destination) 최단 경로
    • 모든 정점에서 출발하여 어떤 하나의 정점까지의 최단 경로를 찾는 문제
    • 그래프 내의 간선들을 뒤집으면 단일 출발 최단거리 문제로 바뀔 수 있다.
  • 단일 쌍(single-pair) 최단 경로
    • 모든 정점 쌍들 사이의 최단 경로를 찾는 문제

주요 알고리즘

  • BFS
    • 가중치가 없거나 모든 가중치가 동일한 그래프에서 최단경로를 구하는 경우 사용
    • 스택 활용
  • 다익스트라 알고리즘 (Dijkstra Algorithm)
    • 음의 간선이 없는 가중 그래프에서의 최단 경로 문제 풀이에 사용
    • 특정 정점에서 갈 수 있는 모든 정점들까지의 최단경로를 구하는 알고리즘
    • 우선순위 큐 활용
      • 다른 방법도 있긴 있는데 보통 우선순위큐를 사용함
      • 정점의 수가 적거나 간선의 수가 매우 많은 경우에는 반복문으로만 푸는 게 나을 수도 있다.
        • 이 경우 O(V^2+E)의 시간복잡도를 가진다.
        • 동작 방식은 다음에 방문할 정점을 별도의 큐에 보관하는 대신
          매번 반복문을 이용해 방문하지 않은 정점 중 dist[]가 가장 작은 값을 찾는다.
    • 그리디
    • gps, 길찾기 서비스
    • O(ElogE) = O(ElogV)
      • 정점마다 인접한 간선 검사 작업의 최악의 시간 복잡도는 O(E)
        • 정점은 한 번만 방문되기 때문에 모든 간선이 한번 씩 검사됨
      • 우선 순위큐에 원소를 넣고 삭제하는 작업의 최악 복잡도는 O(logE)
        • 우선순위 큐에 추가되는 최대 원소수는 E, 우선순위 큐 삽입에 log(E)
      • 그래서 O(ELog(E))가 되지만 O(ElogE)=O(ElogV)라고 볼 수 있다.
        • 대개의 경우 그래프에서 E는 V^2보다 작기 때문
          (사람마다 복잡도 써 놓은 게 다 다르길래 찾아봤더니 이런 거였다..!)
  • 벨만-포드 알고리즘 (Bellman-Ford-Moore Algorithm)
    • 음의 값을 포함한 가중 그래프에서의 최단 경로 문제에 사용
    • 동적 계획법
    • 최악 O(V^3), 보통 O(VE)
      • V마다 모든 E를 탐색하기 때문에 O(VE)
      • 모든 노드에 간선이 연결되어 있다면 라면 E는 V^2에 근사해지므로 O(v^3)
  • 플로이드-워셜 알고리즘 (Floyd-Warshall Algorithm)
    • 모든 정점 쌍들 사이의 최단경로를 구하는 문제에 사용
    • 동적 계획법
    • 음의 가중치 처리 가능
    • O(V^3)
      • 현재 노드를 거쳐가는 모든 경로를 고려하는 O(n^2) 연산을 각각의 경유 노드마다 반복해야 하므로

이제 각 알고리즘에 대해 좀 더 자세히 알아보겠다.

다익스트라(Dijkstra) 알고리즘

특정한 노드에서 출발하여 다른 노드로 가는 각각의 최단 경로를 구해주는 알고리즘이다.
음의 간선(0보다 작은 값을 가지는 간선)이 없을 때 정상적으로 동작한다.
매번 방문하지 않은 노드 중에서 최단 거리가 가장 짧은 노드를 선택하여 한 단계씩 최단 거리를 구해나간다.

기본 알고리즘

  1. 출발 노드와 도착 노드를 설정한다.
  2. 최단 거리 테이블을 초기화한다.
  3. 현재 위치한 노드의 인접 노드 중 방문하지 않은 노드를 구별하고,
    방문하지 않은 노드 중 거리가 가장 짧은 노드를 선택하고 그 노드를 방문 처리한다.
  4. 해당 노드를 거쳐 다른 노드로 넘어가는 경로의 가중치를 계산해
    원래보다 더 작으면 최단 거리 테이블을 업데이트한다.
  5. 3~4의 과정을 반복한다.

동작 과정

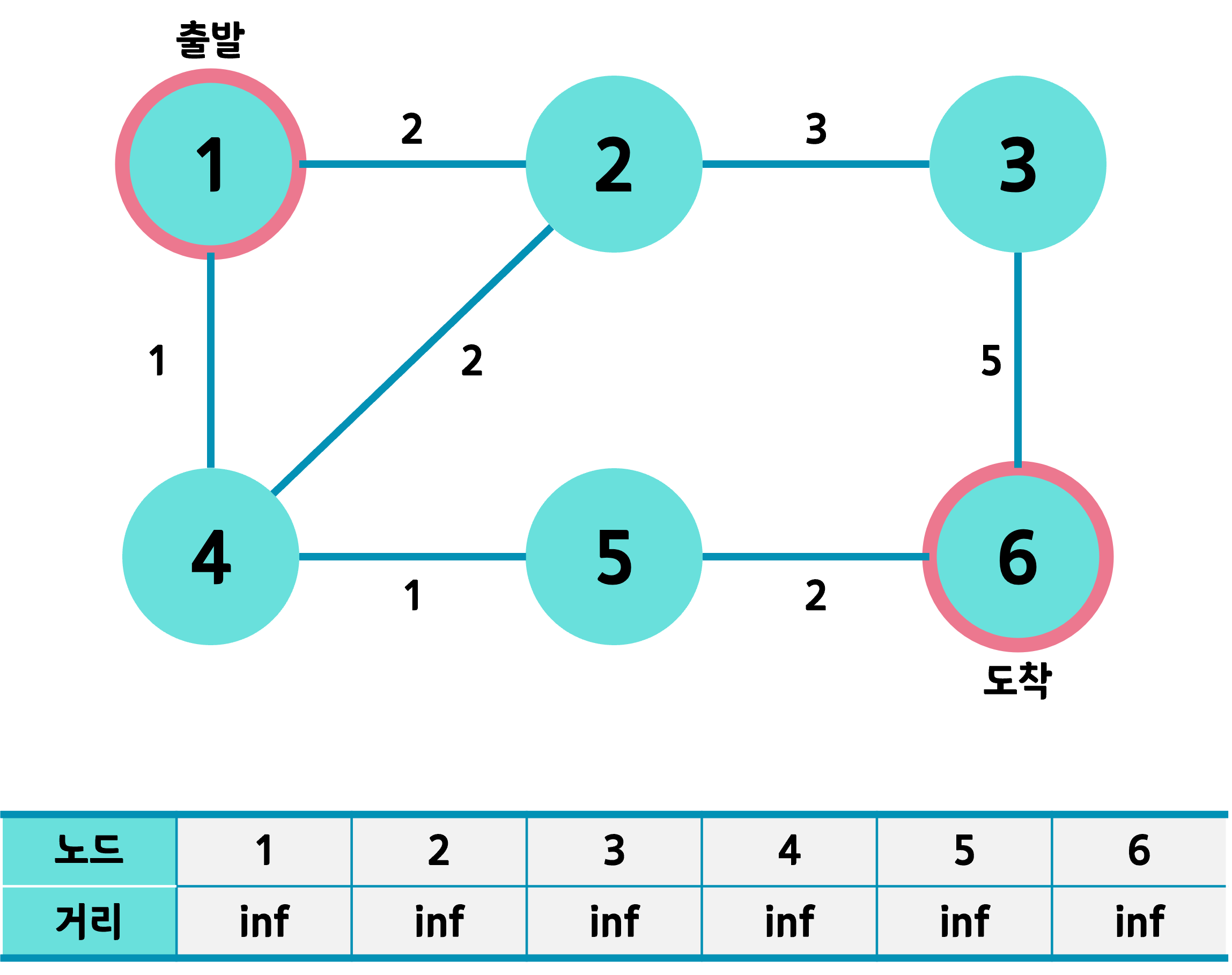
출발 노드는 1번, 도착 노드는 6번이라 하고 (1번 과정)
거리 테이블을 전부 무한대로 초기화한다. (2번 과정)

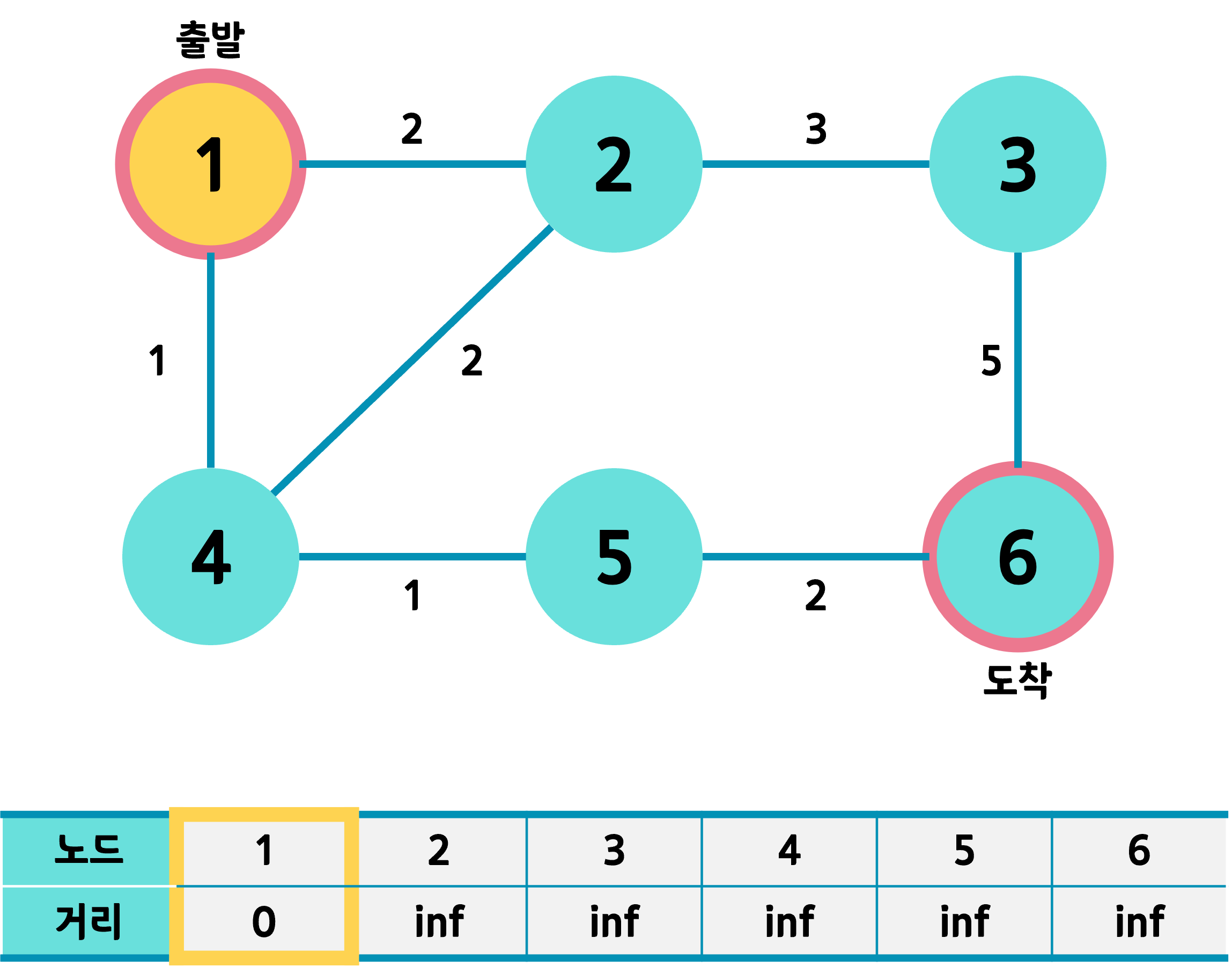
출발 노드를 먼저 선택해서 자기자신이므로 거리를 0으로 변경한다.
그리고 출발 노드와 연결된 방문하지 않은 노드들을 힙에 집어넣는다.

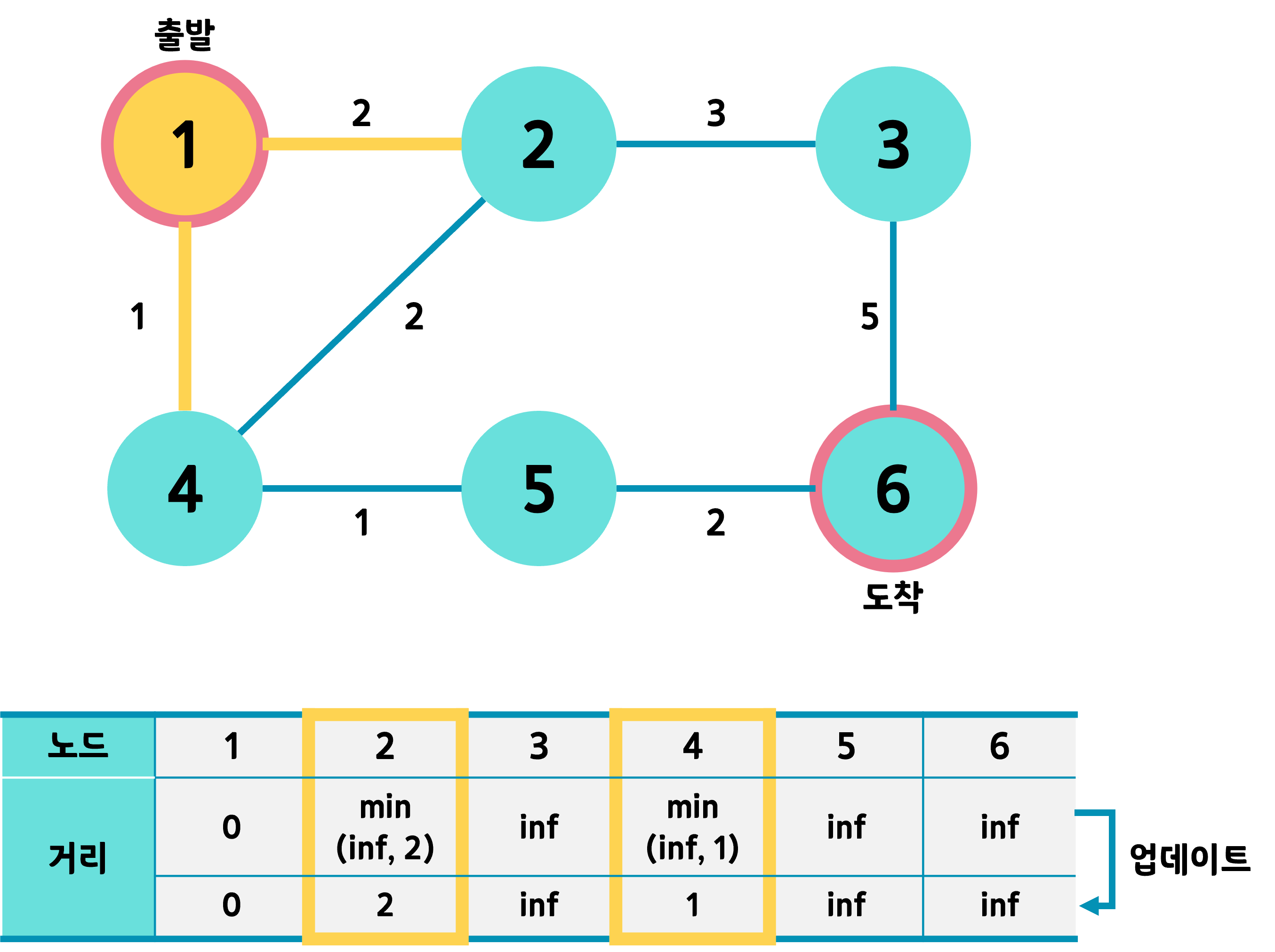
1번 노드와 연결된 인접 노드는 2, 4이다.
1번 노드를 거쳐 각 노드까지 가는 거리를 기존과 비교해 최솟값으로 업데이트 한다.

또한 인접 노드까지의 거리를 모두 업데이트한 1번 노드는 방문 표시를 한다.
그리고 현재 노드의 인접 노드 중 방문하지 않는 노드 중 가장 거리값이 작은 번호를 다음 노드로 택한다.
여기선 4번 노드가 된다.

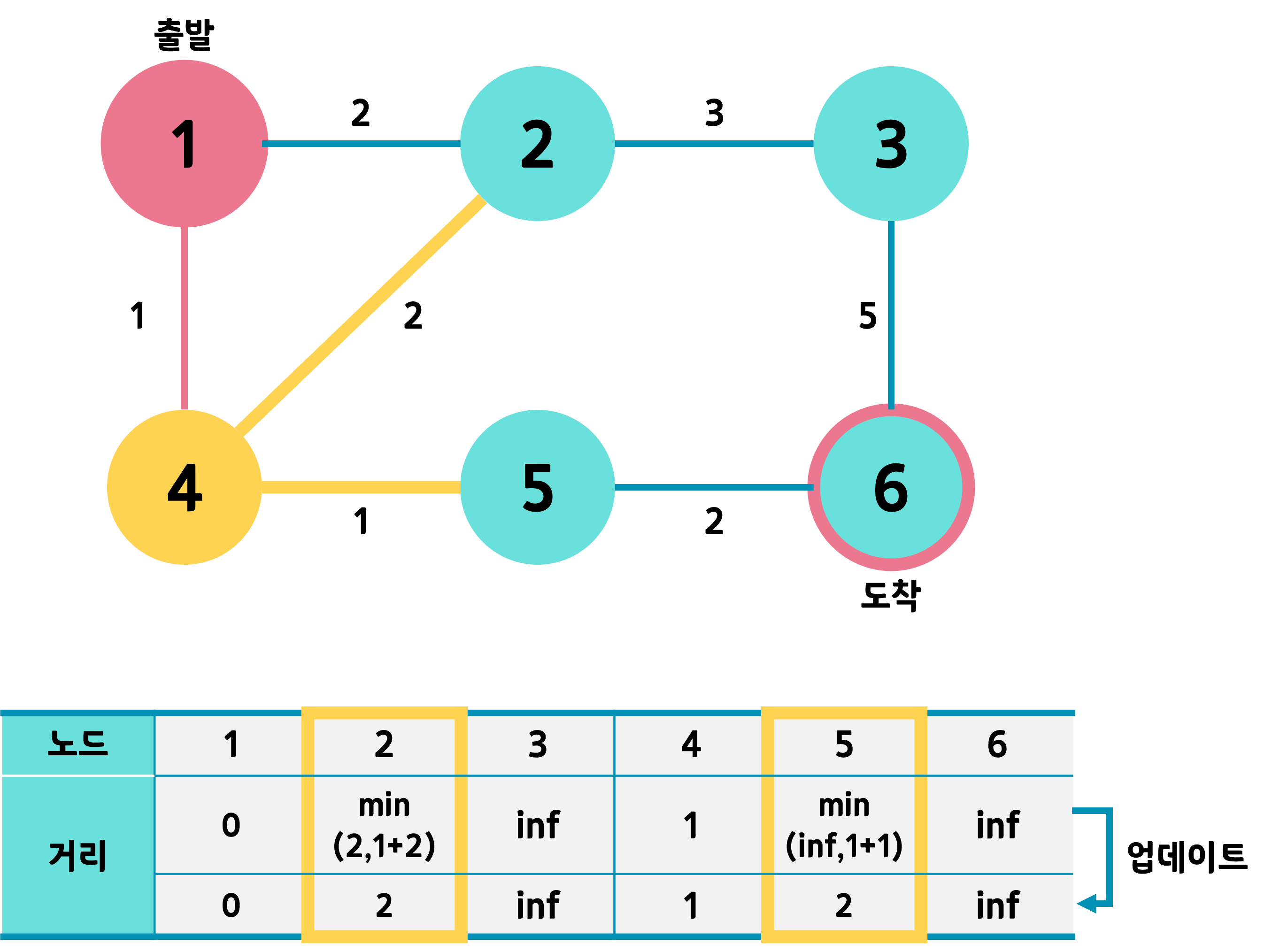
4번 노드에서도 같은 작업을 수행한다.
예를 들어서 5번 노드 같은 경우에는 기존 값 inf와 4번을 거쳐서 5번까지 가는 거리 2 중 최솟값인 2를 저장한다.
2번 노드같은 경우네는 기존 값인 2와 4번을 거쳐 가는 3 중에 2가 최솟값이니까 그대로 둔다.
그리고 방문하지 않은 노드 중에 거리값이 가장 작은 2,5 중에 하나를 선택한다.

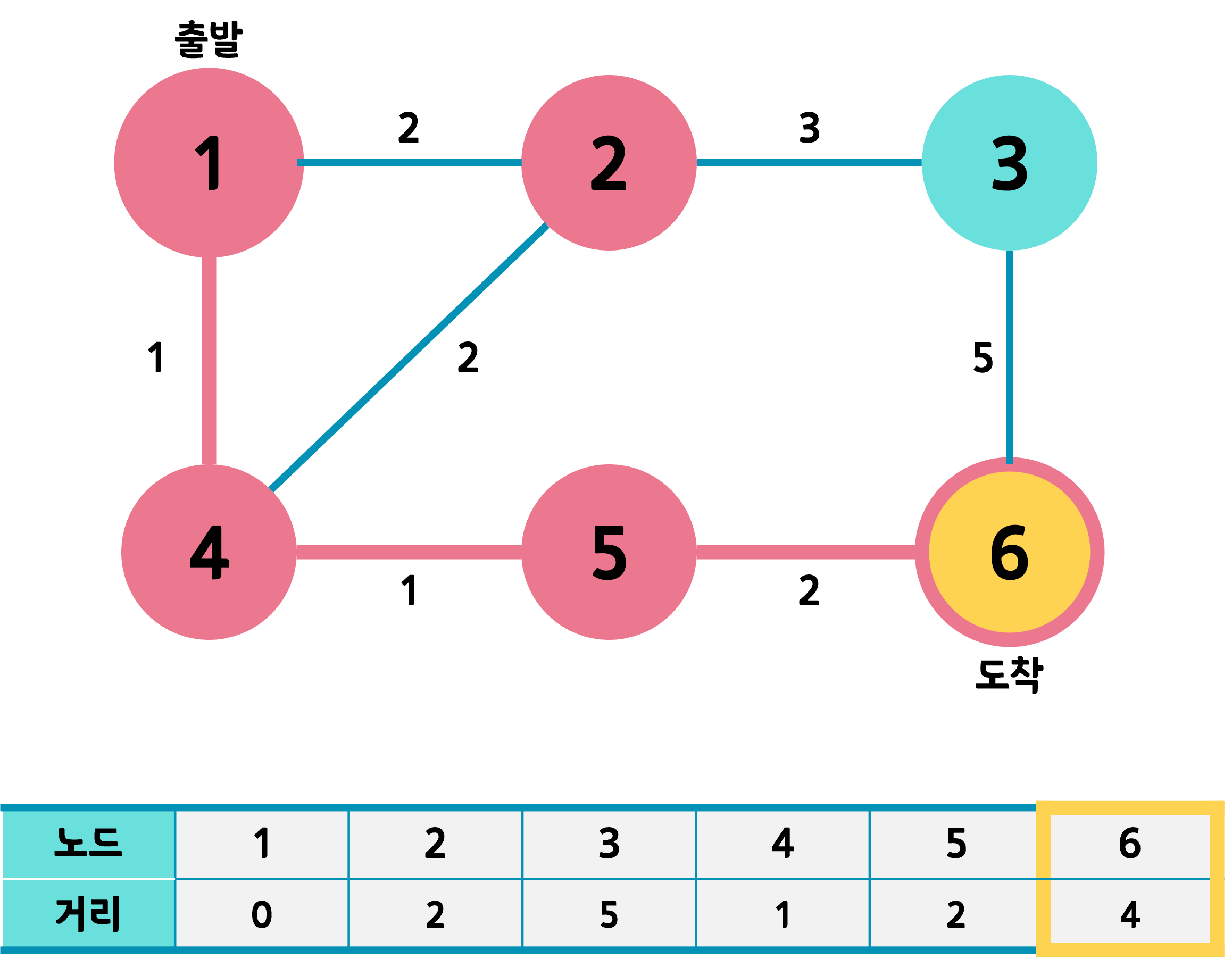
이걸 도착 노드에 도착할 때 까지 반복하면 이렇게 된다.

코드

import heapq  # 우선순위 큐 구현을 위함

def dijkstra(graph, start):
  distances = {node: float('inf') for node in graph}  # start로 부터의 거리 값을 저장하기 위함
  distances[start] = 0  # 시작 값은 0이어야 함
  queue = []
  heapq.heappush(queue, [distances[start], start])  # 시작 노드부터 탐색 시작 하기 위함.

  while queue:  # queue에 남아 있는 노드가 없으면 끝
    current_distance, current_destination = heapq.heappop(queue)  # 탐색 할 노드, 거리를 가져옴.

    if distances[current_destination] < current_distance:  # 기존에 있는 거리보다 길다면, 볼 필요도 없음
      continue
    
    for new_destination, new_distance in graph[current_destination].items():
      distance = current_distance + new_distance  # 해당 노드를 거쳐 갈 때 거리
      if distance < distances[new_destination]:  # 알고 있는 거리 보다 작으면 갱신
        distances[new_destination] = distance
        heapq.heappush(queue, [distance, new_destination])  # 다음 인접 거리를 계산 하기 위해 큐에 삽입
    
  return distances

bfs와 유사한 모습을 보인다.

벨만-포드 알고리즘

음의 가중치를 가진 간선이 있는 그래프에서의 최단 경로 문제에 사용한다.
매 단계마다 모든 간선을 전부 확인하면서 모든 노드간의 최단 거리를 구해나간다.

참고로 다익스트라와 차이점은 매 반복마다 모든 간선을 확인한다는 것이다.
다익스트라는 방문하지 않은 노드 중에서 최단 거리가 가장 가까운 노드만을 방문한다.

알고리즘

  1. 출발 노드를 설정한다.
  2. 최단 거리 테이블을 초기화한다.
  3. 다음의 과정을 (V - 1)번 반복한다.
    1. 모든 간선 E개를 하나씩 확인한다.
    2. 각 간선을 거쳐 다른 노드로 가는 비용을 계산하여 최단 거리 테이블을 갱신한다.
  4. 만약 음수 간선 순환이 발생하는지 체크하고 싶다면 3번 과정을 한 번 더 수행한다.
    --> 이때 최단 거리 테이블이 갱신된다면 음수 간선 순환이 존재하는 것이다.

왜 V-1번 반복할까? 궁금해서 찾아봤다.
V개의 정점과 E개의 간선이 있는 가중 그래프에서
정점 A에서 정점 B까지의 최단 거리는 최대 V-1개의 정점을 지나기 때문이라고 한다.
V-1개 이상의 정점을 방문하는 것은 결국 중복 방문을 하는 것이기 때문에 최단 경로가 성립될 수 없다.

왜 3번 과정을 한번 더 수행하면 음수 간선 순환 여부를 알 수 있을까? 궁금해서 찾아봤다.

한 정점에서 다른 정점까지 최단경로는 아무리 많아도 V-1개의 간선밖에 지날 수 없다.
하지만 음의 사이클이 존재한다면 지나는 간선이 V-1개를 넘어도 더 짧은 경로를 찾을 수 있을 것이다.
따라서 최소 V번의 Iteration을 하게 된다면 음의 사이클 존재 여부도 파악할 수 있다.

그리고 이런 음의 사이클을 발견했다면 최단경로가 존재하지 않는다고 결론짓는다.

동작 방식

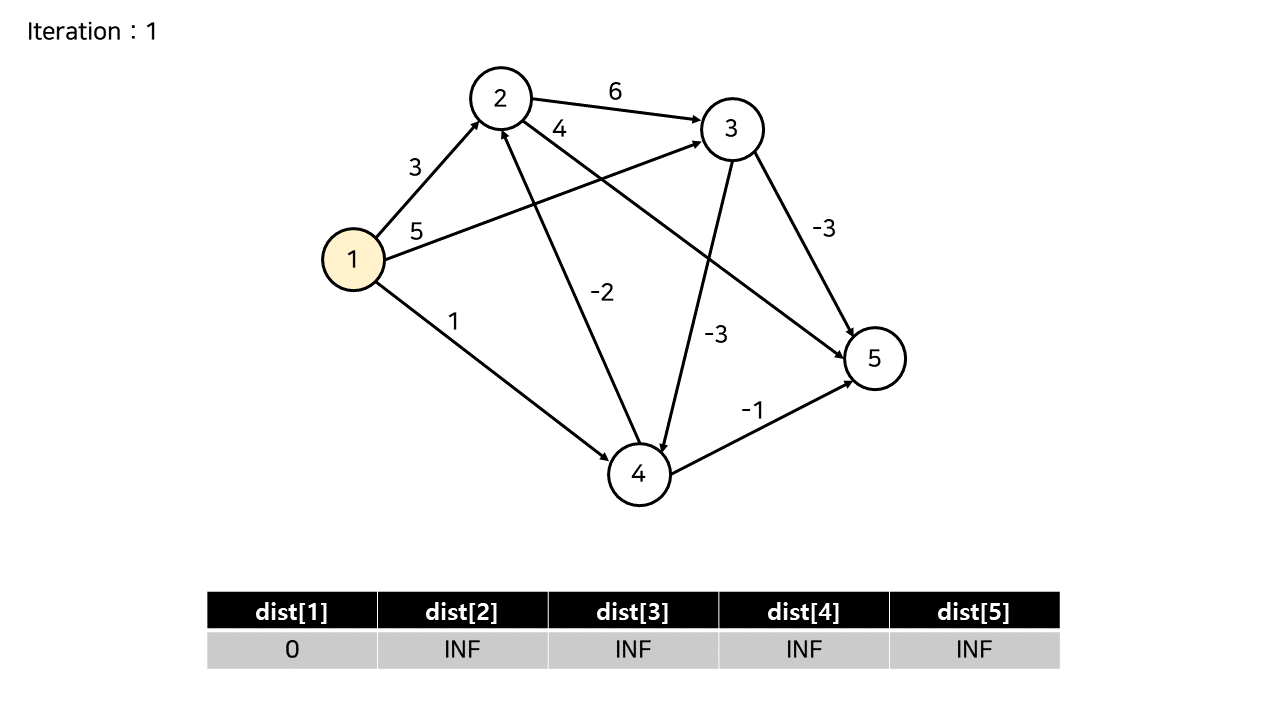
시작 정점이 1이고 나머지 노드들 간에 최단 거리를 구한다고 해보자.
1번 정점에서 다른 정점으로 가는 비용은 1차원 배열로 표현한다.
초기에는 자기 자신은 0, 나머지는 inf로 초기화 한다.
처음 iteration은 출발 노드인 1번 노드에 대해 시작한다.

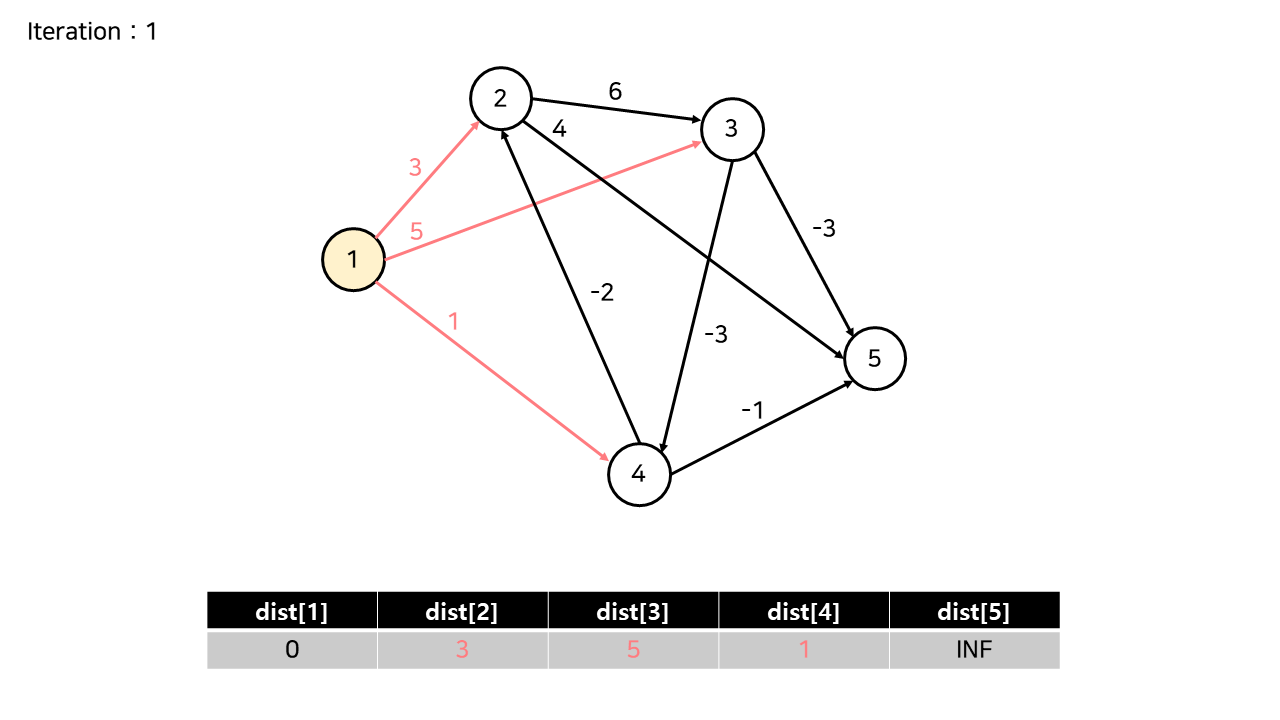
1번 노드에서 나가는 3개의 간선에 의해 dist[2], dist[3], dist[4]가 갱신된다.
예를 들어서 dist[2]같은 경우는 원래 있던 최솟값 inf와 3(1->2 가중치)중에 최소인 3으로 변경된다.

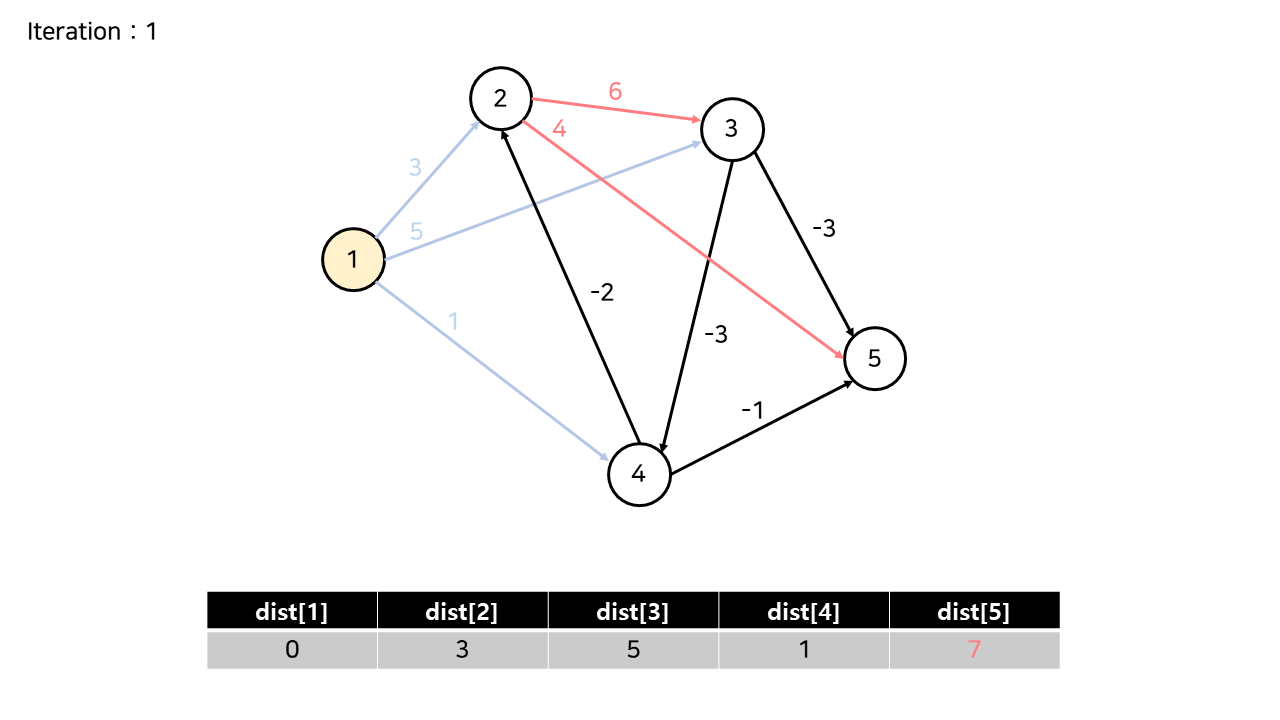
2번 노드에서 나가는 간선에 의해 dist[5]가 7로 갱신되었고, dist[3]은 유지된다.
예를 들어서 dist[3]같은 경우에는 원래 있던 최솟값 5와,
2를 거쳐서 3으로 가는 값 1->2 최솟값+6(2->3 가중치) 중에 원래가 최소이므로 갱신을 하지 않는다.

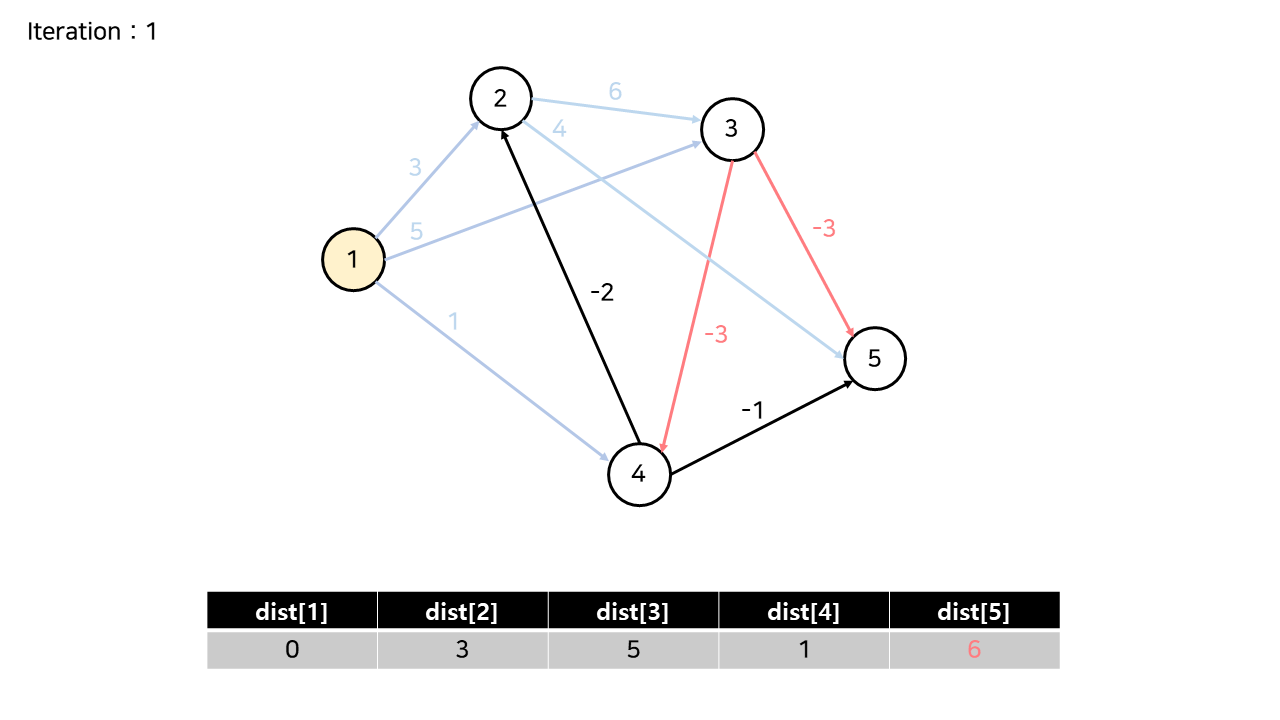
3번 노드에서 나가는 간선들에 의해 dist[5]가 6으로 갱신되고 dist[4]는 유지된다.
예를 들어서 dist[5]같은 경우에는 원래 최솟값 7과
1->2->3의 최솟값 9와 3->5 가중치 -3 을 더한 6을 비교했을 때 6이 최소이므로 업데이트 한다.

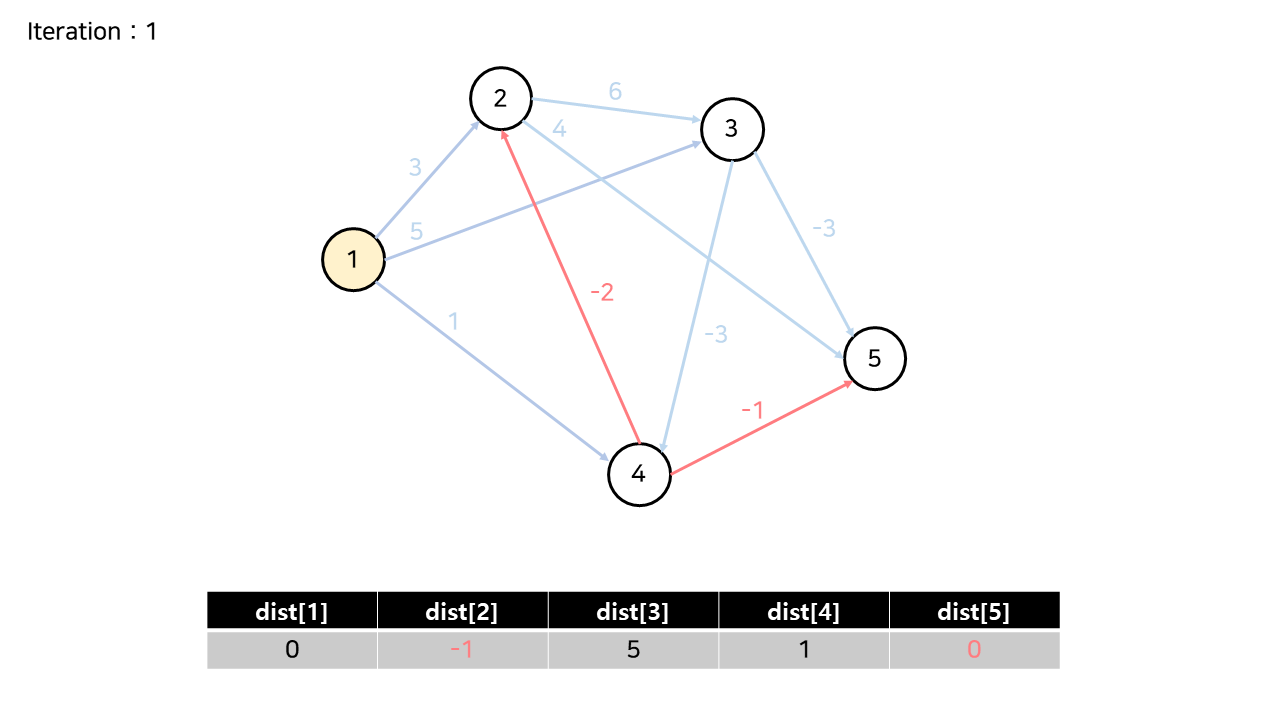
4번 노드에서 나가는 간선들에 의해 dist[2]와 dist[5]가 갱신된다.

길었다.. 하지만 여기까지가 하나의 iteration이다.
이걸 다른 정점 모두에 대해 반복해야 한다.

이렇게 다 끝나고 나서 음수 간선 사이클이 발생했는 지 확인하고
존재하면 최단 경로가 존재 하지 않는다고 결론 내리고
아니라면 찾은 최단 경로를 토대로 결론을 내면 된다.

코드

import sys

input = sys.stdin.readline
INF = int(1e9)

# 노드의 개수, 간선의 개수를 입력
v, e = map(int, input().split())
# 모든 간선에 대한 정보를 담는 리스트 만들기
edges = []
# 최단 거리 테이블을 모두 무한으로 초기화
distance = [INF] * (v + 1)

# 모든 간선의 정보 입력
for _ in range(e):
    a, b, c = map(int, input().split())
    # a번 노드에서 b번 노드로 가는 비용이 c라는 의미 (a -> b 의 비용이 c)
    edges.append((a, b, c))


def bellman_ford(start):
    # 시작 노드에 대해서 초기화
    distance[start] = 0
    # 전체 v - 1번의 라운드(round)를 반복
    for i in range(v):
        # 매 반복마다 '모든 간선'을 확인한다.
        for j in range(e):
            cur_node = edges[j][0]
            next_node = edges[j][1]
            edge_cost = edges[j][2]
            # 현재 간선을 거쳐서 다른 노드로 이동하는 거리가 더 짧은 경우
            if distance[cur_node] != INF and distance[next_node] > distance[cur_node] + edge_cost:
                distance[next_node] = distance[cur_node] + edge_cost
                # v번째 라운드에서도 값이 갱신된다면 음수 순환이 존재
                if i == v - 1:
                    return True

    return False


# 벨만 포드 알고리즘 수행
negative_cycle = bellman_ford(1)

# 음수 순환이 존재하면 -1 출력
if negative_cycle:
    print("-1")
else:
    # 1번 노드를 제외한 다른 모든 노드로 가기 위한 최단 거리를 출력
    for i in range(2, v + 1):
        # 도달할 수 없는 경우, -1 출력
        if distance[i] == INF:
            print("-1")
        # 도달할 수 있으면 거리 출력
        else:
            print(distance[i])

플로이드 워셜

모든 지점에서 다른 모든 지점까지의 최단 경로를 모두 구해야 할 때 사용할 수 있는 알고리즘이다.
2차원 리스트에 ‘최단 거리' 정보를 저장한다.
i 로 부터 j 까지의 거리를 구하는데 k 라는 지점을 거쳐서 지나가는 것이 빠른지 아닌지를 판별한다.

다익스트라의 경우 단계마다 최단 거리를 가지는 노드를 하나씩 반복적으로 선택한다.
이후 해당 노드를 거쳐가는 경로를 확인하며 최단 거리 테이블을 갱신하는 방식으로 동작한다.

플로이드 워셜 알고리즘 또한 단계마다 '거쳐 가는 노드'를 기준으로 알고리즘을 수행한다.
하지만 매 단계마다 방문하지 않은 노드 중에서 최단 거리를 갖는 노드를 찾을 필요가 없다.

동작 방식

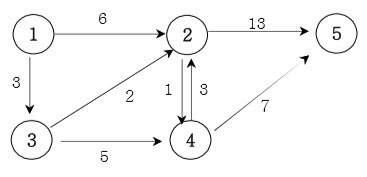
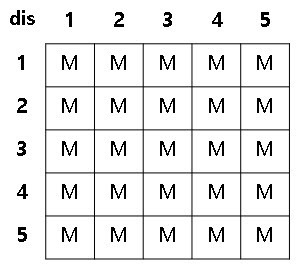
위와 같은 그래프에서 모든 정점 사이의 최단 거리를 구해보자.
우선 큰 값으로 dist 배열을 초기화 해 준다.


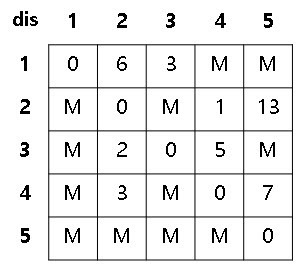
자기자신으로 가는 비용은 0이니까 0으로 변경해준다.
그리고 입력으로 주어진 인접행렬 정보를 dist에 저장한다.

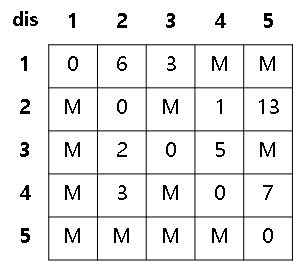
이제 i부터 j까지 이동하는 최소 비용을 구할 건데,
i~j사이에 1~n까지의 정점을 모두 넣어보면서 최소 비용을 구하면 된다.

k=1일 때,
1을 i~j까지의 거리에 모두 넣어보고 기존보다 작으면 업데이트한다.
min(dist[i][j], dist[i][k]+dist[k][j]) 이렇게 계산 하면 된다.

k = 1 && i == 1 일 때,
1->1->1은 (1->1)과 같고,
1->1->2은 (1->2)와 같고,
1->1->3은 (1->3)과 같고 ....

그래서 업데이트 되지 않는다.

k = 1 && i = 2 일 때,

2->1->1 = 갈 수 없음, 원래 값인 M 그대로 둔다.
2->1->2 = 2에서 1로 갈 수 없다. 결과는 M+6이 되어 원래 값 0 그대로 둔다.
2->1->3 = 마찬가지로 2에서 1로 갈 수 없다. 결과는 M+3이 되어 원래값 M 그대로 둔다.
2->1->4 = 2에서 1을 갈 수 없고 1에서 4로도 갈 수 없다. 결과는 M+M이 되어 원래값 1 그대로 둔다.

...

이걸 i를 늘려가면서 끝까지 계속 반복하면 된다.

그러면 결과는 원래와 그대로 나온다.
i부터 j까지 1을 거쳐서 갔을 때, 더 적은 비용으로 가는 경우가 없다는 뜻이다.

그리고 이제 k=2,3...5까지 위의 과정을 반복하면 된다.

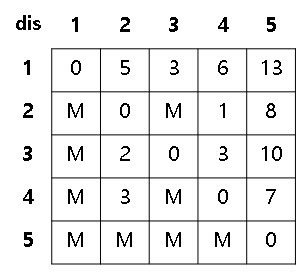
그러면 이런 결과가 나온다!

코드

INF = int(1e9) # 무한을 의미하는 값으로 10억을 설정

# 노드의 개수 및 간선의 개수를 입력받기
n = int(input())
m = int(input())
# 2차원 리스트(그래프 표현)를 만들고, 모든 값을 무한으로 초기화
graph = [[INF] * (n + 1) for _ in range(n + 1)]

# 자기 자신에서 자기 자신으로 가는 비용은 0으로 초기화
for a in range(1, n + 1):
    for b in range(1, n + 1):
        if a == b:
            graph[a][b] = 0

# 각 간선에 대한 정보를 입력 받아, 그 값으로 초기화
for _ in range(m):
    # A에서 B로 가는 비용은 C라고 설정
    a, b, c = map(int, input().split())
    graph[a][b] = c

# 점화식에 따라 플로이드 워셜 알고리즘을 수행
for k in range(1, n + 1):
    for a in range(1, n + 1):
        for b in range(1, n + 1):
            graph[a][b] = min(graph[a][b], graph[a][k] + graph[k][b])

# 수행된 결과를 출력
for a in range(1, n + 1):
    for b in range(1, n + 1):
        # 도달할 수 없는 경우, 무한(INFINITY)이라고 출력
        if graph[a][b] == 1e9:
            print("INFINITY", end=" ")
        # 도달할 수 있는 경우 거리를 출력
        else:
            print(graph[a][b], end=" ")
    print()

참고

https://cs-vegemeal.tistory.com/56
https://velog.io/@717lumos/%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98-%EB%8B%A4%EC%9D%B5%EC%8A%A4%ED%8A%B8%EB%9D%BCDijkstra-%EC%95%8C%EA%B3%A0%EB%A6%AC%EC%A6%98
https://justkode.kr/algorithm/python-dijkstra
https://4legs-study.tistory.com/26
https://data-make.tistory.com/394

profile
SUN
개발자
이전 포스트

[CS - 자료구조] 해시 테이블 (Hash Table) 개념 정리

다음 포스트

[CS - 알고리즘] Knapsack

0개의 댓글