[백준 BOJ] 1018 : 체스판 다시 칠하기 - python

SUN·2022년 10월 5일

python 백준 브루트포스 알고리즘 파이썬

algorithm

목록 보기

21/30

오늘 풀 문제는 체스판 다시 칠하기이다.

문제

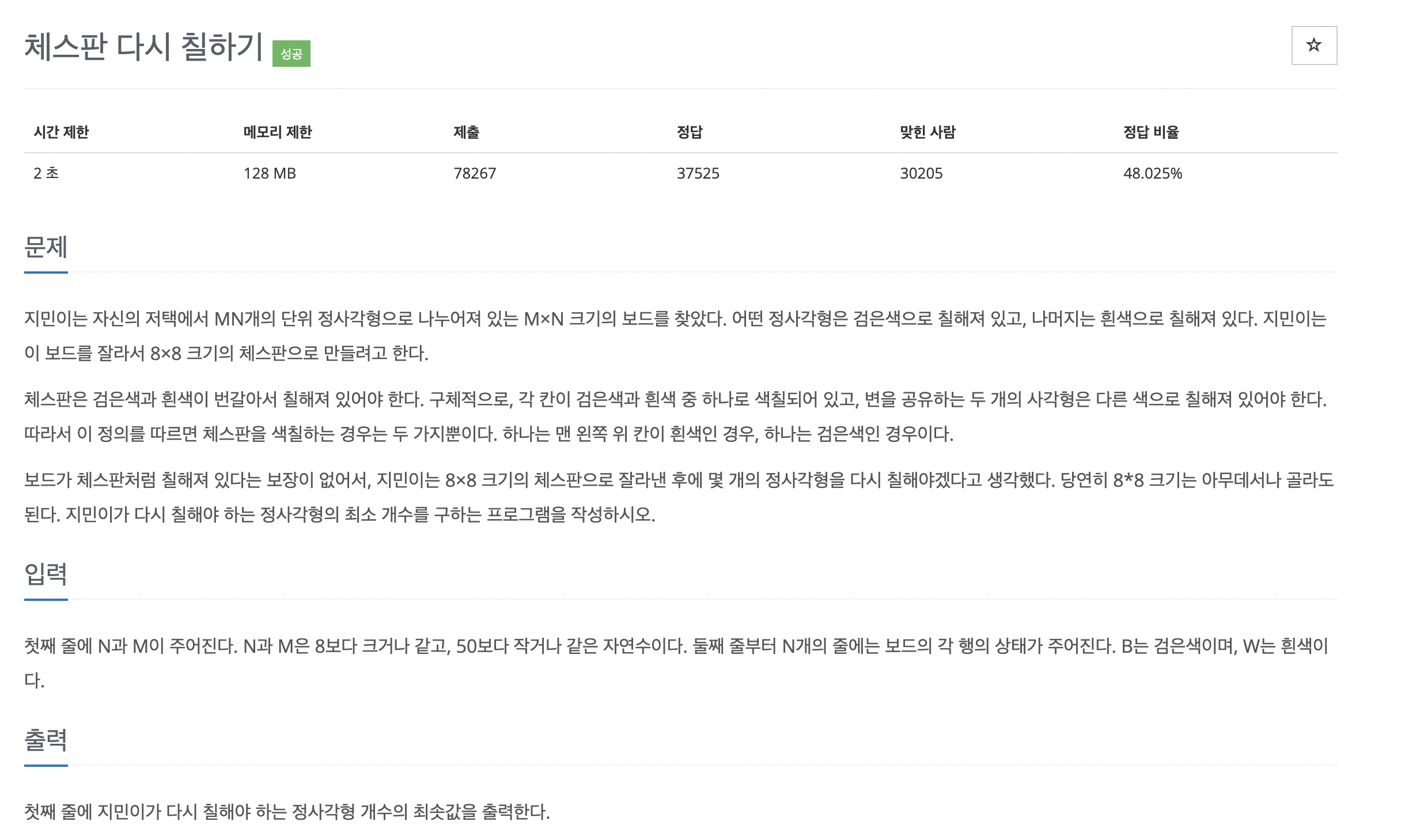
풀이 과정

이 문제를 보고 처음 생각한 건 최솟값 구하기니까 DFS, BFS, 완전 탐색, DP 이 쪽이 아닐까 했다.

근데 아무리봐도 다른 알고리즘을 적용할 수 없을 거 같아서
설마 완전 탐색인가 의심이 들어서 연산횟수를 계산했다.

50x50이 최대 크기고 8개를 맞춰야하니 마지막 7개 행,열은 빼면
대충 43x43 = 1849 정도의 굉장히 적은 연산횟수를 가진다.

그리고 추가적으로 8x8 행렬에서 체스판이랑 얼마나 다른 지 비교해야되니까
1849*64 = 118336 정도의 연산횟수를 가진다고 생각했다.
5억번 정도 미만이면 완전탐색으로 풀어도 시간초과가 안난다는 글을 봤기 때문에 충분하지 않을까? 했다.

근데 아무래도 완전탐색을 지양하자는 생각이 있어서 그런 지
계속 진짜 맞나..? 다른 방법은 없나..? 하고 시간 낭비를 했다.

결국 밑에 힌트를 보고 브루트포스라고 적혀있어서 아.. 완전탐색 맞구나.. 했다.

알고리즘

아래를 반복한다.
1. 처음부터 옆으로, 아래로 이동해가면서 8x8행렬을 만든다.
2. 만든 8x8 행렬과 실제 체스판을 비교해서 다른 부분의 개수를 센다.
가장 다른 부분이 적었던 횟수를 출력한다.

최종 코드

n, m = map(int, input().split())

matrix = []


for i in range(n):
    matrix.append(list(input()))

# 8x8에서 나올 수 있는 올바른 체스판 종류 - 제일 첫번째 색이 검정색인 체스판
black_started_chess = [
    "BWBWBWBW",
    "WBWBWBWB",
    "BWBWBWBW",
    "WBWBWBWB",
    "BWBWBWBW",
    "WBWBWBWB",
    "BWBWBWBW",
    "WBWBWBWB",
]

# 8x8에서 나올 수 있는 올바른 체스판 종류 - 제일 첫번째 색이 흰색인 체스판
white_started_chess = [
    "WBWBWBWB",
    "BWBWBWBW",
    "WBWBWBWB",
    "BWBWBWBW",
    "WBWBWBWB",
    "BWBWBWBW",
    "WBWBWBWB",
    "BWBWBWBW",
]

# 최소 색칠 횟수
min_coloring_count = 1e9

# 8x8행렬을 만들 수 있는 가짓 수 대로 만듦
for i in range(n - 7):
    for j in range(m - 7):
    	
        # 만들어진 8x8 행렬
        temp_chess = [lst[j : j + 8] for lst in matrix[i : i + 8]]
		
        # 첫번째가 검정색인 체스판과 다른 부분
        black_count = 0
        
        # 첫번째가 흰색인 체스판과 다른 부분
        white_count = 0
		
     	# 8x8 행렬이 체스판과 얼마나 다른 지 비교
        for k in range(8):
            for l in range(8):
            	# 첫번째가 흰색인 체스판과 지금 이 행렬에 다른 부분이 있으면
                if temp_chess[k][l] != white_started_chess[k][l]:
                	# white_count 1증가
                    white_count += 1
				
                # 첫번째가 검정색인 체스판과 지금 이 행렬에 다른 부분이 있으면
                if temp_chess[k][l] != black_started_chess[k][l]:
                	# black_count 1증가
                    black_count += 1
                    
		# 둘 중에서 최솟값으로 min_count 설정
        min_count = min(black_count, white_count)
		
        # 만들 수 있는 모든 행렬에서 최솟값이 되도록 min_coloring_count를 업데이트
        if min_count < min_coloring_count:
            min_coloring_count = min_count

print(min_coloring_count)

결과는 통과

주석 없는 코드

n, m = map(int, input().split())

matrix = []


for i in range(n):
    matrix.append(list(input()))

black_started_chess = [
    "BWBWBWBW",
    "WBWBWBWB",
    "BWBWBWBW",
    "WBWBWBWB",
    "BWBWBWBW",
    "WBWBWBWB",
    "BWBWBWBW",
    "WBWBWBWB",
]

white_started_chess = [
    "WBWBWBWB",
    "BWBWBWBW",
    "WBWBWBWB",
    "BWBWBWBW",
    "WBWBWBWB",
    "BWBWBWBW",
    "WBWBWBWB",
    "BWBWBWBW",
]

min_coloring_count = 1e9

for i in range(n - 7):
    for j in range(m - 7):
        temp_chess = [lst[j : j + 8] for lst in matrix[i : i + 8]]

        black_count = 0
        white_count = 0

        for k in range(8):
            for l in range(8):
                if temp_chess[k][l] != white_started_chess[k][l]:
                    white_count += 1

                if temp_chess[k][l] != black_started_chess[k][l]:
                    black_count += 1

        min_count = min(black_count, white_count)

        if min_count < min_coloring_count:
            min_coloring_count = min_count

print(min_coloring_count)

다른 사람의 풀이

n, m = map(int, input().split())
board = []
result = []
 
for _ in range(n):
    board.append(input())
 
for i in range(n-7):
    for j in range(m-7):
        draw1 = 0
        draw2 = 0
 
        for a in range(i, i+8):
            for b in range(j, j+8):
                if (a + b) % 2 == 0:
                    if board[a][b] != 'B':
                        draw1 += 1
                    if board[a][b] != 'W':
                        draw2 += 1
                else:
                    if board[a][b] != 'W':
                        draw1 += 1
                    if board[a][b] != 'B':
                        draw2 += 1
 
        result.append(draw1)
        result.append(draw2)
 
print(min(result))