[백준 BOJ] 1003 : 피보나치 함수 - python

오늘 풀어볼 문제는 피보나치 함수이다.

문제

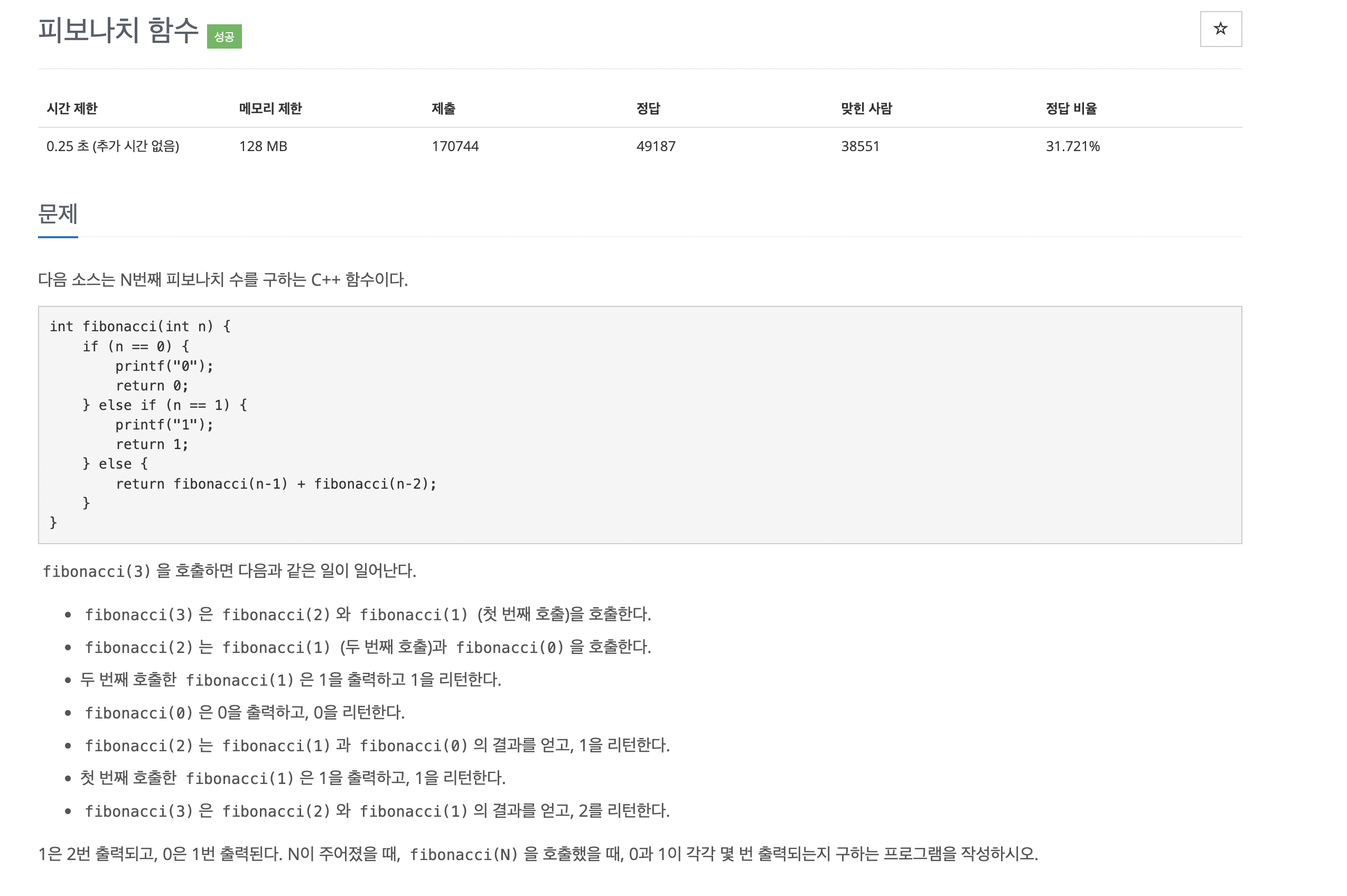
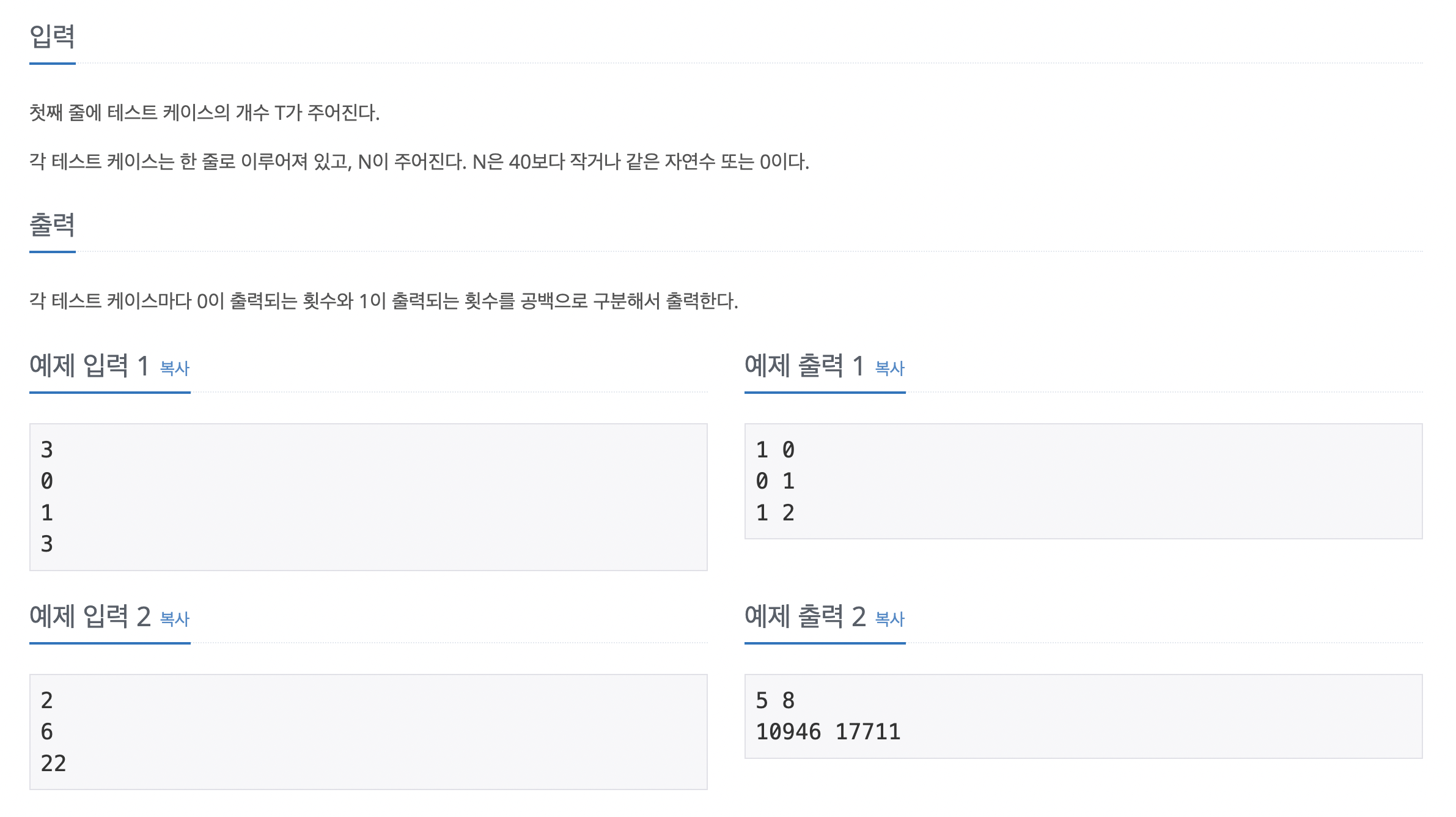
풀이 과정

이 문제를 보고 처음 생각한 건 혹시 dp..? 였다.
시간이 0.25초로 매우 짧기 때문에 절대로 재귀로 구현하면 안될거고
피보나치 수열에서 구하는 시간 단축하는 유명한 방법은 dp니까 말이다.
그리고 dp테이블을 한 번 구해 놓으면 테스트 케이스가 여러개 나오니까 다음 케이스에서도 재활용할 수도 있다.

그래서 dp 문제구나 하고 dp로 풀었다.

알고리즘

dp 문제를 풀 때 가장 먼저 할 일은 규칙 찾기다.
그래서 공책에 끄적여 보면서 규칙을 찾아 봤다.

	0 개수	1개수	fibo(n)
fibo(0)	1	0	0
fibo(1)	0	1	1
fibo(2)	1	1	1
fibo(3)	1	2	2
fibo(4)	2	3	3

이 쯤 하면 규칙이 보인다.

fibo(n)에서 0을 출력하는 횟수 = fibo(n-2)의 0 출력 횟수 + fibo(n-1)의 0 출력 횟수

즉 fibo(n)에서 0을 출력하는 횟수를 저장하는 리스트를 zero_count라고 하면

zero_count[i] = zero_count[i-2] + zero_count[i-1]

이라는 점화식을 세울 수 있다.
1을 출력하는 횟수를 구할 때도 마찬가지로 동작한다.

이 점화식을 토대로 dp를 사용해 bottom-up 방식으로 풀었다.

최종 코드

dp = [-1] * 41
zero_count = [0] * 41
one_count = [0] * 41

dp[0] = 0
dp[1] = 1

zero_count[0] = 1
one_count[1] = 1


def fibo(n):
    if dp[n] != -1:
        return

    for i in range(2, n + 1):
        dp[i] = dp[i - 2] + dp[i - 1]
        zero_count[i] = zero_count[i - 2] + zero_count[i - 1]
        one_count[i] = one_count[i - 2] + one_count[i - 1]


t = int(input())

for i in range(t):
    n = int(input())

    fibo(n)

    print(zero_count[n], one_count[n])

결과는 통과
근데 다 풀고 생각해보니 굳이 피보나치 값 저장을 위해서 dp라는 배열을 둘 필요는 없을 거 같다.

다른 사람의 풀이

t = int(input())
 
for _ in range(t):
    cnt_0 = [1,0]
    cnt_1 = [0,1]
    n = int(input())
    if n>1:
        for i in range(n-1):
            cnt_0.append(cnt_1[-1])
            cnt_1.append(cnt_0[-2]+cnt_1[-1]) 
 
    print(cnt_0[n], cnt_1[n])

거의 똑같은데 dp테이블을 미리 선언해주지 않고 append 해나갔다는 점이 다르다.
사실 나도 원래는 이렇게 구현하는 걸 선호하는데 top-down으로 풀려고
dp테이블을 미리 선언해 놨는데 중간에 bottom-up으로 바꿨어서 깜빡했다.