1. 알고리즘(Algorithm)
알고리즘(Algorithm)
문제를 해결하기 위해 정해진 진행 절차나 방법을 말한다.
컴퓨터에서 알고리즘은 어떠한 행동을 하기 위해서 만들어진 프로그램 명령어의 집합이다.
알고리즘은 특정 문제를 해결하기 위한, 일련의 명확하고 유한한 단계적 절차 또는 계산 과정을 말한다.
즉 프로그래머는 이러한 문제 해결의 과정을 코드로 작성하여 컴퓨터에 명령어로 보내줘야 하는 것이다.
이러한 알고리즘을 구현할 때에는 바로 코드를 짜는 것보다 의사 코드 혹은 플로우차트를 먼저 그리는 것이 좋다.
-
의사코드 - pseudo-code(슈도코드)
알고리즘을 표현하는 방법 중 하나로, 일반적으로는 자연어를 이용해 만든 문장을 프로그래밍 언어와 유사한 형식으로 배치한 코드를 뜻한다. 용도는 미술의 스케치와 같다. -
플로우차트(흐름도, 순서도) 활용
알고리즘 조건
1. 입력 : 알고리즘은 0개 이상의 입력을 가져야 함
2. 출력 : 알고리즘은 최소 1개 이상의 결과를 가져야 함
3. 명확성 : 수행 과정은 모호하지 않고 정확한 수단을 제공해야 함
4. 유한성 : 수행과정은 무한하지 않고 유한한 작업 이후에 정지해야 함
5. 효과성 : 모든 과정은 명백하게 실행 가능해야 함
2. 재귀
2.1 재귀의 정의
재귀(Recursion)
어떠한 것을 정의할 때 자기 자신을 참조하는 것으로, 함수를 정의할 때 자기 자신을 이용하여 표현하는 방법
재귀는 전의 주말 공부에서 한 번 다뤄 본 적 있는 내용이다. 한 번 더 복습하는 느낌으로 간략하게 요약하고자 한다.
재귀함수의 조건
-함수 내용 중 자기 자신 함수를 다시 호출할 것.
-종료 조건이 있어야 할 것.
2.2 재귀함수의 사용 - 팩토리얼 함수
재귀함수의 대표적인 사용 예시인 팩토리얼 함수에 대해 다뤄보고자 한다.
- Factorial : 정수를 1이 될때까지 차감하여 곱한 값
x! = x * ( x - 1 )!;
1! = 1;
static int Factorial(int x)
{
if(x == 1)
return 1;
else
return x + Factorial(x - 1);
}팩토리얼 함수에 x를 대입하면 x 와 Factorial(x-1)을 반환하며, 1까지 계속해서 반환해주게 된다.
2.3 재귀함수의 장단점
- 재귀함수 장점
- 코드로 표현하기 어려운 경우도 직관적으로 처리가 가능
- 분할정복을 통한 반절 계산이 가능해서 효율이 높아지게 구현이 가능
- 재귀함수 단점
알고리즘 구현이 어려움
3. 정렬 알고리즘
- 정렬 알고리즘
특정 배열이나 콜렉션을 넘겨주고, 해당 컨테이너를 오름차순이나 내림차순으로 정렬시킬 때, 구현하는 방법
이런 정렬 알고리즘은 구현 방법이 다양하고 각각의 장단점이 있다.
아래에서 해당 방법에 대한 공부 및 직접 구현을 시도해 보았다.
* 들어가기 전, 참고하기 유용한 사이트
(정렬 알고리즘, 그래프 등 알고리즘 관련 시각 자료 모음 사이트)
https://www.cs.usfca.edu/~galles/visualization/Algorithms.html
3.1 선택 정렬
- 선택정렬
데이터 중 가장 작은 값부터 하나씩 선택하여 정렬하는 방식이다.
 해당 방법에 대해 슈도 코드를 써 봤을 때 아래와 같이 작성하였다.
해당 방법에 대해 슈도 코드를 써 봤을 때 아래와 같이 작성하였다.
- 자료 전체 중에 제일 작은 값을 찾는다.
- 해당 자료를 제일 앞으로 위치를 바꾼다.
- 다음으로 작은 자료를 찾는다.
- 해당 자료를 두 번째 칸에 위치를 바꾼다.
- 위와 같이 계속해서 작은 값을 찾으면서 순차적으로 줄을 세운다.
이와 같은 방식으로 코드를 작성해보자. 우선 '위치를 바꾼다' 라는 부분을 구현하기 위해서 Swap 함수부터 만들어보기로 했다.
public static void Swap(int[] array, int left, int right)
{
int temp = array[left];
array[left] = array[right];
array[right] = temp;
}
// 리스트 형식으로도 만들어보려고 리스트 Swap 함수도 만들었다.
public static void Swap<T>(List<T> list, int left, int right)
{
T temp = list[left];
list[left] = list[right];
list[right] = temp;
}여기까지 만들고, 이제는 작은 값을 찾아낼 방법만 찾으면 된다. 사실 작은 값을 찾아내는 함수는, for 문을 이용하면 쉽게 만들 수 있을 것 같았다. For문 두 개를 중첩해서 선택정렬 알고리즘을 만들어 보았다.
// 배열 버전
public static void SelectionSort(int[] array)
{
for (int i = 0; i < array.Length; i++)
{
int minIndex = i;
for (int j = i; j < array.Length; j++)
{
if (array[minIndex] > array[j])
{
minIndex = j;
}
}
Swap(array, i, minIndex);
}
}
// 리스트 버전
public static void SelectionSort2(List<int> list)
{
for(int i = 0; i < list.Count; i++)
{
int minIndex = i;
for(int j = i; j <list.Count; j++)
{
if (list[minIndex] > list[j])
{
minIndex = j;
}
}
}
}선택 정렬 알고리즘의 빅오
| 시간복잡도 | 공간복잡도 |
|---|---|
| O(n²) | O(1) |
3.2 삽입 정렬
- 삽입정렬
데이터를 하나씩 꺼내어 정렬된 자료 중 적합한 위치에 삽입하여 정렬
- 선택 정렬은 제일 작은 값을 찾아야 한다.
- 삽입 정렬은 특정 값을 정하고, 그 값과 주변 값을 비교해서 어디에 들어가야 하는지 찾아내는 정렬법이다.
이와 같은 점을 유념하고 슈도 코드를 작성해보자.
- 자료 중 특정 값을 정한다. ( 쉽게, 그냥 맨 앞 바로 뒤의 수를 타겟으로 고른다. )
- 해당 자료를 바로 앞의 값과 비교해서, 앞의 값이 크면 Swap 한다.
- 해당 자료가 Swap을 할 수 없을 때까지 비교를 한 후, 다음 값에 대해 똑같은 과정을 진행한다.
선택 정렬에서 사용했던 Swap 함수를 같이 사용해서 삽입정렬의 알고리즘을 만들어보았다.
배열 버전
public static void InsertionSort(int[] array)
{
for(int i = 1; i < array.Length; i++)
{
for(int j = i; j > 0; j--)
{
if (array[j-1] > array[j])
{
Swap(array, j-1, j);
}
}
}
}
// 리스트 버전
public static void InsertionSort2(List<int> list)
{
for (int i = 1; i < list.Count; i++)
{
for (int j = i; j > 0; j--)
{
if (list[j-1] > list [j])
{
Swap(list, j-1, j);
}
}
}
}
#endregion부등호에서 숫자 하나 잘못 들어가면 바로 정렬이 이상해졌기 때문에 의외로 구현하는 데 고생했다.
삽입 정렬 알고리즘의 빅오
| 시간복잡도 | 공간복잡도 |
|---|---|
| O(n²) | O(1) |
3.3 버블 정렬
- 버블 정렬
서로 인접한 데이터를 비교하여 정렬하는 방식이다
영상처럼 거품이 올라오는 것처럼, 큰 숫자부터 정렬된다고 해서 버블 정렬이라고 한다.
(여기서부터는 배열 버전, 리스트 버전 따로 만드는 게 그다지 의미가 없을 것 같아 배열로만 작성하였다.)
마찬가지로 슈도 코드를 작성해보자.
- 자료 중 특정 값을 정한다. ( 쉽게, 그냥 맨 앞의 수를 타겟으로 고른다. )
- 해당 자료를 바로 뒤의 값과 비교해서, 뒤의 값이 크면 Swap 한다.
- 해당 자료가 Swap을 할 수 없을 때까지 비교를 한 후, 다음 값에 대해 똑같은 과정을 진행한다.
선택 정렬에서 사용했던 Swap 함수를 같이 사용해서 삽입정렬의 알고리즘을 만들어보았다.
public static void BubbleSort(int[] array)
{
for(int i = 1; i < array.Length; i++)
{
for (int j = 0; j < array.Length - 1; j++)
{
if (array[j] > array[j + 1])
{
Swap(array, j, j + 1);
}
}
}
}버블 배열은 작성해보니 삽입 정렬의 역순 느낌으로 제작하면 될 것 같아 생각보다 쉽게 구현하였다.
버블 정렬 알고리즘의 빅오
| 시간복잡도 | 공간복잡도 |
|---|---|
| O(n²) | O(1) |
3.4 병합 정렬
- 병합정렬 / 합병정렬
데이터를 2분할하여 정렬 후 병합하는 방식이다.
 해당 알고리즘 진행 방식이 잘 이해가 되지 않을 수도 있는데, 좀 더 상세히 설명하자면 아래와 같다.
해당 알고리즘 진행 방식이 잘 이해가 되지 않을 수도 있는데, 좀 더 상세히 설명하자면 아래와 같다.
- 데이터를 2분할을 한다. 그 나눠진 데이터를 또 2분할 하고, 계속해서 2분할을 하다 보면 결국 데이터는 하나만 남을 것이다. 그러면 그 각각 남은 데이터는 앞 뒤로 비교해서 정렬하고, 2개의 묶음이 된 정렬데이터는 또 2개의 묶음의 정렬과 비교하여 정렬한다.
이런 식으로 데이터를 잘게 나눈 뒤에 그 데이터들을 정렬하면서 결합하는 방식이다.
여기서부터는 확실히 구현 난이도가 올라가는 것을 느꼈다.
코드를 짤 때 어떻게 짜야 할까. 슈도 코드를 작성해 보았다.
- 우선은 데이터를 나눠야 한다. 컴퓨터에서 나누기는 몫을 반환하니, 나누기를 계속 해서 데이터를 잘게 쪼개주자
1.1) 나누기를 몇 번 해야 할까? 이 나누기 연산을 구현하기 위해서 재귀를 사용하겠다.
1.2) 재귀를 사용한다 하면, 종료를 위한 조건이 필요할 것이다. 종료를 위한 조건은, 나눠야 할 대상의 몫이 1이 되었을 때로 한다.
- 무수히 나누고 난 뒤의 배열을 정렬해 주자.
2.1 배열의 정렬 조건은 start, mid, end 기준으로, start ~ mid 정렬을 하고, mid ~ end 정렬을 한다. 그 다음으로 전체 정렬을 한다.
public static void MergeSort(int[] array) => MergeSort(array, 0, array.Length-1);
public static void MergeSort(int[]array, int start, int end)
{
if (start == end)
return;
int mid = (start + end) / 2;
MergeSort(array, start, mid);
MergeSort(array, mid + 1, end);
Merge(array, start, mid, end);
}
public static void Merge(int[] array, int start, int mid, int end)
{
List<int> sortedList = new List<int>();
int leftIndex = start;
int rightIndex = mid + 1;
while(leftIndex <= mid && rightIndex <= end)
{
if (array[leftIndex] < array[rightIndex])
{
sortedList.Add(array[leftIndex]);
leftIndex++;
}
else
{
sortedList.Add(array[rightIndex]);
rightIndex++;
}
}
if(leftIndex <= mid)
{
while(leftIndex<=mid)
{
sortedList.Add(array[leftIndex]);
leftIndex++;
}
}
else
{
while(rightIndex<=end)
{
sortedList.Add(array[rightIndex]);
rightIndex++;
}
}
for (int i = 0; i<sortedList.Count; i++)
{
array[start + i] = sortedList[i];
}
}처음엔 리스트를 사용한다는 생각에 닿지 못했고, 까딱 부등호 잘못 쓰면 결과가 이상해지는 탓에 코드 작성에서 많은 수난이 있었다.
병합 정렬 알고리즘의 빅오
| 시간복잡도 | 공간복잡도 |
|---|---|
| O(nlogn) | O(n) |
특아히게 병합 정렬의 경우 공간 복잡도가 O(n)으로 되어 있는데, 이는 위의 영상에서 보다시피 병합 정렬은 추가적인 공간에 데이터를 복사한 후 정렬하고 있기 때문에 공간복잡도 효율이 떨어지는 특성이 있다.
3.5 퀵 정렬
- 퀵 정렬
하나의 기준(피벗)으로 작은 값과 큰 값을 2분할하여 정렬하는 방식
위에서 설명했던 병합 정렬과 조금 유사하면서도 다른 방식이다. 방식에 대해 상세 설명하자면 다음과 같다
- 특정 값을 Pivot으로 설정하고, 그 값을 기준으로 큰 값과 작은 값을 분류한다. 그리고 그 Pivot을 분류한 두 값들 사이에 정렬하고, 분할된 두 값들에서 다시 Pivot을 골라 정렬한다. 이와 같은 과정을 반복하여 전체 데이터를 정렬한다.
Pivot을 골라 큰 값과 작은 값으로 분리하는 작업을 '반복'한다고 했으니, 재귀를 써야 한다는 생각이 들었다. 해당 알고리즘의 슈도 코드를 작성해 보자.
- 피봇을 고른다.(피봇은 맨 앞의 값, start로 하면 될 것이다.)
- 피봇을 기준으로 값이 작으면 왼쪽에, 값이 크면 오른쪽에 값을 넣는다.(Swap을 사용하겠다)(정렬 X)
- 이와 같은 과정으로 분리된 두 영역 사이에 피봇을 넣고, 나눠진 두 영역에 각각 피봇을 만들고 분리 작업을 반복한다.
- 이와 같은 작업을 반복하면 최종적으로 모든 값이 정렬될 것이다.
슈도 코드는 이렇게 작성했으나, 막상 실제로 만들어보니 제작하기 상당히 어려웠다.
public static void QuickSort(int[] array) => QuickSort(array, 0, array.Length - 1);
public static void QuickSort(int[] array, int start, int end)
{
if (start >= end)
return;
int pivot = start;
int left = pivot + 1;
int right = end;
while (left <= right)
{
while (array[pivot] >= array[left] && left < right)
{
left++;
}
while (array[pivot] < array[right] && left <= right)
{
right--;
}
if (left < right)
{
Swap(array, left, right);
}
else
{
Swap(array, pivot, right);
break;
}
}
QuickSort(array, start, right - 1);
QuickSort(array, right + 1, end);
}슈도 코드를 쓴 시점에서 파악하지 못한 점을 몇 가지 짚어 보려고 한다.
- 피봇 기준으로 좌 우를 판정하기 위해서 left, right 변수를 사용한다.
- 피봇 기준으로 큰 값과 작은 값이 다 분리되었다고 판정할 시점은 언제인가? left와 right가 교차되었을 때이다.
- 정렬이 완료되었을 때 피봇을 어떻게 분리된 값 사이에 넣을 것인가? right와 pivot의 위치를 Swap한다.
이와 같은 과정으로 많은 우여곡절을 겪은 끝에 코드를 완성하였다.
퀵 정렬 알고리즘의 빅오
| 시간복잡도 | 공간복잡도 |
|---|---|
| 평균 : O(nlogn) / 최악 : O(n²) | O(1) |
여기서 최악의 경우 O(n²) 인 이유가 뭔지 추가로 말해보고자 한다.
최악의 경우의 예시로, 이미 정렬된 데이터에 퀵 정렬을 시도했다고 해 보자. 그러면 아래와 같이 아주 오래 걸리는 과정을 볼 수 있다.
이와 같이 퀵 정렬에서의 최악의 시나리오는, 피봇의 설정으로 너무 끝 값이 몰려 있다든지의 상황에서 연산이 매우 오래 걸릴 수도 있다는 것이다. 이로 인해 평균으로는 좋은 성능을 보여주는 퀵 정렬이, 특정 상황에서 상당한 연산 속도의 차이를 보일 수도 있다.
3.6 힙 정렬
해당 알고리즘은 대략적인 원리와 코드만 살펴보고 넘어가기로 한다.
- 힙정렬
힙을 이용하여 우선순위가 가장 높은 요소가 가장 마지막 요소와 교체된 후 제거되는 방법을 이용

대략적인 원리를 설명하자면, 위 영상과 같이 토너먼트 형식으로 값을 비교하여 정렬하는 방식이다.
public static void HeapSort(int[] array)
{
MakeHeap(array);
for (int i = array.Length - 1; i > 0; i--)
{
Swap(array, 0, i);
Heapify(array, 0, i);
}
}
private static void MakeHeap(int[] array)
{
for (int i = array.Length / 2 - 1; i >= 0; i--)
{
Heapify(array, i, array.Length);
}
}
private static void Heapify(int[] array, int index, int size)
{
int left = index * 2 + 1;
int right = index * 2 + 2;
int max = index;
if (left < size && array[left] > array[max])
{
max = left;
}
if (right < size && array[right] > array[max])
{
max = right;
}
if (max != index)
{
Swap(array, index, max);
Heapify(array, max, size);
}
}힙 정렬 알고리즘의 빅오
| 시간복잡도 | 공간복잡도 |
|---|---|
| O(nlogn) | O(1) |
힙 정렬은 시간복잡도도 좋고 공간 복잡도도 좋은 이상적인 알고리즘으로 비칠 수도 있다. 하지만 실상 따져 보면, 힙 정렬은 퀵 정렬이나 병합 정렬에 비해 평균적으로 느린 속도를 가지고 있다.
왜 같은 시간복잡도인데도 이런 차이가 발생하는지 설명하자면, 메모리는 데이터를 가져올 때 캐시 메모리로 인접한 영역의 데이터를 같이 긁어 오는 특성이 있다. 따라서 이런 인접한 값의 정렬을 하는 방식이 메모리 면에서도 이득인 상황이 많은데, 힙 정렬은 정렬된 데이터가 인접하게 모이지 않는 경우가 많다.
따라서 캐시 메모리 친화적인 알고리즘은 아니라서 오히려 연산 시간이 더 오래 걸리는 경우가 많다.
4. 정렬 알고리즘을 알아야 하는 이유
이와 같이 다양한 정렬 알고리즘을 배워봤다.
하지만 이러한 것들을 쓰기는 해도, 이렇게 원리까지 알아야 하는지에 대한 의문이 생길 수도 있다.
4.1 유니티의 정렬 알고리즘
단적으로 와 닿을 수 있도록, 앞으로 배워야 할 유니티의 정렬 알고리즘을 들여다 보자.
Unity의 기본 정렬 알고리즘: 인트로소트(Introsort)
Unity는 .NET 프레임워크를 기반으로 동작하며, 컬렉션의 정렬을 위해 .Sort() 메소드를 제공한다. 이 메소드는 내부적으로 인트로스펙티브 정렬(Introspective Sort), 줄여서 인트로소트(Introsort) 알고리즘을 사용한다. 인트로소트는 퀵정렬, 힙정렬, 삽입정렬을 결합한 하이브리드 알고리즘이다.
위키피디아 참고
유니티는 인트로소트라는 정렬 알고리즘을 사용하며, 해당 정렬 알고리즘은 퀵 정렬, 힙 정렬, 삽입 정렬을 같이 사용하고, 자료가 16개 이하일 때는 삽입 정렬, 일반적인 경우에는 퀵 정렬, 퀵 정렬의 효율이 최악일 때 힙 정렬을 사용하는 방식을 채택한다.
그러면 결국엔 실제로 사용하게 될 퀵 정렬, 힙 정렬, 삽입 정렬만 알면 되지 않냐 생각할 수도 있지만, 실상에서는 이 외의 방법을 써야 할 상황이 있다.
4.2 정렬 안정성
다음과 같은 상황을 생각해보자.
게임에서 구현한 랭킹 시스템이 있다고 하자.
랭킹 시스템에서 1차로 레벨 별로 정렬이 되어 있었다고 했을 때, 여기에서 추가로 직업별로 랭킹을 정렬하려고 할 때, 정렬 프로그램을 돌리면 레벨이 높은 순으로 직업별 랭킹이 정렬되도록 하고 싶다.
하지만 실제로 모든 정렬 알고리즘이 다른 조건으로 정렬된 데이터를 다시 다른 조건으로 정렬하게 하면, 기존 정렬을 흐뜨러뜨리지 않을까?
이에 대해서 생각해 보면서, 우리는 정렬 안정성에 대해 알아봐야 한다.
단적으로 아래 상황과 같은 일이 벌어질 수 있는 것이다.
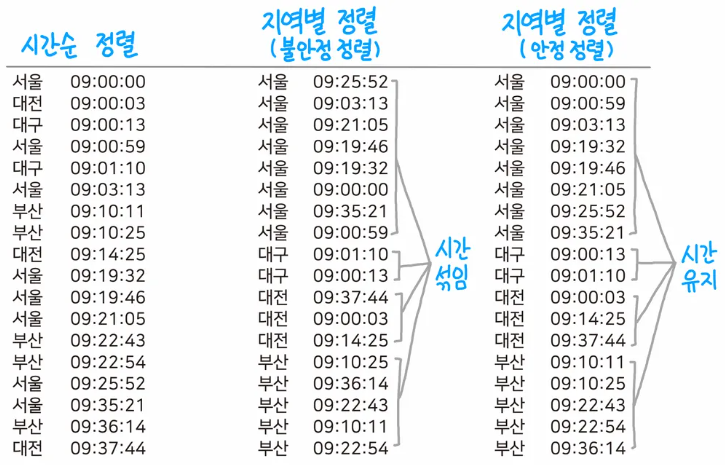
1차적으로 시간순으로 정렬한 데이터를 다시 지역별로 정렬시켰을 때, 시간이 섞이지 않으면 안정 정렬, 섞이면 불안정 정렬이다. 이런 안정 정렬, 불안정 정렬로 다시 위의 정렬 알고리즘을 분류했을 때 아래와 같이 분류된다.
- 안정 정렬
- 삽입 정렬
- 버블 정렬
- 병합 정렬
- 불안정 정렬
- 선택 정렬
- 퀵 정렬
- 힙 정렬
유니티의 정렬 시스템은 기본적으로 속도에 치중하고 있기 때문에 불안정 정렬 방식을 주로 택하고 있는 것을 알 수 있다. 하지만 유니티의 정렬 시스템만으로는 우리가 원하는 시스템을 구현하기 어려울 수도 있다는 점을 알아야 한다. 당장 위와 같은 상황에서도 게임에서 필요한 정렬 시스템이 안정 정렬 시스템이므로, 직접 구현해야 하는 상황이 올 수도 있는 것이다.
이와 같은 점을 유념하여 정렬 알고리즘에 대한 원리를 유념하도록 하자.
참고자료
(정렬안정성 사진자료)
https://velog.io/@stresszero/Sorting-Algorithm