1 선형 탐색 알고리즘
일반적인 자료형을 탐색하기 위한 알고리즘이다.
1.1) 순차 탐색 알고리즘
순차 탐색
자료구조에서 순차적으로 찾고자 하는 데이터를 탐색하는 방식
시간복잡도 - O(n)
처음부터 타겟이 되는 데이터를 찾을 때까지 순차적으로 찾는 방법이다. 목표 데이터를 찾는 데에 시간이 걸릴 수밖에 없으나, 정렬되지 않은 데이터에서 사용할 수 있는 방식이다.
* 순차 탐색 알고리즘 예시 - 타겟 숫자 찾기
public static int LinearSearch(int[] array, int target)
{
for(int i = 0; i < array.Length; i++)
{
if (array[i] == target)
{
return i;
}
}
return -1;
}
static void Main(string[] args)
{
int[] array = { 0, 2, 4, 6, 8, 9, 7, 5, 3, 1 };
int findindex = LinearSearch(array, 9);
Console.WriteLine($"탐색 결과 : {findindex}"); // 5 출력
}1.2) 이진 탐색 알고리즘
이진 탐색
정렬이 되어있는 자료구조에서 2분할을 통해 데이터를 탐색하는 방식
단, 이진 탐색은 정렬이 되어 있는 자료에만 적용 가능하다.
시간복잡도 - O(logn)
업 다운 게임처럼 자료를 찾는 방식이다. 중간 지점에서의 데이터가 목표 데이터보다 큰 값일 경우 아래 부분만 체크하고, 아니면 위쪽 부분만 체크하는 식으로 탐색 영역을 소거한다.
이와 같은 특성 때문에 정렬된 데이터가 아니면 데이터를 찾을 수 없다.
public static int BinarySearch(int[] array, int target)
{
int low = 0;
int high = array.Length - 1;
while (low <= high)
{
int mid = (low + high) / 2;
if (array[mid] > target)
{
high = mid - 1;
}
else if (array[mid] < target)
{
low = mid + 1;
}
else
{
return mid;
}
}
return -1;
}2. 비선형 탐색 알고리즘
비선형 탐색 알고리즘은 그래프와 트리와 같이 비선형적 데이터를 탐색하는 알고리즘이다.
길찾기 알고리즘에 쓰이는 개념으로 BFS, DFS, 다익스트라 등이 있다.
2.1 너비 우선 탐색 알고리즘(BFS)
너비 우선 탐색 (Breadth-First Search)
그래프의 분기를 만났을 때 모든 분기들을 탐색한 뒤, 다음 깊이의 분기들을 탐색한다.
큐를 통해 탐색할 수 있다.
우리가 배웠던 큐의 특성으로, 큐는 데이터를 받은 순서대로 반환하므로 출발 지점에서 갈 수 있는 구간의 데이터를 큐에 담은 후 처리하는 방식으로 운영된다. BFS의 경우에는 최단 경로 찾기가 보장되어 있다.
-BFS 설계를 위한 의사 코드
1. 시작하는 노드(0번 노드)는 방문한 것으로 간주한다. 시작하는 노드 기준으로 방문할 수 있는 노드를 큐에 입력한다.
2. 1차적으로 방문할 수 있는 노드는 0번 노드와 연결되어 있다는 반환을 하고, 순차적으로 다음 구간과 연결되어 있는 노드를 확인하고 결과를 반환한다.
3. 위와 같이 연결되어 있으면서 방문하지 않은 노드들을 확인하며 해당 구간을 연결해 최단거리를 찾는다.
public static void BFS(bool[,] graph, int start, out bool[] visited, out int[] parents)
{
int size = graph.GetLength(0);
visited = new bool[size]; // 방문 여부
parents = new int[size]; // 직전 연결 라인
// 아직 못 찾았다는 표시로 visited는 false, parents는 -1로 표기한다.
for(int i = 0; i < size; i++)
{
visited[i] = false;
parents[i] = -1;
}
Queue<int> queue = new Queue<int>();
queue.Enqueue(start);
visited[start] = true;
while(queue.Count > 0)
{
int next = queue.Dequeue();
for(int vertex = 0; vertex < size; vertex++)
{
// 정점이 연결되어 있고, 방문한 적이 없을 경우
if (graph[next,vertex] == true && visited[vertex] == false)
{
queue.Enqueue(vertex);
visited[vertex] = true;
parents[vertex] = next;
}
}
}
}BFS의 장단점은 아래와 같다.
장점 : 최단 경로를 보장함
단점 : 지금 탐색 상황에서 필요하지 않은 정점 데이터도 큐에 보관할 필요가 있다.(데이터 보관량 많음)
-> 이와 같은 특성으로, 일반적으로 그래프에 사용을 선호함
2.2) 깊이 우선 탐색 알고리즘(DFS)
깊이 우선 탐색 (Depth-First Search)
그래프의 분기를 만났을 때 최대한 깊이 내려간 뒤, 분기의 탐색을 마쳤을 때 다음 분기를 탐색한다. 스택을 통해 구현할 수 있다.
스택이 최신 데이터 순으로 데이터를 처리하는 방식처럼, 한 분기의 탐색을 마칠 때까지 들어갔다가 돌아나오는 방식이다. 상황에 따라서는 너비 우선 탐색보다 훨씬 빠르게 최단 경로를 찾을 수 있다.
-DFS 설계를 위한 의사 코드
1. 시작하는 노드(0번 노드)는 방문한 것으로 간주한다. 시작하는 노드 기준으로 방문할 수 있는 노드 중 첫 번째 순서의 노드를 스택에 담고 방문한다.
2. 해당 노드에 이동할 수 있는 다른 분기가 있으면 우선 순위를 두어 해당 노드를 스택에 담고 방문한다.
3. 더 이상 방문할 수 있는 노드가 없을 시 데이터를 반환한다.(Pop)
4. 위와 같은 과정을 반복하여 경로를 찾는다.
DFS는 구현할 수 있는 방법이 두 가지가 있다. 첫째로 함수 호출 스택을 사용하는 방법이다.
public static void DFS(bool[,] graph, int start, out bool[] visited, out int[] parents)
{
int size = graph.GetLength(0);
visited = new bool[size]; // 방문 여부
parents = new int[size]; // 직전 연결 라인
// 아직 못 찾았다는 표시로 visited는 false, parents는 -1로 표기한다.
for (int i = 0; i < size; i++)
{
visited[i] = false;
parents[i] = -1;
}
// 함수 호출 스택을 쓰는 방법
SearchNode(graph, start, visited, parents);
}
public static void SearchNode(bool[,] graph, int vertex, bool[] visited, int[] parents)
{
int size = graph.GetLength(0);
visited[vertex] = true;
for(int i = 0; i < size; i++)
{ // 연결이 되어 있는 정점 방문한 적이 없는 정점
if (graph[vertex, i] == true && visited[i] == false)
{
parents[i] = vertex;
SearchNode(graph, i, visited, parents);
}
}
}그리고 두 번째 방법은 스택을 이용하는 방법인데, 이는 풀이과정을 알려주지 않고 풀어보는 과제로 남겨주셨다. 스택을 통해 직접 구현해 보는 과제를 고민하면서 아래와 같이 의사코드를 짰다.
public static void DFSStack(bool[,] graph, int start, out bool[] visited, out int[] parents)
{
int size = graph.GetLength(0);
visited = new bool[size]; // 방문 여부
parents = new int[size]; // 직전 연결 라인
// 아직 못 찾았다는 표시로 visited는 false, parents는 -1로 표기한다.
for (int i = 0; i < size; i++)
{
visited[i] = false;
parents[i] = -1;
}
// 초기화 부분까지는 그대로 쓰면 될 것 같다. 아래부터 코드를 짜 보자
// 1. 스택을 선언한다.
// 2. 스택에 Push로 초기값(start)를 넣는다
// 3. 처음 방문한 start 노드의 방문 여부를 true로 바꾼다.
Stack<int> stack = new Stack<int>();
stack.Push(start);
visited[start] = true;
while (스택에 0 이상 들어있을 때)
{
for (int i = 0; i < size; i++)
{
// 스택에 들어 있는 값을 확인하고
if (해당 스택과 비교하여 방문여부가 false, 해당 스택과 연결되어 있을 경우)
{
// 스택에 Push
// 방문 여부 = true
// 부모노드 연결
}
// 더이상 인접한 미방문 노드가 없을 때 Pop으로 스택 데이터 반환
}
}
}이와 같이 생각하여 코드를 마저 작성하여 아래와 같이 작성하였다. 하지만 문제가 생겼다.
...
Stack<int> stack = new Stack<int>();
stack.Push(start);
visited[start] = true;
while (stack.Count > 0)
{
for (int i = 0; i < size; i++)
{
int vertex = stack.Peek();
if (visited[i] == false && graph[vertex, i] == true)
{
stack.Push(i);
visited[i] = true;
parents[i] = vertex;
}
else
{
stack.Pop();
}
}
}
...노드가 연결되지 않을 때마다 Pop으로 스택 데이터가 나가다 보니 스택에 반출할 데이터가 없다는 오류가 걸린 것이다. Pop을 하는 조건을 else로 하면 안 되는 것임을 알게 된 것이다.
그러면 언제 Pop을 해야자 적절할까? 가만 생각해보니, for문을 전부 다 돌리고 나서 Pop을 해야겠단 생각이 들었다.
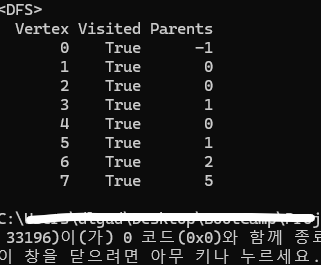와, 잘 실행되었다! 라고 생각하기에는 함정이 있었다. 이 데이터가 맞는지 한 번 검증할 필요가 있었는데, 기존에 만들었던 DFS 코드와 결과를 비교해보니 다음과 같이 출력되었다.
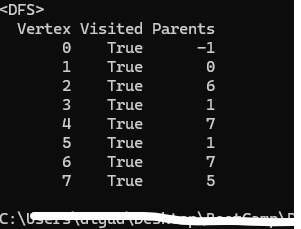
...기존 DFS 코드와 결과가 미묘하게 다르게 출력이 된다. 무슨 문제가 생긴 건지 되짚어보기로 했다.
참고로 결과 출력을 위해 사용한 그래프는 아래와 같다.
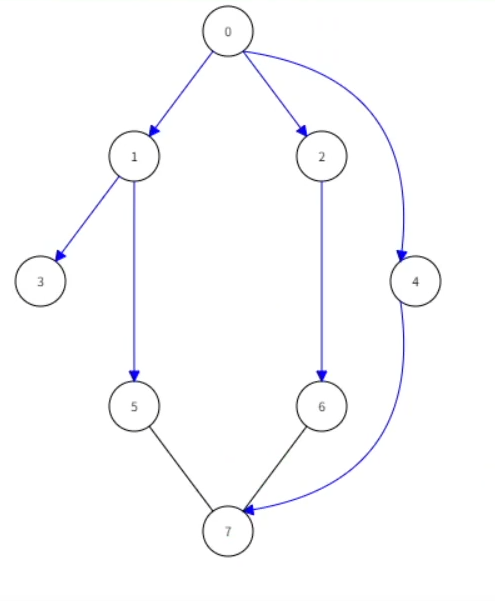
내가 짠 코드와 결과값을 비교해 보면, 무언가가 잘못됐음을 알게 되었다. 왜 7에서 4나 6으로 넘어가지 않고 종료된 거지?
가만 생각해보니 for문에서 7번 노드에 가고 나서 다른 구간으로 가지 않고 종료되는 현상을 발견하였다. 이전 노드와 연결되어 있음에도 for문에서는 종료되고 마니 결과가 달라진 것이다.
그래서, 노드를 들어갈 때마다 i를 초기화 시켜줘야 한다는 사실을 알게 되었다.
- 최종 코드
public static void DFSStack(bool[,] graph, int start, out bool[] visited, out int[] parents)
{
int size = graph.GetLength(0);
visited = new bool[size]; // 방문 여부
parents = new int[size]; // 직전 연결 라인
// 아직 못 찾았다는 표시로 visited는 false, parents는 -1로 표기한다.
for (int i = 0; i < size; i++)
{
visited[i] = false;
parents[i] = -1;
}
Stack<int> stack = new Stack<int>();
stack.Push(start);
visited[start] = true;
while (stack.Count > 0)
{
for (int i = 0; i < size; i++)
{
int vertex = stack.Peek();
if (visited[i] == false && graph[vertex, i] == true)
{
stack.Push(i);
visited[i] = true;
parents[i] = vertex;
i = 0;
}
}
stack.Pop();
}
}
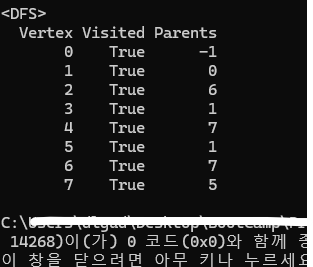
이제 정상적으로 값이 출력되는 것을 확인할 수 있다.
DFS의 장단점은 아래와 같다.
장점 : 지금 탐색 상황에서 필요한 정점 데이터만 보관 가능하고, 탐색이 끝나면 버려도 무관하다. (데이터 보관량 적음)
단점 : 최단 경로를 보장하지 못함
-> 일반적으로 트리에 사용을 선호함 (트리에서는 최단경로가 하나밖에 없으니 무조건 최단경로를 찾게됨-단점이 사라짐)
2.3) BFS vs DFS
위에서 짰던 코드를 바탕으로 BFS와 DFS의 차이를 확인해보고자 한다.
DFS의 결과는 아래와 같았다.
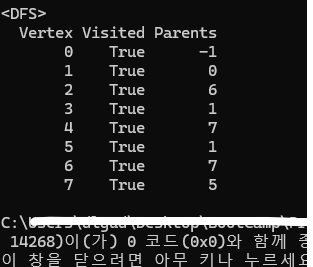
하지만 BFS로 똑같은 그래프의 결과를 도출하면 아래와 같이 나온다.
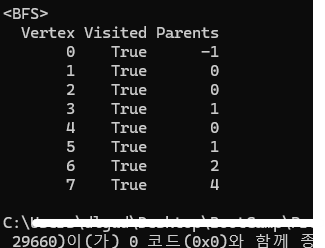
실제로 위에 있는 그래프를 통해 최단 경로를 계산해 보면, BFS가 최단 경로를 계산한 것이고 DFS는 엉뚱한 결과가 도출된 것을 확인할 수 있다.
이와 같은 부분이 DFS 가 도출한 값이 최단거리가 아닐 수도 있다는 점의 단적인 예가 아닐까 싶다.
그런데 그러면 BFS가 무조건 좋다고 말할 수 있을까?
그건 장담할 수 없다.
애초에 두 가지의 경우를 딱 적당한 상황에서 쓸 수 있을지 장담할 수 없는 것이, 그걸 예측하고 쓸 수 있다는 것 자체가 데이터의 위치를 어느 정도 가늠할 수 있다는 소리이기 때문이다.
하지만 실제로는 데이터의 위치를 몰라서 해당 방법을 쓰는 것이기 때문에 순전히 운과 상황에 의해서 결정된다.
물론 데이터의 값이 어디쯤 있을지 예상할 수 있으면 적절한 방법을 사용하겠지만, 이런 부분을 감안해야 할 것이다.
2.4) 다익스트라 알고리즘(Dijkstra Algorithm)
다익스트라 알고리즘
특정한 노드에서 출발하여 다른 노드까지 가는 각각의 최단 경로를 구하는 알고리즘이다.
1. 방문하지 않은 노드 중에서 가장 가까운 노드를 선택한 후,
2. 선택한 노드를 거쳐서 더 짧아지는 경로가 있는 경우 대체된다.
다익스트라에 대한 의사코드는 아래와 같이 작성하였다.
의사코드
1. 시작할 위치에서 갈 수 있는 정점을 확인한다.
2. 갈 수 있는 경로 중 가장 가까운 정점을 선택하여 방문한다.
3. 해당 정점에서 갈 수 있는 정점을 확인하면서 가중치에 따른 최단 경로를 업데이트한다.
4. 방문을 완료한 지점은 더 이상 방문하지 않으며, 방문하지 않은 노드가 없을 때까지 해당 과정을 반복한다.
5. 위의 과정의 결과로 각 정점마다의 최단 거리를 갱신하여, 최단 경로를 알아낼 수 있다.
const int INF = 99999;
public static void Dijkstra(int[,] graph, int start, out bool[] visited, out int[] parents, out int[] cost)
{
int size = graph.GetLength(0);
visited = new bool[size];
parents = new int[size];
cost = new int[size];
for (int i = 0; i < size; i++)
{
visited[i] = false;
parents[i] = -1;
cost[i] = INF;
}
cost[start] = 0;
for (int i = 0; i < size; i++)
{
int minIndex = -1;
int mincost = INF;
for (int j = 0; j < size; j++)
{
if (visited[j] == false && cost[j] < mincost)
{
minIndex = j;
mincost = cost[j];
}
}
if (minIndex < 0)
break;
visited[minIndex] = true;
for (int j = 0; j < size; j++)
{
if (cost[j] > cost[minIndex] + graph[minIndex, j])
{
cost[j] = cost[minIndex] + graph[minIndex, j];
parents[j] = minIndex;
}
}
}
}