(출처) https://www.algospot.com/judge/problem/read/FANMEETING
완전탐색의 경우
주어진 아이돌 멤버의 수를 N, 팬의 수를 N'라고 할 때 필요한 총 검사 횟수는 N' - N + 1 번이다. 또한 매번 검사 시 N 번의 배열탐색이 일어난다. 따라서 시간복잡도는 O(N*N' - N^2 + N)으로 만약 팬의 수가 20만, 아이돌 멤버의 수가 1만이 입력으로 들어왔을 때 완전탐색으로는 대략 20억 정도의 계산이 필요하게된다. 시간제한은 10초이므로 시간초과가 예상되는 범위이다.
더 빠른 알고리즘 계산
아무리 생각해도 더 빠르게 할만한 방법을 찾지 못해 결국 포기하고 답변을 찾아봄. 결론부터 말하자면 해당 문제는 곱셈변형을 통한 카라츠바 알고리즘을 사용하여 N^lg3 속도의 시간복잡도로 해결할 수 있다.
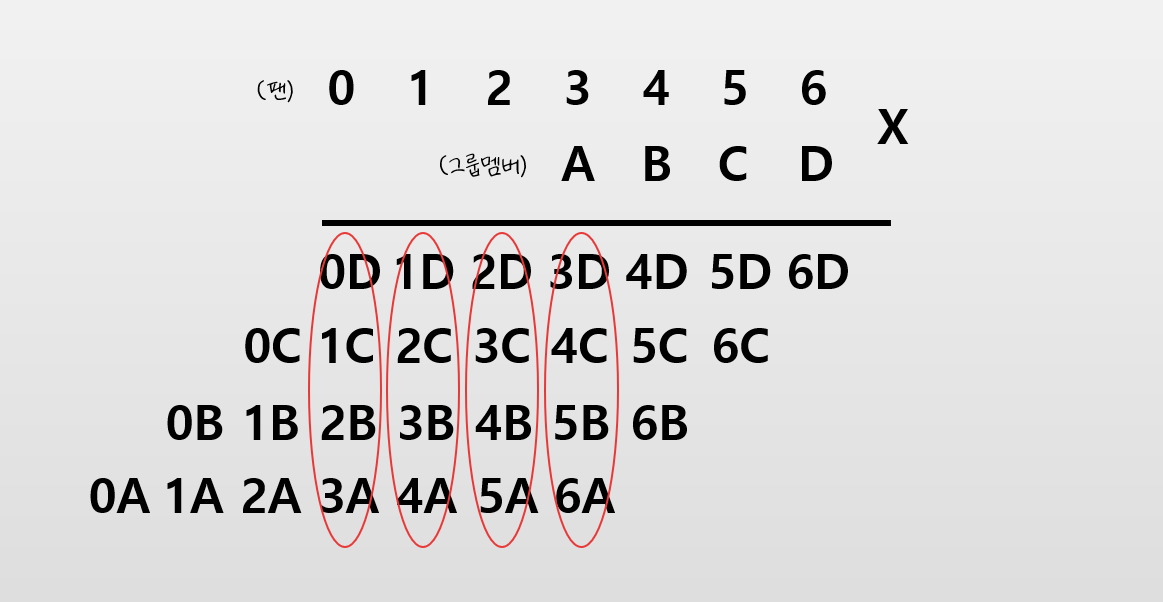
곱한다는 개념을 서로 만난다는 개념으로 치환해서 생각하면 이 문제는 곱셈과정을 이용해서도 구하고자 하는 답을 찾을 수 있다.
예를 들어 입력으로 주어진 팬과 그룹멤버를 곱해본다고 했을 때 그 과정을 한번 떠올려보면, 위 그림과 같이 각 자리계산에 빨간색 원으로 표시된 부분이 존재하는 것을 알 수 있다. 그리고 이 표시된 부분의 팬과 그룹멤버가 이루고 있는 조합이 우리가 구하고자하는 조건과 일치하고 있다는 것을 볼 수 있다. 즉 주어진 팬들과 그룹멤버를 정해진 순서에 따라 1:1로 대응시킬 수 있는 모든 경우의 수가 한번의 곱셈과정 안에 모두 포함되어있어 있고 답을 구할 때는 빨간색 원에 해당하는 부분만 잘 가져와 계산해주면 된다는 것이다.
물론 이렇게 되면 A,B,C,D의 위치가 역전된 상태로 팬들과 만나는 경우가 되는데 이 문제점은 그룹멤버 A,B,C,D를 처음부터 역전시켜 계산시켜주게 되면 간단하게 해결된다.
하지만 여기서 생각해야할 점은 곱하는 과정에서의 시간복잡도이다. 각각 N 개와 N'개의 길이를 가진 두 수의 곱셈과정을 구현했을 때 단순하게 이중 포문으로 각 요소를 곱해주는 것 만으로는 O(N * N')의 시간복잡도를 소모하게된다. 이래서는 원래 생각했던 완전탐색 로직보다도 더 느려진다.
이 때 분할정할을 이용하여 계산 과정을 최적화한 카라츠바의 곱셈 알고리즘을 이용하면 두 수의 곱셈 과정을 기존의 O(N^2)보다 빠른 O(N^log3)의 시간복잡도로 해결할 수 있게 된다. (N == N' 일때)
카라츠바의 빠른곱셈 알고리즘
아주 간단하게 카라츠바 알고리즘에 대해서 설명을 써놓자면 N자리 길이의 두 수 A와 B의 곱을 진행하기 전에
A = (A' * 10^n/2) + A''
B = (B' * 10^n/2) + B''
A * B = (A' * B') * 10^n + [(A' * B'') + (A'' * B')] * 10^n/2 + (A'' * B'')
위와 같이 곱해야할 두 수를 절반의 길이로 나누어 구분시킨 뒤 곱셈을 진행하여, N 길이의 두 수의 곱이 아닌 N/2 길이의 두 수의 곱으로 계산을 진행하도록 하게한다. 즉 두 수의 길이를 계속 절반으로 잘라내어 계산하는 분할정복 패러다임을 이용한 방법. 하지만 이 방법으로 답을 구하기 위해서는 곱해야할 수의 길이가 절반으로 줄어들긴 했어도 대신 총 4번의 곱셈 계산이 필요하게 되므로, 결국 시간복잡도는 O(N^2)으로 수렴하게 된다.
( T(N) = 4 * T(2/N)은 마스터정리로 계산해봤을 때 O(N^2)의 시간복잡도를 가진다는 것을 알 수 있음)
따라서 계산과정에서 도출되는 값들을 적절히 이용하여 처리해야 할 부분문제를 3개로 줄이고 결론적으로 O(3^logN)의 시간복잡도로 두 수의 곱을 계산할 수 있게만든 것이 카라츠바의 빠른곱셈 알고리즘이다.

#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
void addTo(vector<int>& a, vector<int>& b, int b_m) {
for (int i = 0; i < b_m; i++) b.push_back(0);
int fit = a.size() - b.size();
if (fit < 0) {
fit *= -1;
vector<int> temp_a = b;
for (int i = 0; i < a.size(); i++) temp_a[i + fit] += a[i];
a = temp_a;
}
else {
for (int i = 0; i < b.size(); i++) {
a[i + fit] += b[i];
}
}
}
void subFrom(vector<int>& a, vector<int>& b) {
int fit = a.size() - b.size();
if (fit < 0) {
fit *= -1;
vector<int> temp_a = b;
for (int i = 0; i < a.size(); i++) temp_a[i + fit] -= a[i];
a = temp_a;
}
else {
for (int i = 0; i < b.size(); i++) {
a[i + fit] -= b[i];
}
}
}
vector<int> karatsuba(vector<int>& a, vector<int>& b) {
if (a.size() == 0 || b.size() == 0) return vector<int>();
if (a.size() < b.size()) return karatuba(b, a);
if (b.size() == 1) {
if (b[0] == 0) return vector<int>();
else {
vector<int> temp_a(a);
for (int i = 0; i < b.size(); i++) {
temp_a[i] *= b[0];
}
return temp_a;
}
}
int half = a.size() / 2;;
int expoA = a.size() - half;
vector<int> a0(a.begin(), a.begin() + half);
vector<int> a1(a.begin() + half, a.end());
vector<int> b0, b1;
int expoB = b.size() - expoA;
if (expoB <= 0) b1 = b;
else {
vector<int> temp_b0(b.begin(), b.begin() + expoB);
vector<int> temp_b1(b.begin() + expoB, b.end());
b0 = temp_b0;
b1 = temp_b1;
}
vector<int> z0 = karatsuba(a0, b0);
vector<int> z1 = karatsuba(a1, b1);
addTo(a0, a1, 0);
addTo(b0, b1, 0);
vector<int> z2 = karatsuba(a0, b0);
subFrom(z2, z0);
subFrom(z2, z1);
vector<int> ret;
addTo(ret, z1, 0);
addTo(ret, z2, expoA);
addTo(ret, z0, expoA * 2);
return ret;
}
int fanmeeting(vector<int>& group, vector<int>& fan) {
int count = 0;
int chance = fan.size() - group.size() + 1;
if (chance <= 0) return count;
vector<int> ret = karatsuba(group, fan);
int remove = ret.size() - (fan.size() + group.size() - 1);
for (int i = 0 + remove; i < chance + remove; i++) {
if (ret[group.size() - 1 + i] == 0) count++;
}
return count;
}
int main() {
int testcase;
scanf("%d", &testcase);
getchar();
for (int i = 0; i < testcase; i++) {
vector<int> group;
vector<int> fan;
char temp;
while (true) {
scanf("%c", &temp);
if (temp == '\n') break;
if (temp == 'F') {
group.push_back(0);
}
else group.push_back(1);
}
while (true) {
scanf("%c", &temp);
if (temp == '\n') break;
if (temp == 'F') {
fan.push_back(0);
}
else fan.push_back(1);
}
reverse(group.begin(), group.end());
int ret = fanmeeting(group, fan);
printf("%d\n", ret);
}
return 0;
}대충 흐름만 확인하고 혼자서 새로 코드를 짜봤지만 시간초과가 뜬 코드. 책과의 차이를 찾아보니 카라츠바 알고리즘은 수를 배열에 저장할 때 뒤에서부터 저장하는 기법을 이용함. 내 코드의 경우는 있는 그대로 앞에서부터 저장하기 때문에 분할되는 수들의 지수계산을 따로 해줘야 하는 등 분할과정이 쉽지 않았다. 확실히 뒤에서부터 저장하는 것이 반으로 분할하는 것도 쉽고 addTo 같은 지수를 따로 더해줘야하는 함수에서도 구현이 편해진다는 걸 느낌. 다른 사람들의 addTo, SubFrom 함수 구현도 한번 찾아봤는데 어쩜 그리도 깔끔하게 코드를 짜는지 내 코드는 보여주기 민망한 수준이더라. 책의 방식대로 다시 한번 짜볼까 하다가 엿같아서 때려침. 대체 어느 부분에서 시간초과가 나는 지는 미스테리로 남았다.
