(출처) https://www.algospot.com/judge/problem/read/FENCE
완전탐색의 경우
입력으로 주어진 울타리 N개가 있을때 0번 울타리부터 N번 울타리까지 모든 울타리를 한 번씩 기준 울타리로 삼아 기준이 되는 자신보다 높이가 작은 울타리가 나오기 전까지 주변 울타리를 탐색하고 탐색이 진행된 횟수에 자신의 높이를 곱하여 저장한다. 만약 모든 울타리의 높이가 동일하게 주어졌다고 하면 N개의 울타리들은 매번 N번씩 탐색을 진행할 것이기 때문에 시간복잡도는 O(N^2)이 된다. 문제에서 주어질 수 있는 울타리의 최대 개수는 2만 개이므로 O(N^2) 시간복잡도로는 2만 X 2만 = 4억 정도의 계산이 필요하게 된다. 1초라는 시간에 4억 개의 반복계산을 수행하는 것은 시간초과가 예상됨으로 더 빠른 알고리즘의 설계가 필요하다
더 빠른 알고리즘이 필요하다
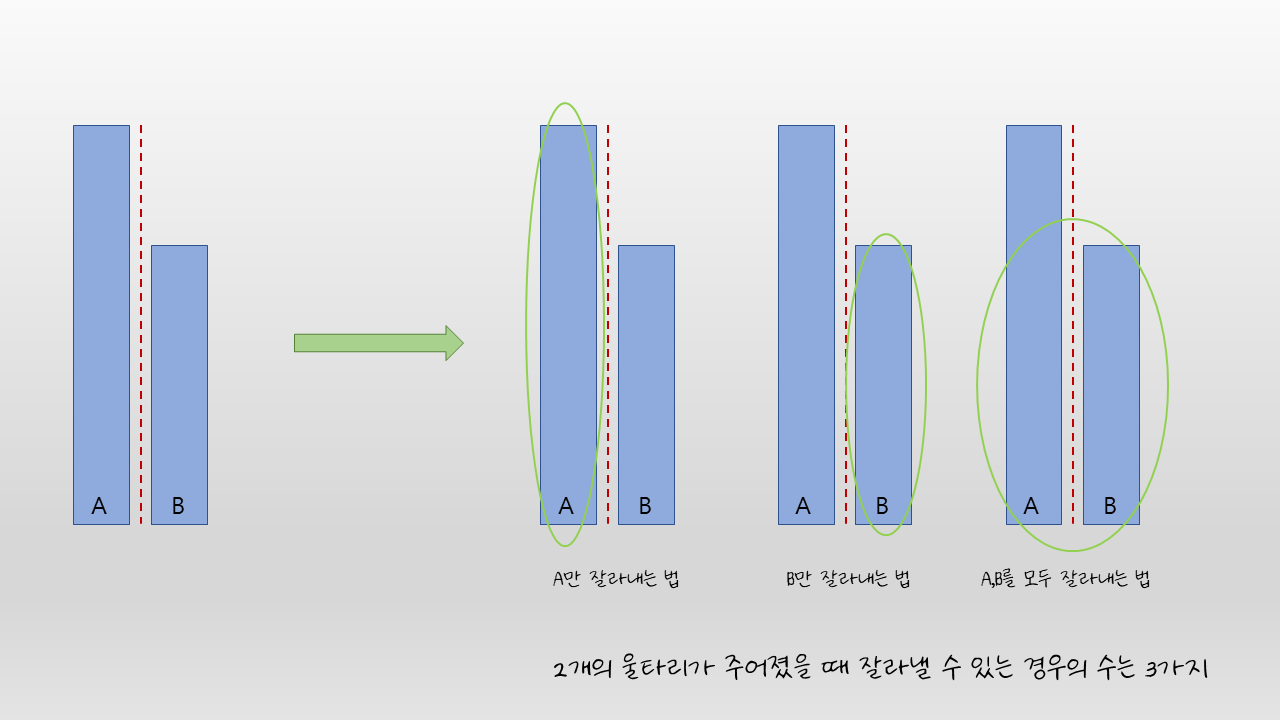
주어진 울타리들의 총 개수가 몇 개인지 상관없이 모든 울타리 집합은 위 그림과 같이 A영역과 B영역을 절반으로 나누어 구분할 수 있다. 그리고 우리가 구하고자 하는 답은 반드시 3가지 경우에 존재한다고 볼 수 있다. 답이 A영역에 존재하는 경우, B영역에 존재하는 경우, A와 B영역에 걸쳐 존재하는 경우. 따라서 각 3가지 경우에서 만들 수 있는 최대값을 각각 구한뒤 가장 큰 값을 뽑으면 올바르게 정답을 구해낼 수 있다.
한 울타리 영역을 절반으로 나누어 나타낸 A와 B영역 역시도 같은 논리로 또 다시 절반으로 나눌 수 있다. 즉 A영역 또한 또다른 A' 와 B' 영역으로 구분되어 질 수 있고 이는 완벽하게 이전 문제의 부분문제로서 재귀적으로 계속 해당 행위를 진행 시킬 수 있다. 이때 기저 사례는 더 이상 절반으로 나눌 수 없이 오로지 단 하나의 울타리만이 영역에 존재할 때 이다.
이때 우리가 구하고자 하는 A만을 잘라내는 경우의 답과 B만을 잘라내는 경우의 답은 결국 재귀적으로 들어간 부분문제가 리턴하는 값이 된다. 즉 한 번의 재귀함수 내에서 해당 2가지 경우를 계산하는데 드는 시간은 이어지는 재귀함수 혹은 부분문제를 푸는 시간에 단순히 종속될 뿐이니, 만약 재귀호출을 제외한 함수의 나머지 부분에서의 수행시간을 O(N)으로 해결할 수만 있다면, 해당 알고리즘의 시간복잡도를 재귀함수의 총 깊이 x N번의 반복으로 결정지을 수 있게된다. 재귀함수의 총 깊이는 울타리 N개를 더 이상 쪼갤 수 없을 때까지 계속하여 절반으로 나눌 수 있는 횟수 = log N(밑: 2) 이므로 결국 해당 문제를 O(N * log N) 으로 풀 수 있다는 것. 결론적으로 O(N) 이하의 시간복잡도로 A,B를 모두 잘라내는 법을 구해낼 수만 있으면 된다.
A와 B를 잘라내는 법
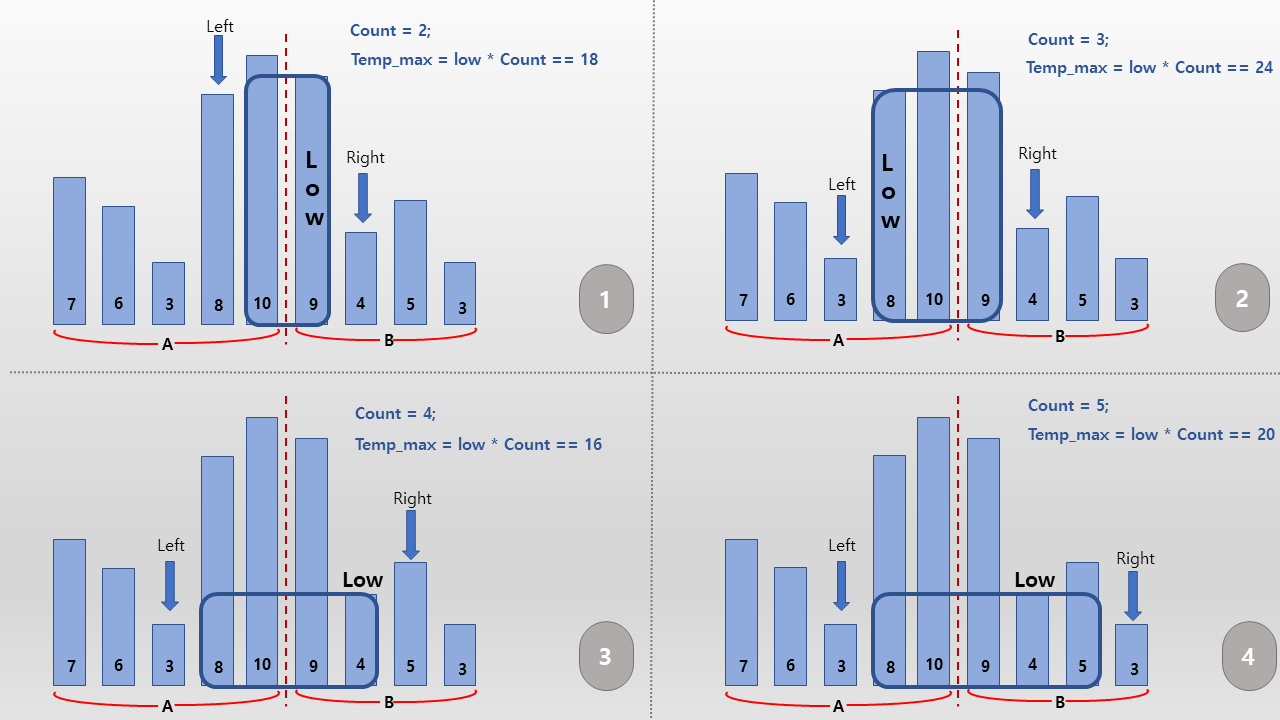
A영역과 B영역을 걸쳐 울타리를 잘라내기 위해선 반드시 A영역의 가장 오른쪽 울타리와 B영역의 가장 왼쪽 울타리를 계산에 포함시켜야 한다. 반드시 포함되어야 하는 2개의 고정울타리를 기점으로 왼쪽 포인터와 오른쪽 포인터를 하나씩 이동시켜가면서 울타리의 영역을 늘려간다. 이때 주의해야 할 점은 영역확장에 있어서 왼쪽과 오른쪽포인터를 고를 때 조건이 존재한다는 점이다. 왼쪽을 먼저 고를지, 오른쪽을 먼저 고를지에 대한 조건이다.
위 그림의 1번 상태에서 2번 상태로 영역을 확장할 때 왼쪽포인터가 가리키는 높이가 8인 울타리와 오른쪽포인터가 가리키는 높이가 4인 울타리 중에, 더 높이가 큰 왼쪽울타리를 선택하고 있는 것을 볼 수 있다. 영역을 확장할 때는 항상 높이가 더 큰 울타리를 우선해서 골라야 한다. 그 이유는 우리가 구하고자 하는 답은 영역 내의 가장 높이가 낮은(LOW) 울타리를 기준으로 영역에 존재하는 울타리의 수(Count)를 곱한 값이므로 만약 2개의 울타리 중에 높이가 더 작은 울타리를 먼저 선택하게 된다면 선택하지 않은 울타리를 Low로 삼는 경우를 완전히 생략해버리게 된다.
즉 위 그림의 2번에서, 높이가 8인 울타리 대신 높이가 4인 울타리를 먼저 선택하여 영역확장을 하게 된다면 Low가 8일때 만들 수 있는 답의 경우를 완전히 생략해 버린다는 것을 알 수 있다. Low는 영역확장을 진행하면서 현재 Low보다 높이가 낮은 울타리로 계속해서 변하기 때문에, 2개의 울타리를 선택할 때 더 높이가 큰 울타리를 우선해서 선택해야지만 가능한 모든 Low 대한 검사를 할 수 있게 된다.
위와 같은 방식으로 존재하는 모든 울타리를 순회한 뒤 가장 높은 Temp_max값을 뽑으면 N번의 순회만으로 A와 B를 잘라내는 방법을 구현할 수 있다.
결론적으로 각 깊이마다 재귀함수는 총 N번의 반복을 수행하고, 해당 문제의 재귀함수의 총 깊이는 log N 개 이므로 전체 시간복잡도가 O(N * logN) 이 되는 알고리즘이 된다.
코드
#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <vector>
#include <algorithm>
using namespace std;
int fence(vector<int> &board, int minNum, int maxNum) {
int left, middle, right;
if (maxNum - minNum == 1) return board[minNum];
if (maxNum - minNum == 2) {
left = board[minNum];
right = board[maxNum - 1];
if (board[minNum] > board[maxNum - 1]) middle = board[maxNum - 1] * 2;
else middle = board[minNum] * 2;
int ret = max(left, right);
return ret = max(ret, middle);
}
int half = (minNum + maxNum) / 2;
left = fence(board, minNum, half);
right = fence(board, half, maxNum);
//middle 구하기
int low;
int count = 2;
if (board[half - 1] <= board[half]) low = board[half - 1];
else low = board[half];
middle = low * count;
int left_p = half - 2;
int right_p = half + 1;
while (left_p >= minNum || right_p < maxNum) {
//예외사항 처리
if (left_p >= minNum && !(right_p < maxNum)) {
if (board[left_p] >= low) {
count++;
middle = max(middle, (low * count));
left_p--;
}
else {
low = board[left_p];
count++;
middle = max(middle, (low * count));
left_p--;
}
}
else if (!(left_p >= minNum) && right_p < maxNum) {
if (board[right_p] >= low) {
count++;
middle = max(middle, (low * count));
right_p++;
}
else {
low = board[right_p];
count++;
middle = max(middle, (low * count));
right_p++;;
}
}
//왼쪽과 오른쪽 어느쪽 선택할지 결정
else {
if (board[left_p] >= board[right_p]) {
if (board[left_p] >= low) {
count++;
middle = max(middle, (low * count));
left_p--;
}
else {
low = board[left_p];
count++;
middle = max(middle, (low * count));
left_p--;
}
}
else {
if (board[right_p] >= low) {
count++;
middle = max(middle, (low * count));
right_p++;
}
else {
low = board[right_p];
count++;
middle = max(middle, (low * count));
right_p++;
}
}
}
}
int ret = max(left, right);
return ret = max(ret, middle);
}
int main() {
int testcase;
scanf("%d", &testcase);
getchar();
for (int i = 0; i < testcase; i++) {
int n;
scanf("%d", &n);
vector<int> board(n);
int temp_int;
scanf("%d", &temp_int);
board[0] = temp_int;
for (int i = 1; i < n; i++) {
scanf("%d", &temp_int);
board[i] = temp_int;
}
int ret = fence(board, 0, n);
printf("%d\n", ret);
}
return 0;
}기억하고 싶은 점
내가 짠 코드는 if 조건을 무분별하게 사용해서 쓸데없이 동일한 코드가 중복되고 길어지는 면이 있었는데 책의 코드를 보고 깔끔하게 if 조건문 하나로 모든 경우를 완벽히 제어하는 것을 보고 놀랐다. 특히 if (A && (B || C) 와 같은 방식으로 조건문을 짜는 것은 기억해두고 싶었다.
또한 배열의 인덱스를 다룰 때 인덱스 계산에 쓸데없이 시간을 많이 소요하게 되는 경우가 많은데 그냥 반열림 구간을 이용해서 생각을 추상화하는 것이 실수도 줄이고 쓸데없는 계산에 생각을 자꾸 할애하는 것을 줄일 수 있다는 것을 느낌.
벡터를 넘길 때 포인터를 이용하지 않고 벡터 그 자체를 넘겨서 함수 내에서 계속 벡터를 생성하게 되어 시간초과가 떴는데 이걸 찾아내려고 꽤나 시간이 소모됐다. 앞으로 커다란 데이터를 넘길 땐 한 번씩 주의해야겠다.
