(출처) https://algospot.com/judge/problem/read/FORTRESS
가장 벽을 많이 넘어야하는 두 지점
하나의 성이 다른 성들을 포함할 수 있으며 성끼리 서로 겹치거나 닿을 수 없다는 조건은 입력으로 주어지는 성들을 트리로 구현하라고 대놓고 유도하는 것 같았다.
문제가 요구하는 것은 여러개의 성이 주어졌을 때 가장 벽을 많이 넘어야 하는 두 지점을 찾아내는 것이다.
나는 먼저 주어지는 성들을 트리로 구현하고 트리를 순회하며 각각의 트리객체에 높이를 저장한 뒤 해당 높이를 이용하여 답을 구해낼 방법이 없는 지 생각해보았다.
각 트리노드의 높이를 구해 따로 저장해주는 것은, 가장 바닥의 높이가 0인 잎노드부터 부모노드를 거슬러 올라가 방문하면서 기존의 높이에 1을 추가해주고 저장하는 식으로 모든 노드를 1번씩 순회하면 된다. 이 과정은 O(N)의 시간복잡도로 수행이 가능하다.
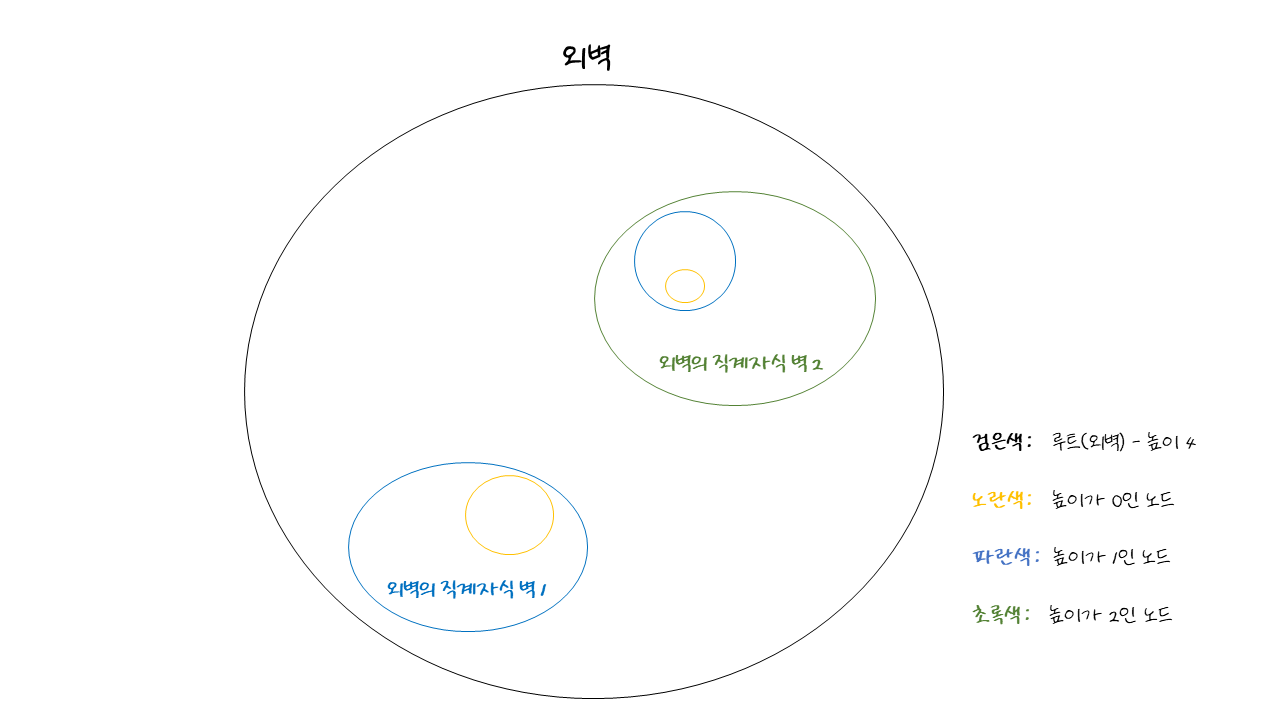
외벽을 기준으로 해당 성안에서 가장 벽을 많이 넘어야 하는 두 지점이 과연 몇 개의 벽을 넘는지 세어 본다고 하면, 직관적으로는 외벽의 직계자손들끼리 높이를 더하는 것이 가장 최적해 같아 보인다.
외벽의 직계자손들의 높이는 해당 성 안쪽 가장 깊은 곳에 있는 성부터 성을 넘기 시작했을 때의 값이라고도 볼 수 있으므로 각 직계자손들끼리 쌍을 지어 서로의 높이를 합하면 답을 구할 수 있지 않을까 생각했다.
(정확하게는 두 직계자손들의 높이 합에 2를 더해주는 것이 올바른 최대성벽넘기의 답이지만, 구체적인 부분까지 생각하면서 모든 로직을 설계하는 건 비효율적이니 일단 세세한 계산식은 생략하고 높이를 이용해 답을 구하는 방식을 찾는데만 초점을 맞췄다)
따라서 루트의 높이(외벽의 높이)를 초기 ret으로 두고 슬하의 모든 자식들을 두 쌍씩 짝지어 높이 합을 구해줬을 때 가장 큰 Max 값을 리턴해주는 식으로 코드를 구현했다.
ret = max(ret, 루트의 직계자손들 중 두 쌍의 높이 합)이때 최초의 ret은 root의 높이가 들어가며, 모든 직계자손 두 쌍의 경우를 전부 확인할 때 까지 ret 갱신을 반복한다
루트의 직계자손을 두 쌍씩 모두 짝지어 주기 위해서는, 모든 자식후보 최대 n 개를 자신과 짝이 될 자식후보 n-1 개와 결합시켜줘야 하므로 총 (n * (n -1) / 2) 번의 계산이 필요하다. 따라서 해당 과정은 최대 O(N^2)의 시간복잡도가 소모된다.
하지만 이 방식에는 허점이 존재하는데,
바로 외벽의 직계자식 안에서 최대성벽넘기의 답이 존재하는 경우이다.
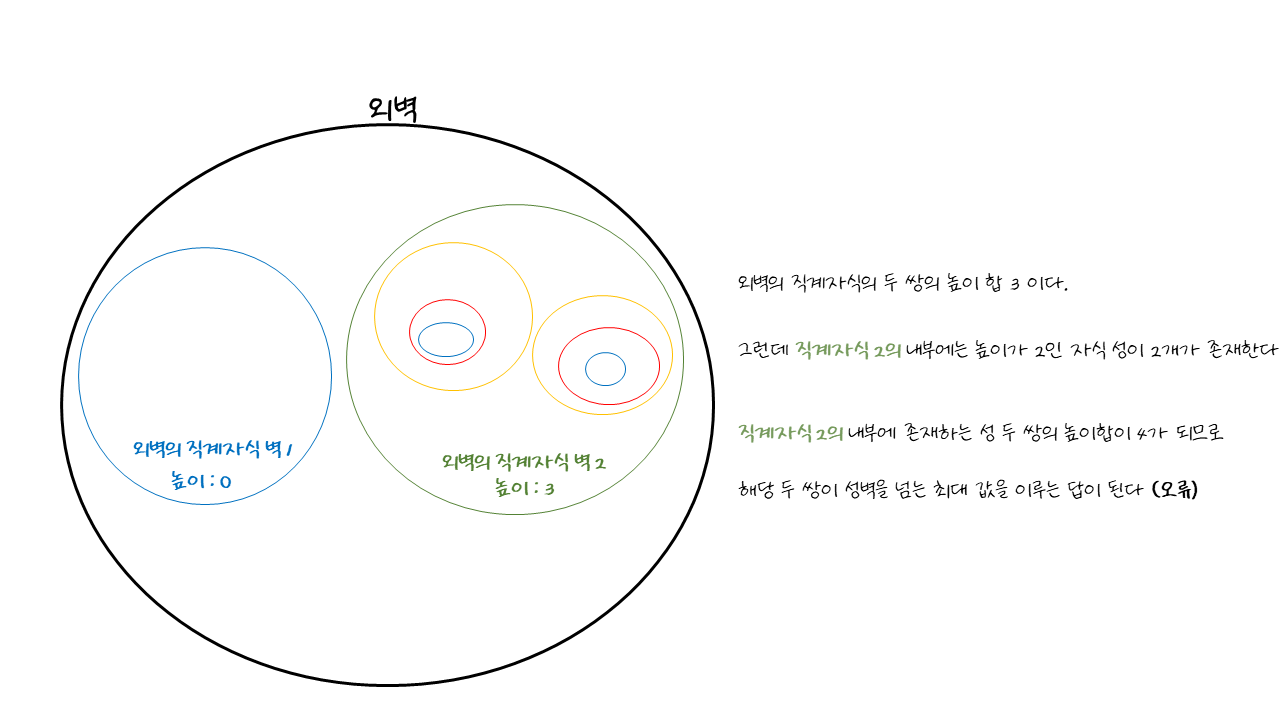
따라서 외벽 직계자손들끼리의 두 쌍 높이합 뿐만이 아니라, 직계자손 내부에서도 최대 값을 이루는 두 쌍의 성이 존재하는 지 확인을 해주어야 하므로, 각 직계자손 내부에서도 최대벽넘기 구하기 과정을 돌려주어야한다. 이것은 외벽 슬하의 모든 직계자손들을 또 다른 외벽루트라고 생각하고 해당 성 안에서 최대벽넘기 구하기 과정을 재귀적으로 반복해 주면 된다.
기존의 최대벽넘기 로직은 총 O(N^2)의 시간복잡도을 필요로 하는데, 최대 N 개의 자식마다 최대벽넘기를 찾는 과정을 다시 반복해 주어야 하므로 최종 시간복잡도는 O(N^3)이 된다.
이때 입력으로 올 수 있는 N의 최대값은 100이므로 O(N^3)은 충분히 해결할 수 있는 선이다.
트리의 구현
입력으로 주어지는 첫 번째 성벽은 root이다. 따라서 첫 번째 입력을 root로 하여 트리를 최초로 생성한다. 이후 입력으로 들어올 노드 N-1 개는, 현재까지 만들어놓은 트리를 하나씩 순회시키면서 대상입력노드가 트리의 어느 위치에 들어가야하는 지 판단해주어 적절한 위치에 삽입시켜주면 된다.
이때 입력노드를 삽입시킬 적절한 위치를 찾는 과정은 현재까지 만들어놓은 트리 중 루트의 직계자식들부터 시작해, 나머지 모든 노드를 모두 방문하면서 진행된다. 트리를 순회하면서 입력노드와 방문한 노드의 포함관계를 확인하는 것.
만약 모든 루트의 직계자식들과 입력노드의 포함관계가 발견되지 않았다면 해당 입력노드는 루트의 새로운 직계자손이 될 것이다.
반대로 포함관계가 확인되었을 경우엔 다시 2가지 경우로 세분된다.
입력노드가 대상이 된 루트의 직계자식을 포함하고 있는 경우와 역으로 루트의 직계자식이 입력노드를 포함하고 있는 경우이다.
전자의 경우에는 기존루트의 직계자식이 입력노드의 자식으로 들어가고 입력노드가 루트의 새로운 직계자손으로 바뀌게 되면서 삽입은 종료된다.
후자의 경우는 루트의 직계자식 내부로 탐색을 이어나가야 하기 때문에, 현재 대상이 된 루트의 직계자식이 새로운 루트가 되어 다시 위의 과정을 입력노드의 삽입이 종료될 때까지 재귀적으로 계속 반복해야 한다.
결국 입력노드는 최대 N 개의 노드를 순회하며 삽입될 위치가 결정되므로, 노드를 삽입시키위해 적절한 위치를 찾는 과정은 최대 O(N)의 시간복잡도가 들게 된다. 삽입될 위치를 적절하게 찾기만 한다면 노드를 삽입하는 것 자체는 노드의 부모와 자식을 가리키는 포인터만 새롭게 변경해주면 되므로 O(1) 상수시간에 해결이 가능하다.
따라서 트리를 만드는 과정은 총 n-1개의 입력노드들이 각 최대 n번 씩의 탐색을 진행해야하므로 (n-1) * n == O(N^2)의 시간복잡도를 필요로 한다.
코드
#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <algorithm>
#include <vector>
using namespace std;
struct tree {
int height;
int x, y, r;
tree* parent;
vector<tree*> children;
int get_height(tree* root) {
int h = 0;
for (int i = 0; i < root->children.size(); i++) {
h = max(h, 1 + get_height(root->children[i]));
}
root->height = h;
return h;
}
};
int sqr(int x) {
return x * x;
}
//포함관계가 없을 때 0, node1 > node2 일때 1, node1 < node2 일때 2
int judge_relation(tree* node1, tree* node2) {
int dist = sqr(node1->x - node2->x) + sqr(node1->y - node2->y);
if (node1->r > node2->r && dist < sqr(node1->r - node2->r)) return 1;
else if (node1->r < node2->r && dist < sqr(node1->r - node2->r)) return 2;
else return 0;
}
void makingTree(tree* root, tree* node) {
for (int i = 0; i < root->children.size(); i++) {
int judge = judge_relation(node, root->children[i]);
if (judge) {
if (judge == 1) {
node->children.push_back(root->children[i]);
node->parent = root;
root->children[i]->parent = node;
root->children[i] = node;
return;
}
else if (judge == 2) {
makingTree(root->children[i], node);
return;
}
}
}
int judge = judge_relation(root, node);
if (judge) {
root->children.push_back(node);
node->parent = root;
}
}
int fortress(tree* root, int ret) {
// O(N^2)
for (int a = 0; a < root->children.size(); a++) {
for (int b = a + 1; b < root->children.size(); b++) {
ret = max(ret, root->children[a]->height + root->children[b]->height + 2);
}
}
// O(N^3)
for (int i = 0; i < root->children.size(); i++) {
ret = max(ret, fortress(root->children[i], ret));
}
return ret;
}
int main() {
ios::sync_with_stdio(false);
cin.tie(NULL);
cout.tie(NULL);
int testcase;
cin >> testcase;
while (testcase--) {
int n;
cin >> n;
vector<int> temps;
temps.reserve(3);
for (int i = 0; i < 3; i++) {
int temp;
cin >> temp;
temps.push_back(temp);
}
// 주어진 입력으로 트리 만들기 O(N^2)
tree root{ 0, temps[0], temps[1], temps[2] };
for (int i = 0; i < n - 1; i++) {
temps.clear();
for (int i = 0; i < 3; i++) {
int temp;
cin >> temp;
temps.push_back(temp);
}
tree* node = new tree{ 0, temps[0], temps[1], temps[2] };
makingTree(&root, node);
}
//각 노드의 height 구하기 O(N)
root.get_height(&root);
int ret = fortress(&root, root.height);
cout << ret << "\n";
cout << "hi";
}
return 0;
}기억하고 싶은 점
나는 트리의 루트만을 스택에 저장하고 나머지 루트의 자손들은 new 연산자를 통해 힙메모리에 동적할당하였다.
그런데 동적으로 할당되는 자손노드들은 지역함수 내 하나의 포인터만을 이용해서 컨트롤을 하고 있기 때문에, 대상이 된 노드가 한번 트리에 저장이 되고 나서 대상에서 벗어나 버리게되면 더 이상 이 노드를 참조할 방법이 존재하지 않았다.
오로지 루트노드에서부터 자식노드들을 따라가며 하나하나씩 방문하여 참조해주는 수밖에 없었다.
그래서 이 동적으로 할당한 트리 객체들을 후에 다시 삭제해 주는 게 무척이나 귀찮았다.
물론 하나씩 순회를 하며 하나씩 메모리에서 해제해 주면 되긴 하겠지만 막상 정답을 띄우고 최적화를 위해 다시 구현하자고 하니 귀찮아지더라.
해당 문제는 테스트케이스 횟수와 입력으로 주어지는 노드가 적어서 딱히 메모리를 해제해 주지 않아도 정답을 띄울 수 있었지만 나중에는 분명 이런 부분에서 한 번쯤은 문제가 될 것 같긴 했다. 이 점은 기억해 두고 싶었다.
또한 트리의 최대 경로를 찾는 책의 해답도 알아두면 좋을 것 같았다. 트리의 최대 경로 찾기는 앞으로도 많이 왠지 많이 써먹을 것 같은 느낌이 들어서 유심히 보는게 좋을 것 같다.
그리고 책에서는 높이합이 최대가 되는 두 쌍을 찾기 위해서 나처럼 2중 for문을 돌리지않고, 단순하게 모든 성의 높이들을 정렬시킨 뒤 마지막 두 원소를 꺼낸다.
따라서 총 n개의 노드순회마다 O(N x lg N)의 시간복잡도를 정렬하는데 사용하므로, 전체 시간복잡도는 O(N^2 x lg N)이 된다.
나의 알고리즘의 경우 높이합이 최대가 되는 두 쌍을 찾는 것에 O(N x lg N) 이 아닌 O(N^2)을 소요했으므로, 전체 시간복잡도는 O(N^3) 이었다. 정렬이라는 아이디어는 기억하고 싶다.
마지막 여담으로 트리 구현을 처음 해보다 보니까 구현하는데 시간이 꽤나 오래 걸렸는데 이렇게 자료구조를 직접 구현해가며 문제 푸는 것도 충분히 좋은 경험이었다고 생각한다.
