TRAVERSAL(트리순회변경)

(출처) https://algospot.com/judge/problem/read/TRAVERSAL

2가지 정보에서 새로운 정보를 추출해내기

해당 문제에서 주어지는 트리는 이진트리의 특성을 가지고 있다. 따라서 트리에 속하는 그 어떤 노드를 바라보더라도 해당 노드를 루트로 하고 2개의 서브트리를 가지고 있는 또 다른 트리로 구분시킬 수가 있다. 이 점을 활용하여 계속 재귀적으로 반복한다면 문제의 답을 충분히 구해낼 수 있지 않을까라는 생각을 했다.

전위순회에서 가장 처음으로 오는 수가 바로 트리의 루트이므로, 전위순회의 가장 첫 번째 수를 기준으로 탐색을 진행하기로 한다.

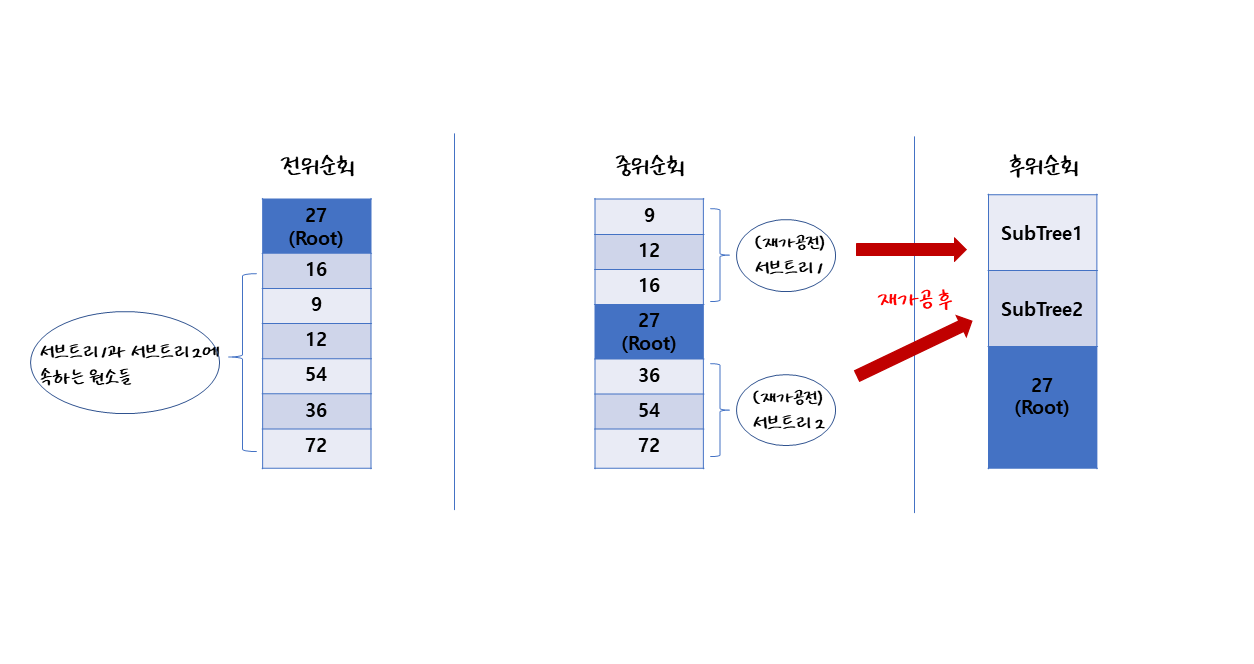
그런데 전위순회에서 기준이 되는 루트는 찾았어도, 루트에서 2개의 서브트리가 어떻게 쪼개지게 되는지에 대한 판단을 내리기에는 정보가 부족하다. 따라서 중위순회의 정보를 이용해야 한다. 중위순회에서 기준루트를 기준으로 자신보다 먼저 들어온 수들은 서브트리1이 될 것이고, 자신 이후에 등장하는 수들은 서브트리2가 될 것이다.

이렇게 되면 후위순회의 순서도를 구할 때 필요한 정보의 조각은 모두 다 얻어냈다. 이 정보를 재가공한 뒤 후위순회의 순서도를 서브트리1, 서브트리2, 루트 순으로 정렬시키면 원하는 답을 구해낼 수 있다. 서브트리1, 서브트리2를 재가공하여 순서도를 얻는 과정도 방금까지의 과정을 재귀적으로 계속 반복해서 구할 수 있다. 마지막에 재가공된 모든 조각을 다 합쳐주기만 하면 된다.

시간복잡도

전위순회의 모든 노드가 1번씩은 기준점이 되어야 하기 때문에 전체 재귀함수의 반복은 N번이 된다. 그리고 각 1번의 반복마다 기준점이 되는 노드가(루트) 중위순회에 어느 위치에 존재하는지 검사를 하면서 N 번의 반복을 수행해야 한다. 따라서 시간복잡도는 N * N 인 O(N^2)이 된다.

코드

#define _CRT_SECURE_NO_WARNINGS
#include <iostream>
#include <algorithm>
#include <list>
#include <string>

 using namespace std;
 int n;

 //preorder을 기준으로 sub1, sub2, sub3로 나눠서 해결한다. inorder은 sub1, sub2, sub3의 구획을 어떻게 나눠야하는지에 대한 정보를 제공한다. 
 string traversal(list<int> &preorder, list<int>& inorder) {
	 //기저사례
	 if (preorder.size() == 0) return "";
	 string root = to_string(preorder.front());;
	 if (preorder.size() == 1) return root;
	 //중위순회 배열에서 root 원소의 인덱스를 찾는다
	 auto root_inorder = inorder.begin();
	 for (int i = 0; i < inorder.size();i++) {
		 if (*root_inorder == preorder.front()) break;
		 root_inorder++;
	 }

	 //inorder part
	 list<int> sub2_inorder;
	 sub2_inorder.splice(sub2_inorder.begin(), inorder, root_inorder, inorder.end());
	 sub2_inorder.erase(sub2_inorder.begin());
	 //preorder part
	 list<int> sub2_preorder;
	 auto root_preorder = preorder.begin();
	 for (int i = 0; i < inorder.size() + 1; i++) root_preorder++;
	 sub2_preorder.splice(sub2_preorder.begin(), preorder, root_preorder, preorder.end());
	 preorder.erase(preorder.begin());

	 string sub1 = traversal(preorder, inorder);
	 string sub2 = traversal(sub2_preorder, sub2_inorder);
	 string sub3 = root;

	 string * temp[3] = { &sub1, &sub2, &sub3 };
	 for (int i = 0; i < 3; i++) {
		 if ( (*temp[i]).size() >= 1) *temp[i] = *temp[i] + " ";
	 }
	 string ret = sub1 + sub2 + sub3;
	 if (ret.back() == ' ') ret.pop_back();

	 return ret;
}


int main() {
	ios::sync_with_stdio(false);
	cin.tie(NULL);
	cout.tie(NULL);

	int testcase;
	cin >> testcase;
	while (testcase--) {
		cin >> n;
		list<int> preorder;
		list<int> inorder;
		int temp;
		for (int i = 0; i < n; i++) {
			cin >> temp;
			preorder.push_back(temp);
		}
		for (int i = 0; i < n; i++) {
			cin >> temp;
			inorder.push_back(temp);
		}
		string ret = traversal(preorder, inorder);
		cout << ret << "\n";
	}
	return 0;
}

기억하고 싶은 점

이 문제의 알고리즘은 전위순회, 중위순회의 순회표를 알맞게 잘라내어 다시 재귀를 반복하는 식으로 진행한다. 나는 연결리스트를 이용해 전위,중위 순회표를 저장하였고 연결리스트의 splice 메서드로 특정 위치로 부터 원소를 잘라내어 또 다른 연결리스트에 저장하는 식으로 구현을 하였다.

하지만 책에 구현은 그냥 vector에 순회표를 저장하고 따로 slice 함수를 구현해서 진행하더라.

굳이 비교하자면 생소한 연결리스트를 이용하는 것보다 벡터를 이용하는 책의 구현이 더 나았던 것 같다. 이런식의 구현도 기억해 두고 싶다.