Deep Learning - 딥러닝 이론 정리 1 (퍼셉트론 구조, 연산, 가중치와 편향, 활성화 함수)

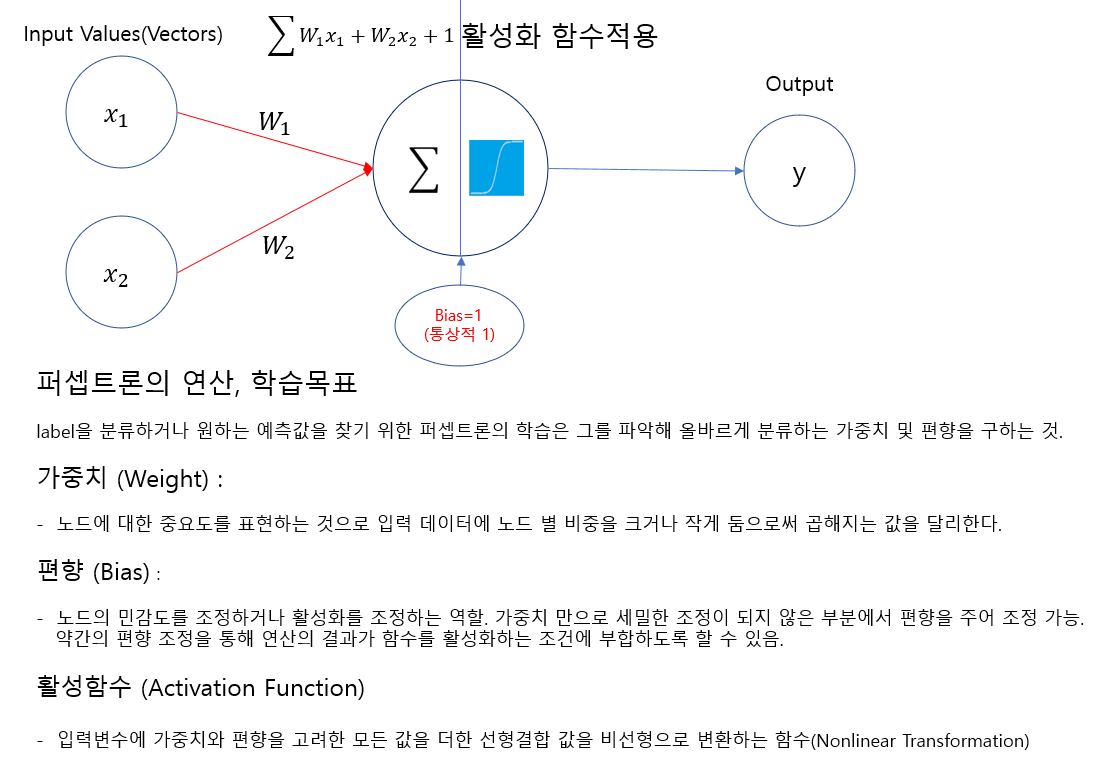
퍼셉트론(Perceptron)

신경망을 이루는 가장 기본이 되는 단위 - 여러개의 입력을 받아 하나의 출력을 하는 신경세포 뉴런과 유사

퍼셉트론의 구조

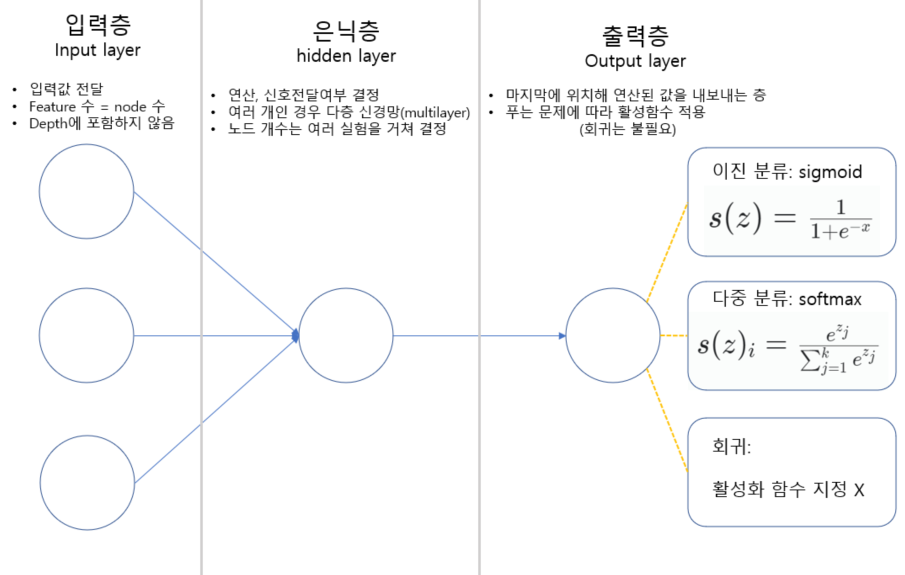
입력층 (Input Layer)

• 입력값을 전달하는 층
• 입력 Feature 수에 따라 node 수가 결정된다.
• Depth 파악 시 포함하지 않는다.

은닉층 (Hidden Layer)

• 입력받은 데이터를 가중치와 편향에 따라 연산하는 층
• 여러 개인 경우 다층 신경망(MultiLayer)
• 노드 개수를 정하는 명확한 기준은 없다. 해당 엔지니어의 실험에 따라 원하는 만큼 결정가능

출력층 (Output Layer)

• 마지막 Layer에 위치해 연산된 값을 내보내는 층
• 푸는 문제에 따라 활성함수 적용 (일반적으로 회귀문제에는 적용하지 않음)

퍼셉트론의 연산, 학습목표

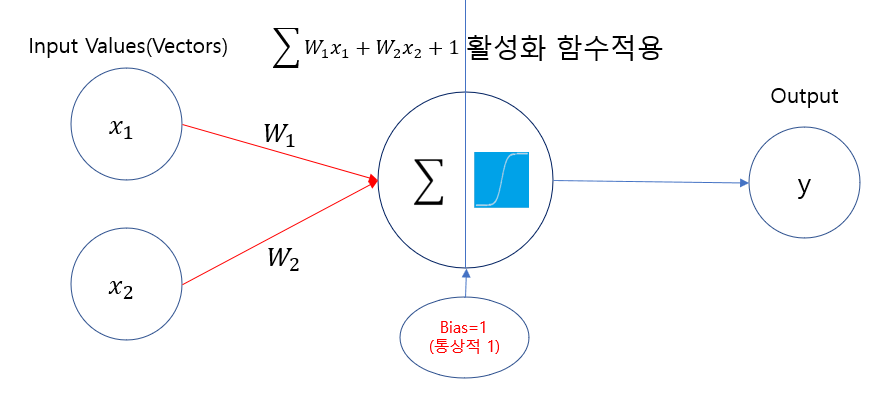
label을 분류하거나 원하는 예측값을 찾기 위한 퍼셉트론의 학습은 그를 파악해 올바르게 분류하는 가중치 및 편향을 구하는 것.

퍼셉트론의 기본 연산 구조를 수식으로 표현하면 아래와 같다.
$y = f(\sum W_ix_i +b$)
$= f[\sum(b+W_0x_0+W_1x_1+...+W_ix_i]$

• 입력값을 전달받음
• 입력값에 가중치를 곱한 뒤, 편향을 더해 선형결합을 진행
• 활성함수를 통해 비선형으로 변환
• 역전파 알고리즘을 통해 오차가 최소화 되도록 하는 가중치 및 편향 확인 > 미분 & 경사하강법

가중치 (Weight) $W$

노드에 대한 중요도를 표현하는 것으로 입력 데이터에 노드 별 비중을 크거나 작게 둠으로써 곱해지는 값을 달리한다.

일반적으로 W로 표기하며, 해당 layer에서의 일종의 흐름을 만드는 필터 역할을 한다.

편향 (Bias) $b$

노드의 민감도를 조정하거나 활성화를 조정하는 역할을 한다. 가중치 만으로 세밀한 조정이 되지 않은 부분에서 편향을 주어 조정이 가능하다.

경우에 따라 활성화를 조정할 때에도 사용이 된다. 약간의 편향 조정을 통해 연산의 결과가 함수를 활성화하는 조건에 부합하도록 만드는 방법.

활성화 함수 (Activation Function)

입력변수에 가중치와 편향을 고려한 모든 값을 더한 선형결합 값을 비선형으로 변환하는 함수(Nonlinear Transformation)

• 이진분류: sigmoid함수사용 - 0~1까지의 label의 확률을 파악해 예측
  $s(z) = \frac{1}{1+e^{-x}}$

• 다중 분류: softmax함수사용 - 연산한 값을 확률로 확인이 가능하도록 하는 함수. 전체 label 중 특정 label일 확률을 파악하는 방법.
  $s(z)_i = \frac{e^{z_j}}{\sum_{j=1}^ke^{z_j}}$

• 회귀 문제: 일반적으로 활성화 함수를 사용하지 않는다. 예측값을 그대로 사용하면 되기 때문.

• 그 외: ReLU, Leaky ReLU 등 여러 함수를 상황에 맞게 사용가능