Ridge Regression
Rigdge 회귀는 기존 Linear Rigression의 과적합을 해결해주는 굉장히 현실적인 선형회귀방법이다. 너무나 많은 학습으로 인해 과적합되는 상황에서 편향을 조금 더 주어 결과의 분산을 낮추는 방법이다.
우선 Ridge Regression의 수식을 알아보면, 아래와 같다.
:
로 선형회귀식의 목적이었던 target과의 RSS를 최소로하는 비용함수를 그대로 사용하되, 뒤에 라는 녀석이 추가 된 것을 알 수 있다. RSS + 로 보면 된다.
(람다, lambda)란?
- 그 수치가 커지면 회귀식 매개변수의 증가량이 달라진다. 즉 기울기를 조절해 회귀계수를 조정할 수 있는 것이다. 패널티, 규제의 개념
- 0 ~ 까지 나올 수 있으며, 0일 경우 RSS만 최소화 하는 선이 되므로 기존 선형회귀모델과 같게 된다.
- parameter tuning을 통해서 편향과 분산의 균형잡힌 회귀모델을 작성가능하도록 도와준다.
Ridge Regression 모델 작성해보기
시각적 설명과 편의를 위해 데이터는 비교적 쉽게 '공부시간에 따른 점수'를 통해 단순선형회귀 모델을 만들어 보도록 하겠다.
import pandas as pd
# 공부시간에 따른 점수 표
df = pd.DataFrame({'Study time':[3,4,5,8,10,5,8,6,3,6,10,9,7,0,1,2],
'Score':[76,74,74,89,92,75,84,82,73,81,89,88,83,40,70,69]})
import seaborn as sns
# 스캐터플랏으로 관계 확인
sns.scatterplot(data = df, x = 'Study time', y = 'Score');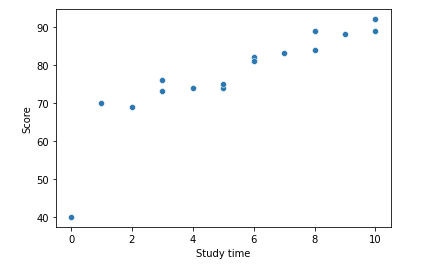
위와 같이 0시간 공부한 것이 0인 것과 같이 하나의 이상치를 넣어서 데이터를 짜봤다.
여기서 train set으로 Linear Regression을 작성해 plot으로 시각화를 해보겠다.
test set과 비교를 해보겠다.
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression
import numpy as np
import matplotlib.pyplot as plt
# train / test data 나누기 test data를 전체 데이터의 50%로 사용
df_train, df_test = train_test_split(df, test_size = 0.5, random_state = 5)
X_train = df_train[['Study time']]
y_train = df_train['Score']
X_test = df_test[['Study time']]
y_test = df_test['Score']
# 단순선형회귀모델 작성
model = LinearRegression()
# 훈련용 데이터로 학습
model.fit(X_train, y_train)
# 테스트용 데이터에 모델적용 예측값 y_pred에 입력
y_pred = model.predict(X_test)
# 기존 전체 data plot
fig, ax = plt.subplots(1,2)
sns.scatterplot(data = df, x = df['Study time'], y = df['Score'], ax = ax[0]);
# 회귀모델 적용 예측값 red로 표현
sns.scatterplot(data = X_test, x = X_test['Study time'],
y = y_pred, color= 'red', ax = ax[0]);
# 회귀선 line으로 표현
sns.scatterplot(data = df, x = df['Study time'], y = df['Score'], ax = ax[1]);
sns.scatterplot(data = X_test, x = X_test['Study time'],
y = df_test['Score'], color = 'orange',ax = ax[1]);
# 회귀모델 적용 예측값 red로 표현
sns.lineplot(data = X_test, x = X_test['Study time'],
y = y_pred, color= 'red', ax = ax[1]); 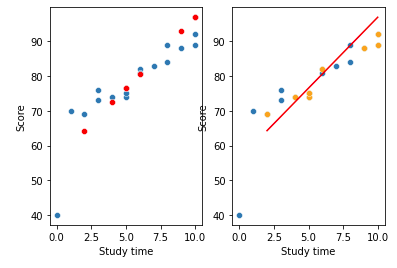
왼쪽의 플랏은 test set의 X에 대한 y를 예측한 값을 red로 표시했고,
오른쪽의 플랏은 회귀선을 긋고 y_test의 실제 값들과의 간격을 보기 위해서 y_test data를 yellow로 표시했다.
사실 나쁘지 않은 회귀선이 만들어져 보일 수 있지만, 우리는 항상 더 나은 성능의 모델이 필요로 된다. Ridge Regression을 사용해서 약간 손을 보도록한다.
from sklearn.linear_model import Ridge
# 단순선형회귀모델 작성
model1 = Ridge()
model1.fit(X_train, y_train)
y_pred1 = model1.predict(X_test)
fig, ax = plt.subplots(1,2)
sns.scatterplot(data = df, x = df['Study time'], y = df['Score'], ax=ax[0])
sns.scatterplot(data = X_test, x = X_test['Study time'], y = df['Score'], color = 'orange',ax = ax[0]);
sns.scatterplot(data = df, x = df['Study time'], y = df['Score'], ax=ax[1])
sns.scatterplot(data = X_test, x = X_test['Study time'], y = df['Score'], color = 'orange',ax = ax[1]);
sns.lineplot(data = X_test, x = X_test['Study time'], y = y_pred1, color = 'red', ax = ax[0]).set_title('RidgeRegression')
sns.lineplot(data = X_test, x = X_test['Study time'], y = y_pred, color= 'red', ax = ax[1]).set_title('LinearRegression')
plt.show();
print('Linear model 회귀계수:', model.coef_[0])
print('Ridge model 회귀계수:', model1.coef_[0])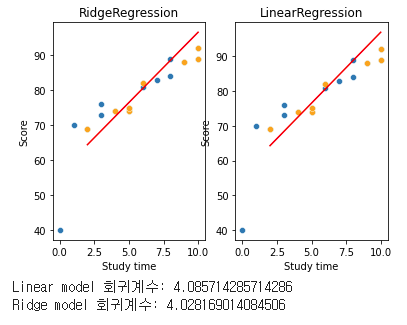
model에 Linear, model1에 Ridge를 적용했는데, 플랏도 크게 다르지 않고, 회귀계수도 큰 변동이 없다. 이는 alpha값(람다, 페널티, 규제)을 설정하지 않아서 그렇다. 한번 여러번 돌려보도록 한다.
from sklearn.linear_model import Ridge
alphas = [0,4,8,12]
def ridgeresearch(df, X_train, y_train, X_test, alpha):
model = LinearRegression()
model.fit(X_train, y_train)
y_pred = model.predict(X_test)
model1 = Ridge(alpha = alpha)
model1.fit(X_train, y_train)
y_pred1 = model1.predict(X_test)
fig, ax = plt.subplots(1,2)
sns.scatterplot(data = df, x = df['Study time'], y = df['Score'], ax=ax[0])
sns.scatterplot(data = X_test, x = X_test['Study time'],
y = df['Score'], color = 'orange',ax = ax[0]);
sns.scatterplot(data = df, x = df['Study time'], y = df['Score'], ax=ax[1])
sns.scatterplot(data = X_test, x = X_test['Study time'],
y = df['Score'], color = 'orange',ax = ax[1]);
sns.lineplot(data = X_test, x = X_test['Study time'], y = y_pred1,
color = 'red', ax = ax[0]).set_title('RidgeRegression')
sns.lineplot(data = X_test, x = X_test['Study time'], y = y_pred,
color= 'red', ax = ax[1]).set_title('LinearRegression')
plt.show();
print('Linear model 회귀계수:', model.coef_[0])
print('Ridge model 회귀계수:', model1.coef_[0])
print('Ridge model 람다값:', model1.alpha)
for i in alphas:
ridgeresearch(df, X_train, y_train, X_test, i)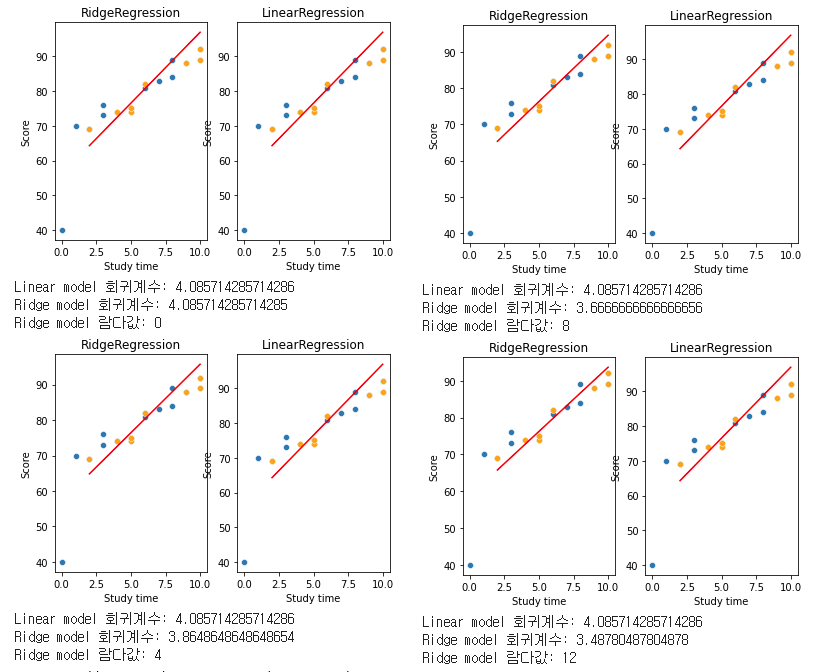
람다값으로 0, 4, 8, 12를 주어봤는데, 확실히 0일때는 이전 선형회귀와 똑같아진 것을 볼 수 있다. 그리고 람다값을 올리면서 점차 기울기가 줄고 회귀계수가 줄어드는것을 볼 수 있다.
편향, 페널티를 조금 더 주어서 이전 Train data에 모델이 과적합되지 않도록 조정을 해준 것이다.
그렇다면 어떤값이 최적의 값인지 알 수 있을까?
최적의 람다(, 알파)값을 찾아주는 RidgeCV
매번 for문을 돌려서 최적의 람다를 찾을때까지 기다릴 순 없다. 이를 위해 사용하기 편리한 RidgeCV를 이용하도록 한다. RidgeCV는 최적의 알파값을 찾고, CV라는 파라미터를 통해 cross validation을 자체적으로 진행해 성능에 대한 검토를 한다.
cv(cross validation)는 여기서 K-fold 교차 검증을 뜻하는 것인데, 이 원리는 간단히 말해 데이터를 train set과 test set으로 나누듯 지정된 k개로 나눈뒤 k번씩 자체적인 검증을 해 정확도를 올리기 위한 파라미터이다. 데이터가 부족해 교차검증이 힘든경우에도 이를 통해 자체적인 교차검증을 할 수 있다.
from sklearn.linear_model import RidgeCV
alphas = np.arange(1, 50, 1)
# RidgeCV모델 작성 람다는 1부터 50까지로 설정
model1 = RidgeCV(alphas = alphas, cv = 2)
model1.fit(X_train, y_train)
y_pred1 = model1.predict(X_test)
fig, ax = plt.subplots(1,2)
sns.scatterplot(data = df, x = df['Study time'], y = df['Score'], ax=ax[0])
sns.scatterplot(data = X_test, x = X_test['Study time'], y = df['Score'], color = 'orange',ax = ax[0]);
sns.scatterplot(data = df, x = df['Study time'], y = df['Score'], ax=ax[1])
sns.scatterplot(data = X_test, x = X_test['Study time'], y = df['Score'], color = 'orange',ax = ax[1]);
sns.lineplot(data = X_test, x = X_test['Study time'], y = y_pred1, color = 'red', ax = ax[0]).set_title('RidgeCVRegression')
sns.lineplot(data = X_test, x = X_test['Study time'], y = y_pred, color= 'red', ax = ax[1]).set_title('LinearRegression')
plt.show();
print('회귀계수:', model1.coef_[0])
print('최적알파:', model1.alpha_)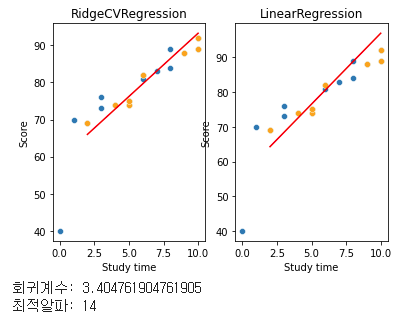
알파를 1에서 50까지로 설정하고 최적의 알파를 확인했는데 한번에 구할 수 있다. cv 파라미터를 조정하여 다양한 자체 검증을할 수 있는 매우매우 편리한 녀석이다, RidgeCV!
from sklearn.linear_model import RidgeCV
alphas = np.arange(1, 20, 1)
# 단순선형회귀모델 작성
model1 = RidgeCV(alphas = alphas, cv = 2)
model1.fit(X_train, y_train)
y_pred1 = model1.predict(X_test)
sns.scatterplot(data = df, x = df['Study time'], y = df['Score'])
sns.scatterplot(data = X_test, x = X_test['Study time'], y = df['Score'], color = 'orange');
sns.lineplot(data = X_test, x = X_test['Study time'], y = y_pred1, color = 'red')
sns.lineplot(data = X_test, x = X_test['Study time'], y = y_pred, color= 'red', linestyle="dashed", alpha = 0.5); 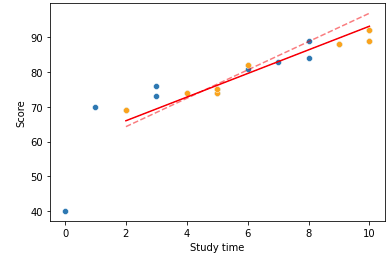
원래의 회귀선이 있던 위치가 점선이고, Ridge를 통해 편향을 더 주어 조정한 것이 실선 이다.