Linear Regression - 선형회귀의 평가 지표, MAE, MSE, RMSE, R Squared 정리

선형회귀의 다양한 평가 지표에 대한 공부했다.

선형회귀의 평가 지표

실제 데이터 표본과 예측데이터의 차이를 표현해 성능을 검토하기 위한 지표들이다. 풀어서 말하자면 Training 데이터로 학습한 회귀모델에 Test 또는 다른 새로운 데이터를 input했을 때, 모델이 예측한 값과 실제 표본 값을 바탕으로 다양한 방법으로 오차를 구해 성능을 평가하는 방법들이다.

MAE(Mean Absolute of Errors) 평균절대오차

$\operatorname {MAE}$=${\frac {1}{n}}\sum _{{i=1}}^{n}|{\hat {Y_{i}}}-Y_{i}|$

평균절대오차는 예측값 - 관측값들의 제곱이 아닌 절대값을 통해 음수를 처리한 뒤, 이들의 평균을 통해 구할 수 있다. 제곱을 하지 않기 때문에 단위 자체가 기존 데이터와 같아 회귀계수 증감에 따른 오차를 쉽게 파악할 수 있다.

MSE(Mean Square of Errors) 평균제곱오차

$\operatorname {MSE}$=${\frac {1}{n}}\sum _{{i=1}}^{n}({\hat {Y_{i}}}-Y_{i})^{2}$

굉장히 많이 사용하는 척도 중 하나인데, 제곱으로 인해 그 원래의 차이보다 다소 민감한 성능 평가가 될 수 있는 점을 고려하여 사용해야 한다.

평균제곱오차는 위 식과 같이 잔차제곱합(RSS)을 해당 데이터의 개수로 나누어서 구할 수 있다. 예측값 - 관측값(데이터값)의 제곱된 값의 평균을 구하는 것이다. 여기서 잔차의 제곱을 하는 이유는 잔차의 값이 음수가 될 수 있는 것을 방지할 수 있고, 제곱을 함으로써 오차의 민감도를 높이기 위함이다.

RMSE(Root Mean Square of Errors) 평균제곱오차제곱근

$\operatorname {RMSE}$ = $\sqrt{\operatorname {MSE}}$
평균제곱오차MSE에 루트를 씌워주어 비교에 좋도록 한 평가지표이다.

R2(R Squared Score) 결정계수

결정계수는 실제 관측값의 분산대비 예측값의 분산을 계산하여 데이터 예측의 정확도 성능을 측정하는 지표이다. 0~1까지 수로 나타내어지며 1에 가까울수록 100%의 설명력을 가진 모델이라고 평가를 하게된다.

관측치에서 예측치를 뺀 값의 제곱합에서 target 평균을 대상으로 하는 관측값의 잔차 제곱합을 나누어준 값을 1에서 빼주면 된다.

$SST$ (Sum of Squared Total): 관측치 - 예측값
$SSE$ (Sum of Squared Error): 관측값 - 예측값, 즉 잔차제곱합 RSS와 같은 의미이다.
$SSR$ (Sum of Squares due to Regression): 예측값 - 평균값

$\operatorname {R}^{2}$ = $\frac {\sum(\hat{Y}-\bar{Y})^2}{\sum(Y - \bar{Y})^2}$ = $\frac{SSR}{SST}$ or $1 - \frac {\sum(Y-\hat{Y})^2}{\sum(Y - \bar{Y})^2}$ = $1- \frac{SSE}{SST}$

$\operatorname {R}^{2}$ = $\frac {\sum(예측값 - 타겟평균값)^2}{\sum(관측값 - 타겟평균값)^2}$ or 1 - $\frac {\sum(관측값 - 예측값)^2}{\sum(관측값 - 타겟평균값)^2}$

말도 어렵고 어떤걸 따라야할지 모르겠지만, python 이용시, 결론적으로는 아래 식을 따르면 된다.

$\operatorname {R}^{2}$ = $1$ - $\frac {\sum오차^2}{\sum편차^2}$

그래서 이를 데이터셋에 단순선형회귀모델과 함께 구현하여 알아보았다.

import pandas as pd
import numpy as np
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression

# 공부시간에 따른 점수 표
df = pd.DataFrame({'Study time':[3,4,5,8,10,5,8,6,3,6,10,9,7,0,1,2],
		   'Score':[76,74,74,89,92,75,84,82,73,81,89,88,83,40,70,69]})

# 데이터셋 분리
train, test = train_test_split(df, test_size = 0.4, random_state = 2)
X_train = train[['Study time']]
y_train = train['Score']
X_test = test[['Study time']]
y_test = test['Score']

# LinearRegression 진행
model = LinearRegression()
model.fit(X_train, y_train)
y_pred = model.predict(X_test)


# 잔차 구하기
y_mean = np.mean(y_test) # y 평균값

# $\sum(y 예측값 - y 평균값)^2$ = 예측값에 대한 편차
nomerator = np.sum(np.square(y_test - y_pred)) 

# $sum(y 관측값 - y 평균값)^2$
denominator = np.sum(np.square(y_test - y_mean))
r2 = 1 - nomerator / denominator
r2

0.6632179284430186

r-square값을 수기로 계산하면 위와같이 0.6632이라는 결과를 가지게 된다. 이는 66% 정확도의 설명력을 가진 모델이라는 것을 입증해준다. 이렇게 수기로 하는 수고를 덜기 위해 만들어진 sklearn 라이브러리의 r2_score를 사용해보겠다.

from sklearn.metrics import r2_score
# r-square 함수사용
r2_score(y_test, y_pred)

0.6632179284430186

똑같은 결과가 나오는 것을 볼 수 있다. 이러한 $R^2$ 값은 위에서 언급한 바와 같이 분산을 기반으로 측정하는 도구이므로 중심극한정리에 의해서 표본 데이터가 많을수록 그 정확도 역시도 올라가게된다. PLOT을 이용해서 보면 그 예측 정확도가 달라지는걸 알 수 있다.

# 함수 작성
def linearregression(df, test_size):
  train, test = train_test_split(df, train_size = test_size, random_state = 2)
  X_train = train[['Study time']]
  y_train = train['Score']
  X_test = test[['Study time']]
  y_test = test['Score']

# LinearRegression 진행
  model = LinearRegression()
  model.fit(X_train, y_train)
  y_pred = model.predict(X_test)
# R2 계산
  print('R제곱 값:', r2_score(y_test, y_pred).round(2))
  print('Train data 비율: 전체 데이터 수의 {0}%'.format(i*100))
  print('Train data 수: {0}개'.format(len(X_train)))
# 플롯 그리기
  sns.scatterplot(x = df['Study time'], y = df['Score'], color = 'green')
  sns.scatterplot(x = X_test['Study time'], y = y_test, color = 'red');
  sns.lineplot(x = X_test['Study time'], y = y_pred, color = 'red');
  plt.show()

test_sizes = [0.1,0.2,0.3,0.4,0.5]
for i in test_sizes:
  linearregression(df, i)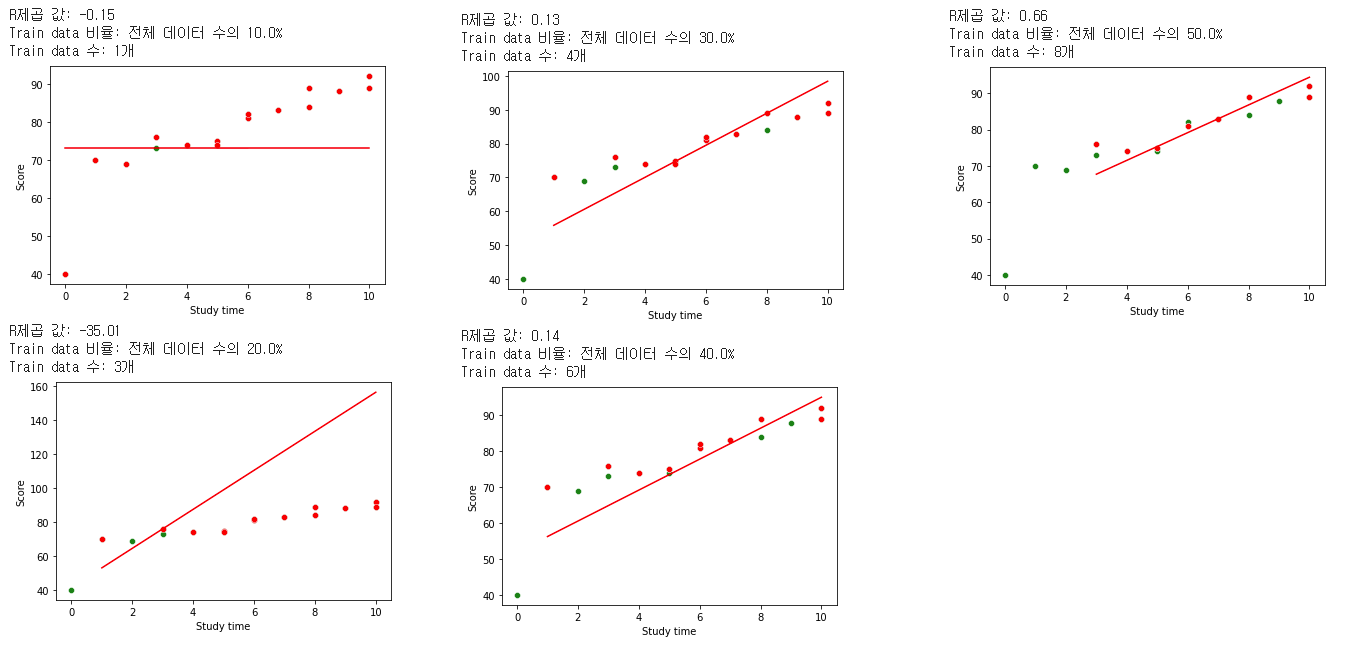

이미지와 같이 train data 수가 작을때는 오차가 너무 커서 음수가 나오다가도 데이터가 어느정도 이상이 되면 괜찮은 R제곱 값을 찾아가는 것을 확인 할 수 있다.

주의할 점은 데이터 수 뿐만 아니라, 다중선형회귀에서 특성이 많이 늘어날수록 R2 값이 오르는 경향도 있기 때문에, R2값에 대한 맹신은 하지 않도록 해야한다.