표본조사

• 통계적 추론을위해 표본조사를 통해 모집단에대한 해석을 진행한다.
• 전수조사는 실질적으로 현실에서는 불가능하기 때문데 표본조사를 한다.
• 표본조사는 반드시 오차가 발생하기 때문에 적절한 표본 추출방법이 필요한다.
• 표본과 모집단과의 관계를 잘 이해해야한다.

표본분포

• 표본조사의 목적은 모수(parameter), 즉 모평균, 모분산, 모비율 등을 예측하기 위함이다.
• 아래는 평균이 10, 표준편차가 3인 정규분포에서 표본을 10000회동안 10개씩 뽑았을 때 그 표본의 분포이다.
  

중심극한정리(central limit theorem)

• 모집단이 정규분포이면 n에 상관없이 표본평균의 분포는 정규분포를 따랐다.
• 모집단이 정규분포가 아닐 때는 표본추출시 n이 충분히 커야만 표본평균의 확률분포는 정규분포를 따른다.
• 0 부터 10까지의 수에서 n=3개를 10000번 뽑았을 때의 표본평균의 분포는 아래와 같은데 3은 너무작으므로 정규분포를 따른다고 보기힘들다.
  
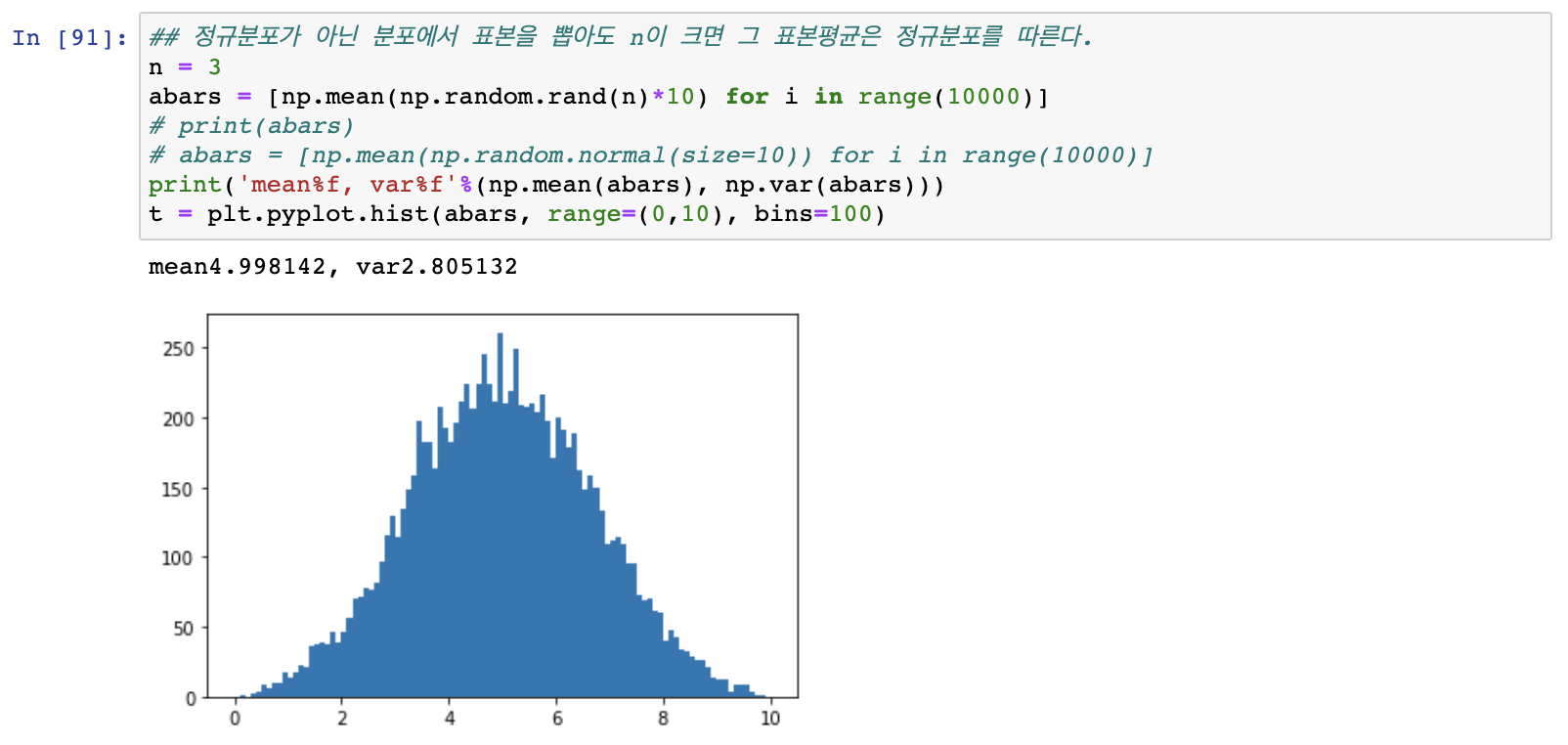
• n=30 으로 바꿔주면 조금은 더 정규분포와 가깝게 보인다.
  

지수함수 표본 평균의 분포

• 평균이 1/3인 지수함수(사건발생하기까지 3시간이 걸린다고 볼수있음)에서 n=2 개를 뽑았을 때 아래와 같다.
  
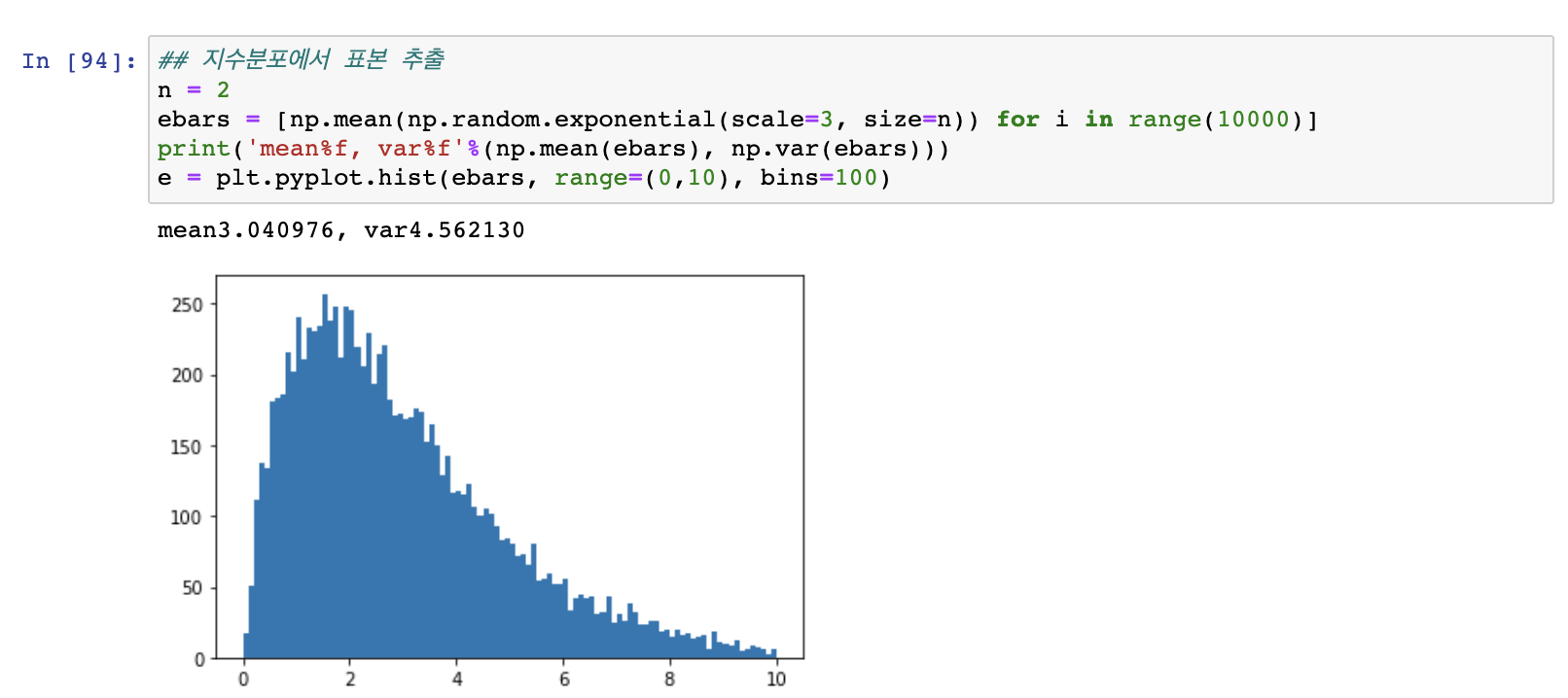
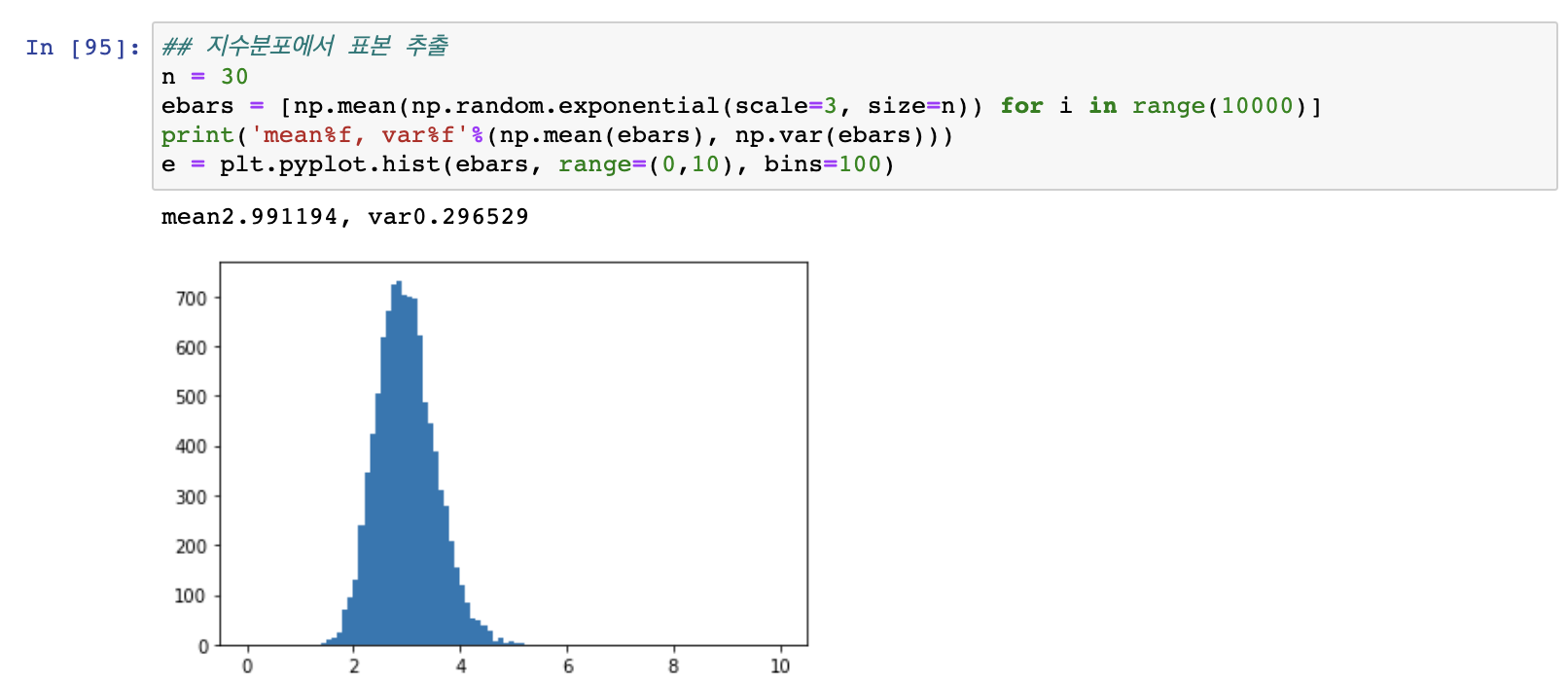
• n= 30으로 충분히 늘려주면 마찬가지로 지수분포에서 표본을 뽑아도 그 표본의 평균은 정규분포가 된다는 것을 알 수 있다.
  
  

추정

모평균 추정

• 점추정 : 표본평균이 점 추정값이 됨. 하지만 점추정만으로는 모집단을 제대로 예측하기 어렵다. 따라서 구간추정을 이용한다.
• 구간추정
  • 표본의 크기가 클때 중심극한 정리를 사용한다.
  • 만약 95%의 신뢰구간을 가진다고하면 모집단에서 표폰을 100번 뽑았을때 95번은 표본평균이 95%에 해당하는 구간안에 존재할 것이다라는 의미
  • 표준오차 : 표준편차 s(아래그림)를 표본의 수의 제곱근으로 나누어준 것이다. 원래는 s가 아닌 모집단의 표준편차인 시그마를 사용해야하지만 값을 모르므로(우리가 추정해야하는 값이므로) s를 사용한다.
    
    
    
    

모비율 추정

• 점추정 : 모집단에서 n개의 표본을 뽑았을 때 그 안에서 특정 속성을 갖는 표본의 개수를 확률변수 x라하면 모비율을 점추정량 p'는 = x/n이다.
• 구간추정
  
  

검정

• 아래에서 X'와 M, M0각각이 의미하는바가 조금 헤갈렸었는데 강의를 다시들어보니 제대로 이해할 수 있었다.
  • X' : 표본의 평균 171.3cm
  • M : 이번에 들어온 1학년 모집단의 평균(여기서는 검정을 위한 값)
  • M0 : 기존에 알려진 1학년 모집단의 평균 170.5cm
• 여기서 귀무가설을 기각한다는 것은 X'를 통해 이번에 들어온 1학년이 기존 1학년보다 크다고 할 수 있을 때이다. 따라서 귀무가설을 기각하기위해서는 X'가 높은 확률로 큰값이 나와야한다.
  
  
  

모평균의 검정

• 대립가설이 참인경우는 새로운 가설이 맞는 경우를 의미하며 즉, 아래에서 뮤와 뮤제로가 같은경우를 제외한 나머지 경우이다.
  
  아래에서 검정하고자하는 것은 M(사료운 사료를 도입한 후 계란의 모평균)를 통해 새로운 사료의 효과이다. 만약 M이 기존의 모평균 무게인 10.5와 같다면 새로운 사료와는 상관없으므로 귀무가설이 맞는 것이고 그렇지않으면 귀무가설을 기각할 수 있다.
  
  마찬가지로 아래에서는 광고가 맞는지 틀린지 M를 통해 검증하기위한 것으로 실제 무게가 홍보하는 10.5와 같다면 귀무가설이 맞는것이고 그렇지않으면 귀무가설을 기각할 수 있다.
  

검정통계량

• 검정통계량은 아래의 Z값며 Z의 절대값이 아래의 기각역 이상일 때 귀무가설을 기각(대립가설 채택)할 수 있다.
  

기각력

교차엔트로피

자기정보(self-information)

• 자기정보는 사건을가지고 정보를 표현한 것이고 아래와 같이 정의한다.
• 확률이 높지않는 사건일수록 많은 정보를 포함하고있다.
  
  

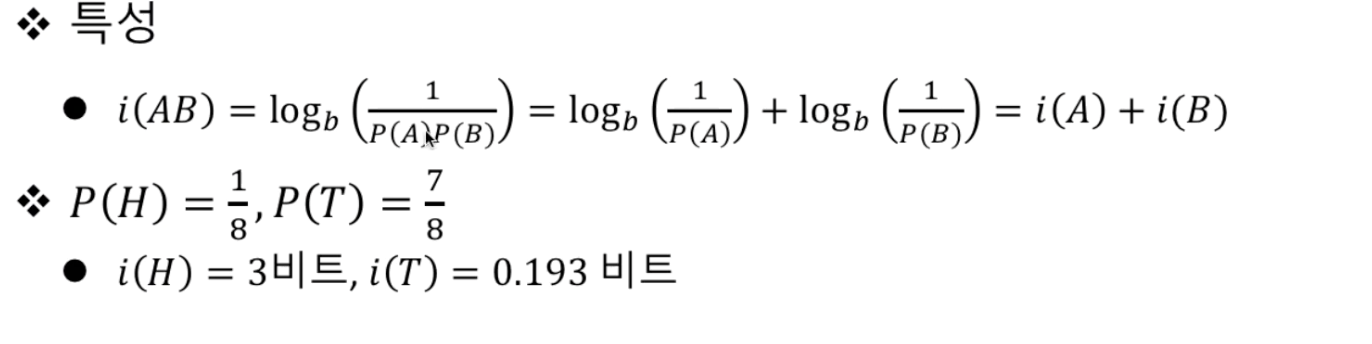
엔트로피(entropy)

• 자기 정보의 평균
  
• 엔트로피의 활용
  

교차엔트로피

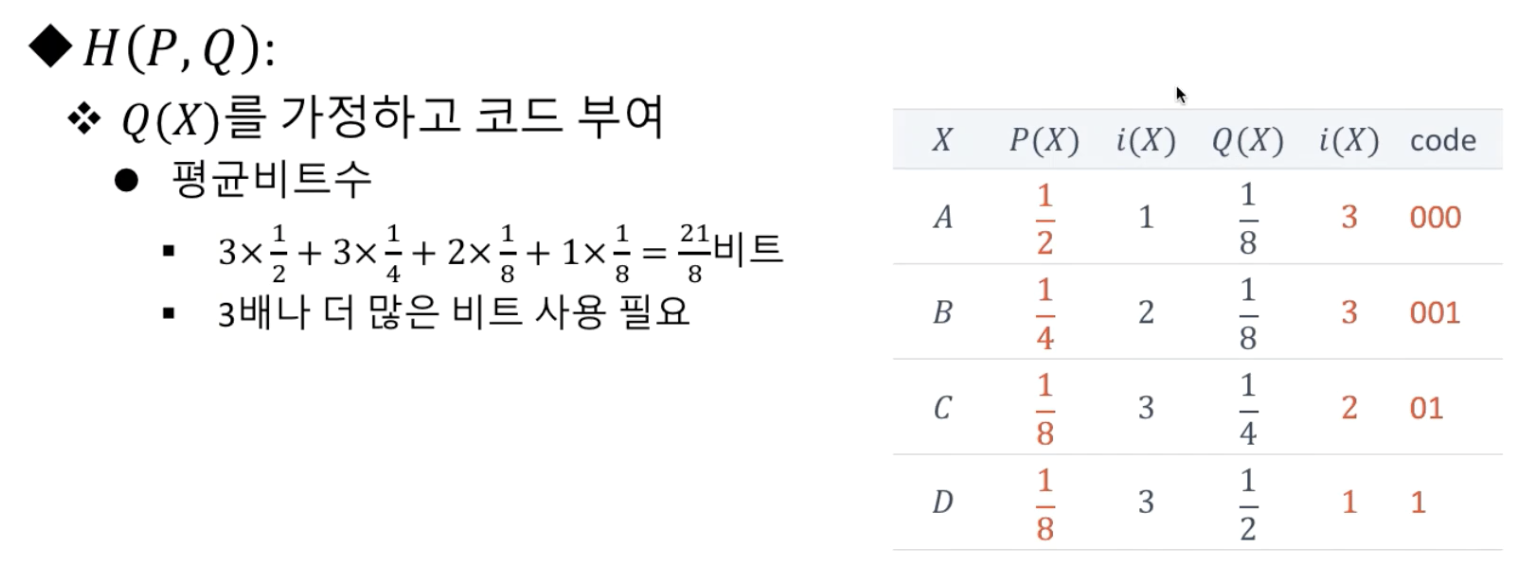
• 두개의 확률분포 P와 Q를 가질때
  
  
• 아래를보면 확률분포 Q를 가정했을 때 P를 가정했을 때보다 더 많은 비트를 사용하므로 평균비트수가 큼을 알 수 있다.
  

손실함수

• 기계학습에서 각 대상이 정답일 확률은 보통 1이아니다.(100%가 아니라는 의미) 따라서 확률이 1로써 정답일 때와 얼마나 다른지 측정하는 함수를 손실함수라고한다.
  
  그리고 손실함수를 구할 제곱합을 통해 구하게되면 학습속도가 느리므로 속도문제를 해결하기위해 교차엔트로피를 사용한다.
  
• 아래처럼 실제상황과 가깝게 예측할수록 교차엔트로피 값이 0에 가깝게나온다.