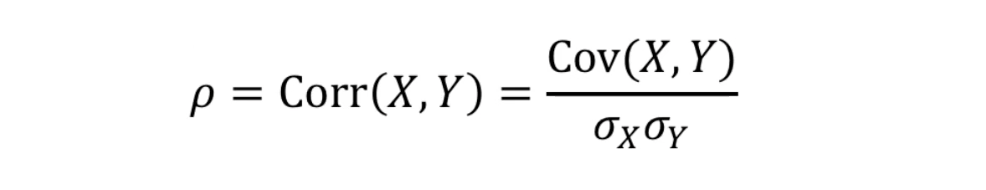확률(probability)


확률의 덧셈법칙
- 아래와 같이 사건 A나(or조건) B가 일어날 확률을 구하려면 각각의 확률을 더하고 교집합이 되는 확률을 빼주어야한다. 이때 교집합이 없다면 A와 B를 서로 배반(mutually exclusive)한다고한다.

조건부 확률(conditional probability)
- 어떤 사건 A가 일어났을 때 다른 사건 B가 일어날 확률
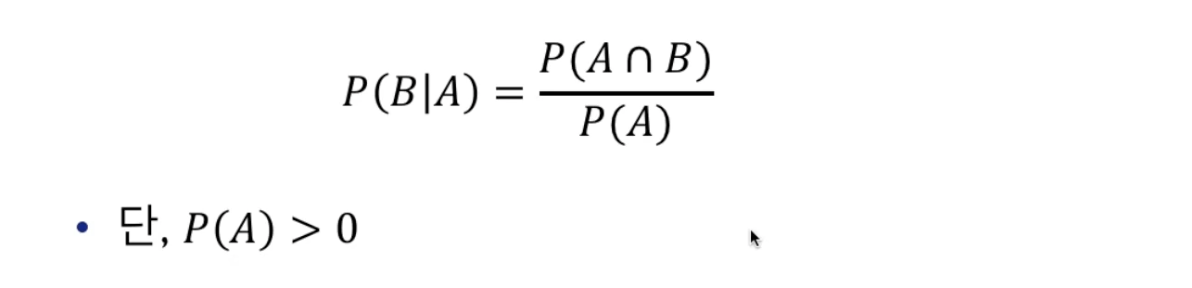
확률의 곱셈법칙
- 어떤 사건 A와 B가 동시에 일어날 확률은 A가 일어났을 때 B가 일어날 확률과 A의 확률의 곱이된다.
- 이때 사건 A와 B가 서로 영향을 주지않을 때 두 사건을 독립이라고하며 두 확률의 교집합은 곱과 같다.
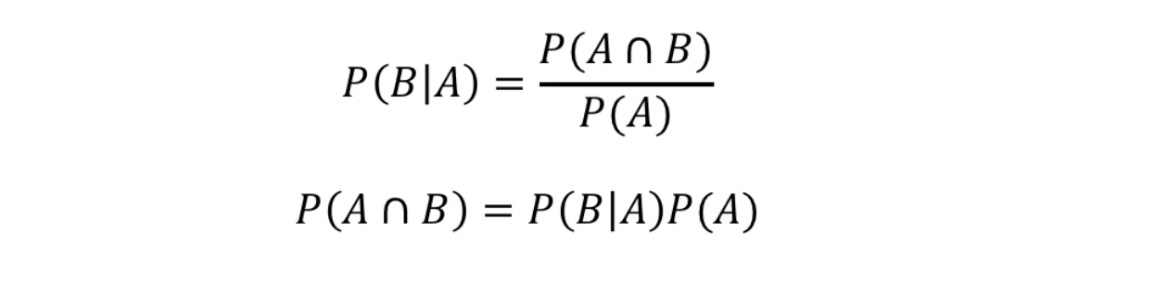
확률분포
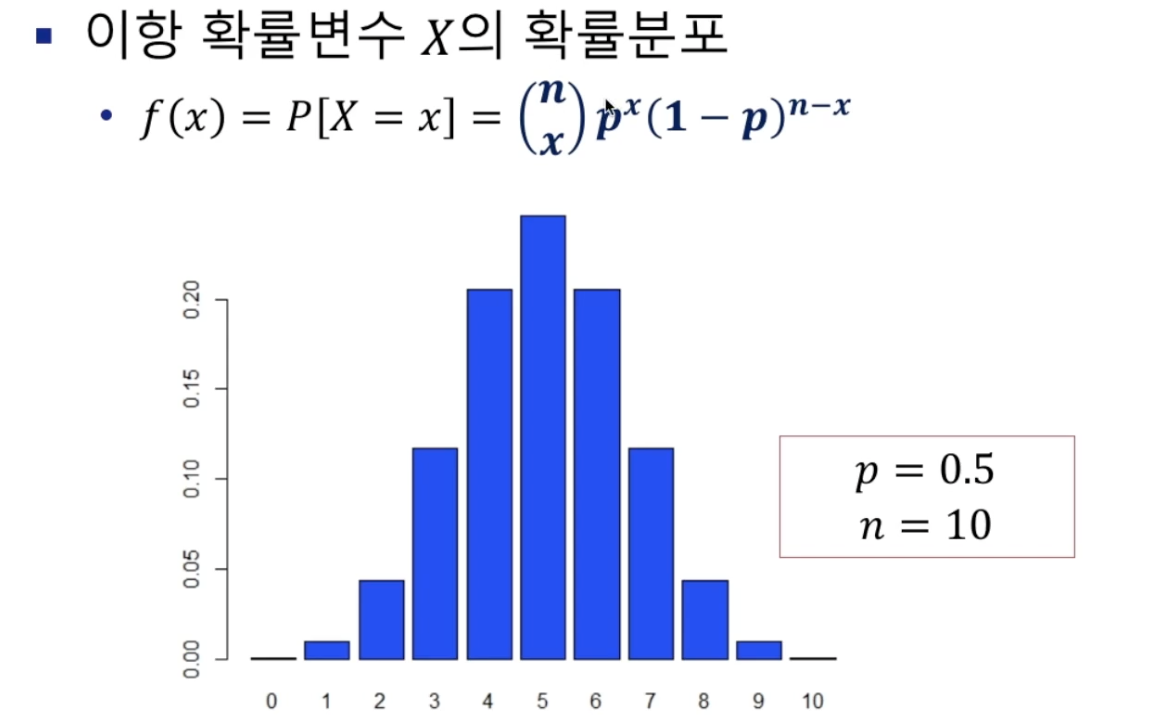
이항분포
베르누이 시행(Bernoulli trial)
- 성공/실패 두가지만 가지는 실험(ex 동전던지기)
- 연속이아닌 이산확률의 시행
- 성공확률 p
확률변수 X
- n번의 베르누이 시행에서 성공 횟수를 의미
- 이항확률변수라고 함
이항분포(binomial distribution)
- 이항확률변수의 확률분포
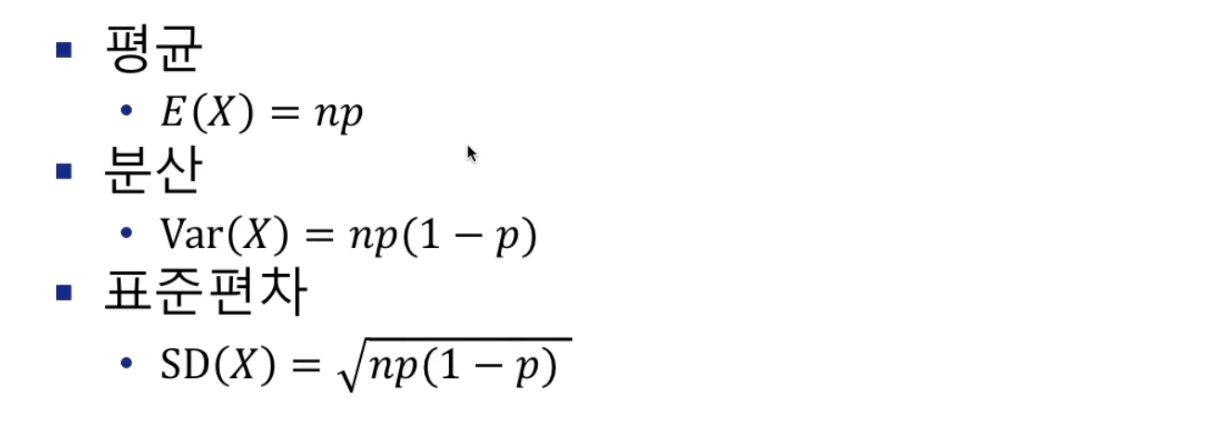
정규분포
- 연속확률 변수의 확률분포
- 확률밀도함수 (probability density function : f(x))
- 확률변수 X의 분포를 나타내는 함수로 확률변수 X가 구간 [a, b]에 포함될 확률을 의미한다.
- f(x)가 x의 확률을 제공해주는 것이 아니다.
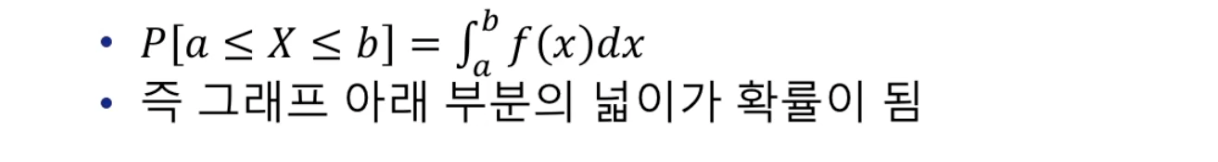
- 정규분포의 확률밀도함수
- 표준정규분포 : 평균이 0, 표준편차가 1인 정규분포
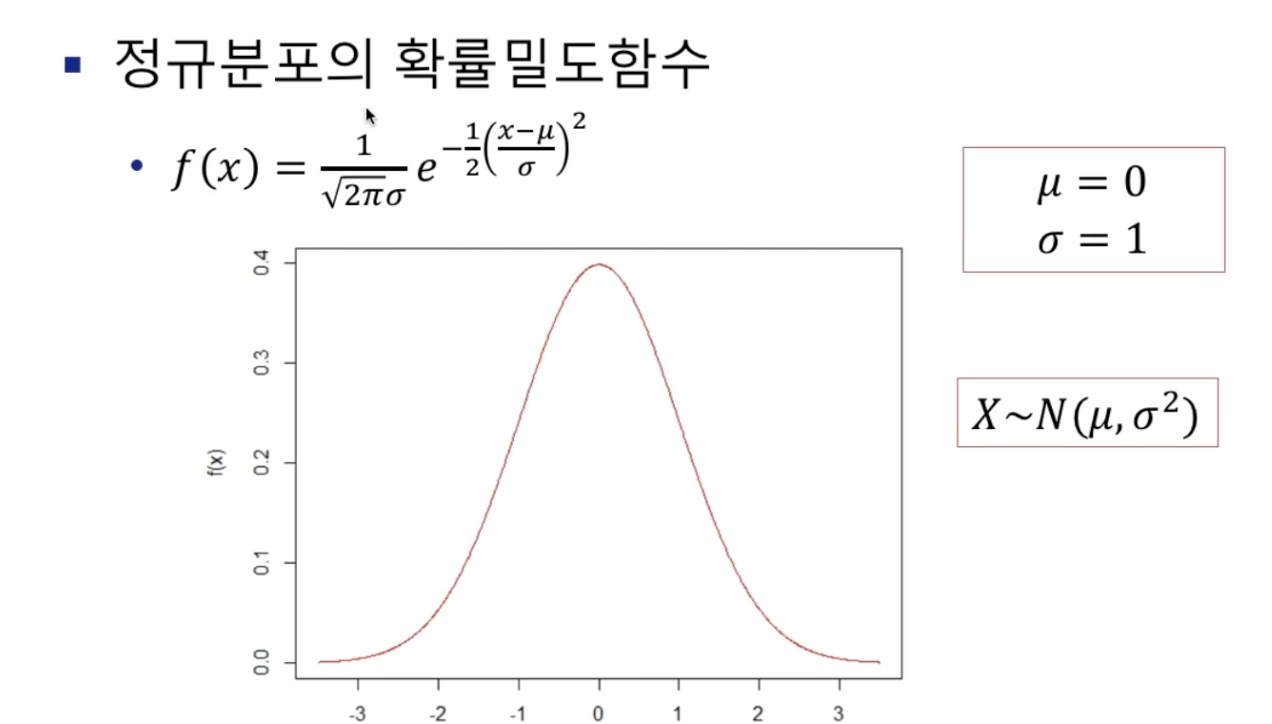
- 표준정규분포 : 평균이 0, 표준편차가 1인 정규분포
- 아래의 변환을 통해 정규분포의 확률변수를 표준정규확률변수 Z로 변환할 수 있다.

포아송 분포(Poisson distribution)
- 일정한 시간단위 또는 공간단위에서 발생하는 이벤트의 수의 이산확률분포
- 보통 낮은 확률의 분포다.
- 웹사이트 방문하는 방문자 수, 전기선 100m당 발생하는 결함 수, 쇼핑몰 구매고객 수
- 포아송 분포의 확률분포함수(확률질량함수)는 아래와 같다.

지수분포(exponential distribution)
- 포아송 분포를 따르는 어떤 사건이 발생할 때 어느 한 시점으로부터 이 사건이 발생할 때까지 걸리는 시간에 대한 확률 분포
- 예를들어 웹사이트 시간당 평균접속자가 3명이라할 때 1명의 접속자가 발생할 때까지 걸리는 시간은 1/3이다.

from scipy import stats
## 이항분포 : 3개를 뽑을 때 적어도 하나 이상의 성공이 발생할 확률, 성공확률은 0.2
1- stats.binom.cdf(0, n=3, p=0.2)
## X~N(4, 3^2)일때 P[X <=4]=?
stats.norm.cdf(4, loc=4, scale=3)
## X~N(4,3^2)일때 P[4 <= X <= 7] =?
stats.norm.cdf(7, loc=4, scale=3) - stats.norm.cdf(4, loc=4, scale=3)
## 포아송 분포 : 웹사이트 시간당 평균접속자 3명, 1시간 동안 접속자 수가 2명 이하일 확률은?
stats.poisson.cdf(2, mu=3)
## 지수분포 : 시간당 3명 접속, 30분 이내에 올 확률?
stats.expon.cdf(0.5, scale=1/3)확률변수(Random variable)
- 표본공간(Sample Space)의 표폰을 실수값에 맵핑시키는 함수이다.
- 랜덤한 실험결과에 의존하는 실수
- 확률변수의 종류
- 이산확률변수
- 연속확률변수
확률분포(Probability Distribution)
- 확률 변수가 가질 수 있는 값에 대해 확률을 대응시켜주는 관계
- 확률분포의 표현은 다양할 수 있다 : 그래프, 표, 함수

이산확률변수
- 이산확률변수(discret random variable) : 확률변수가 취할 수 있는 모든 수 값들을 하나씩 셀 수 있는 경우(예 주사위, 동전)



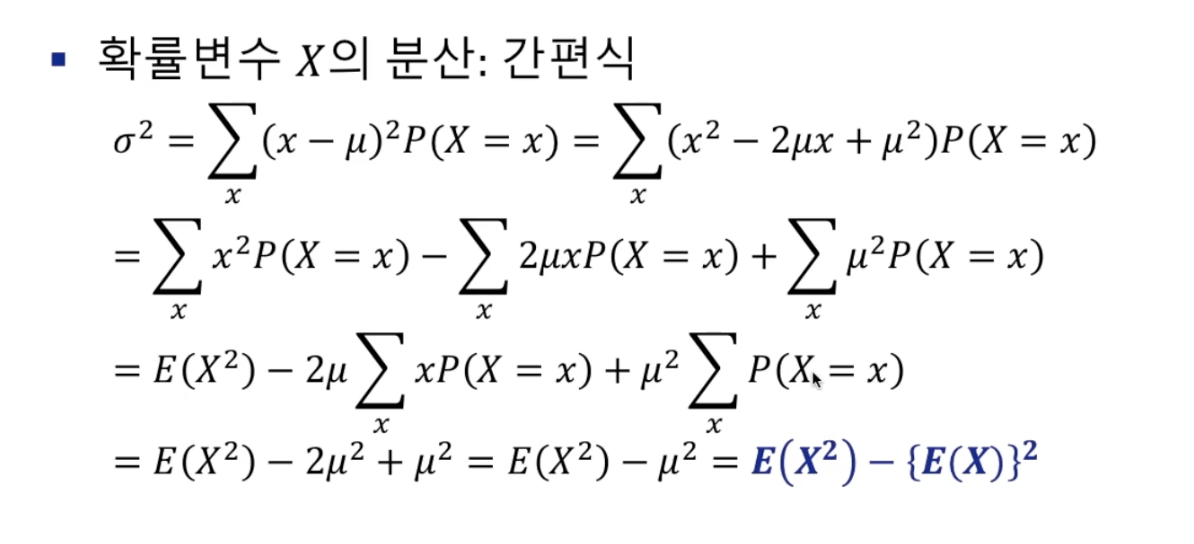
결합확률분포(joint probability distribution)
- 두개 이상의 확률 변수가 동시에 취하는 값들에 대해 확률을 대응시켜주는 관계
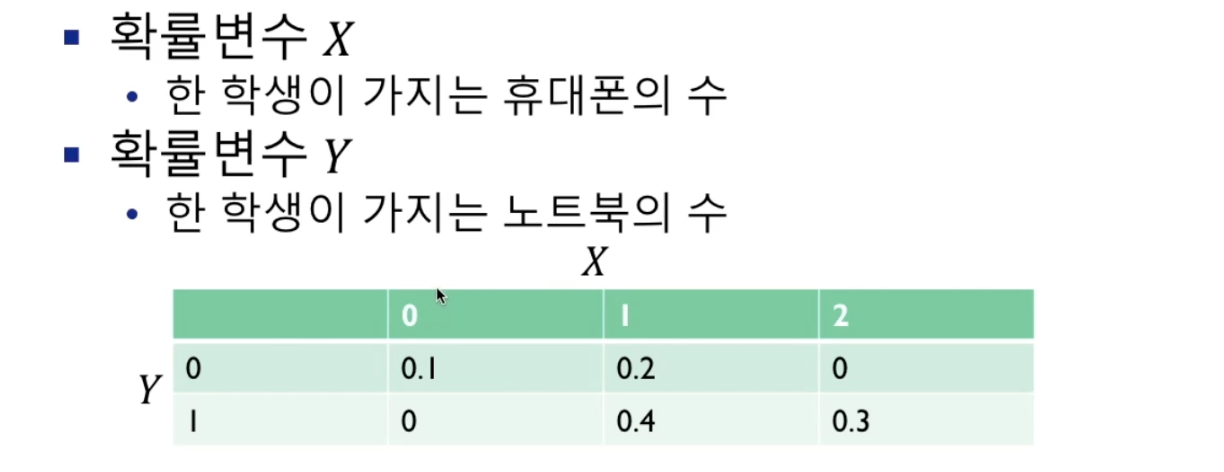

공분산(covariance)
- 키와 몸무게는 일반적으로 키가 큰사람이 몸무게도 크기 때문에 두 변수간에는 연관이 있다고 볼 수 있지만 키와 수학성적은 크게 연관이 없다. 이렇듯 공분산을통해 두개 이상의 변수의 값과 평균의 차를 곱해 그 상관관계를 알 수있다.

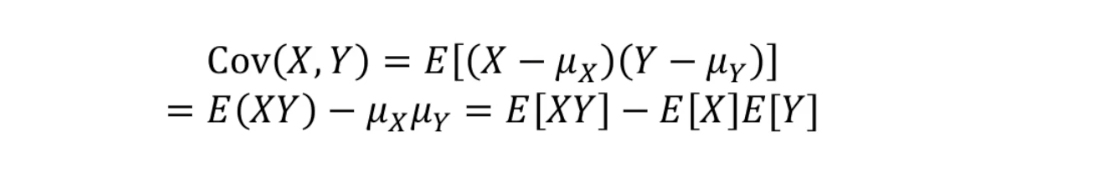
상관계수(correlation coeffient)
- 공분산은 확률변수의 절대적인 크기에 영향으 받기 때문에 이 영향을 없애줄 필요가 있다.
따라서 각 변수의 표준편차로 나눈값을 상관계수라고한다.