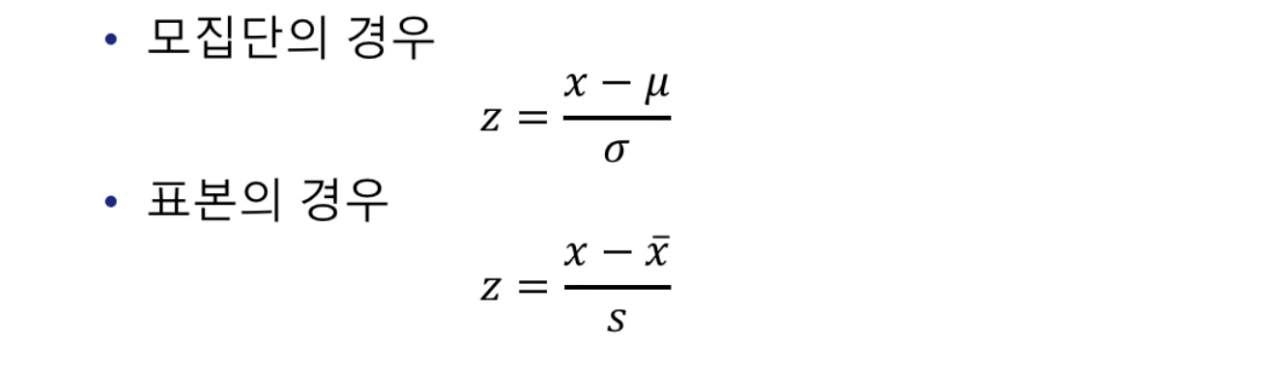벡터와 직교분해

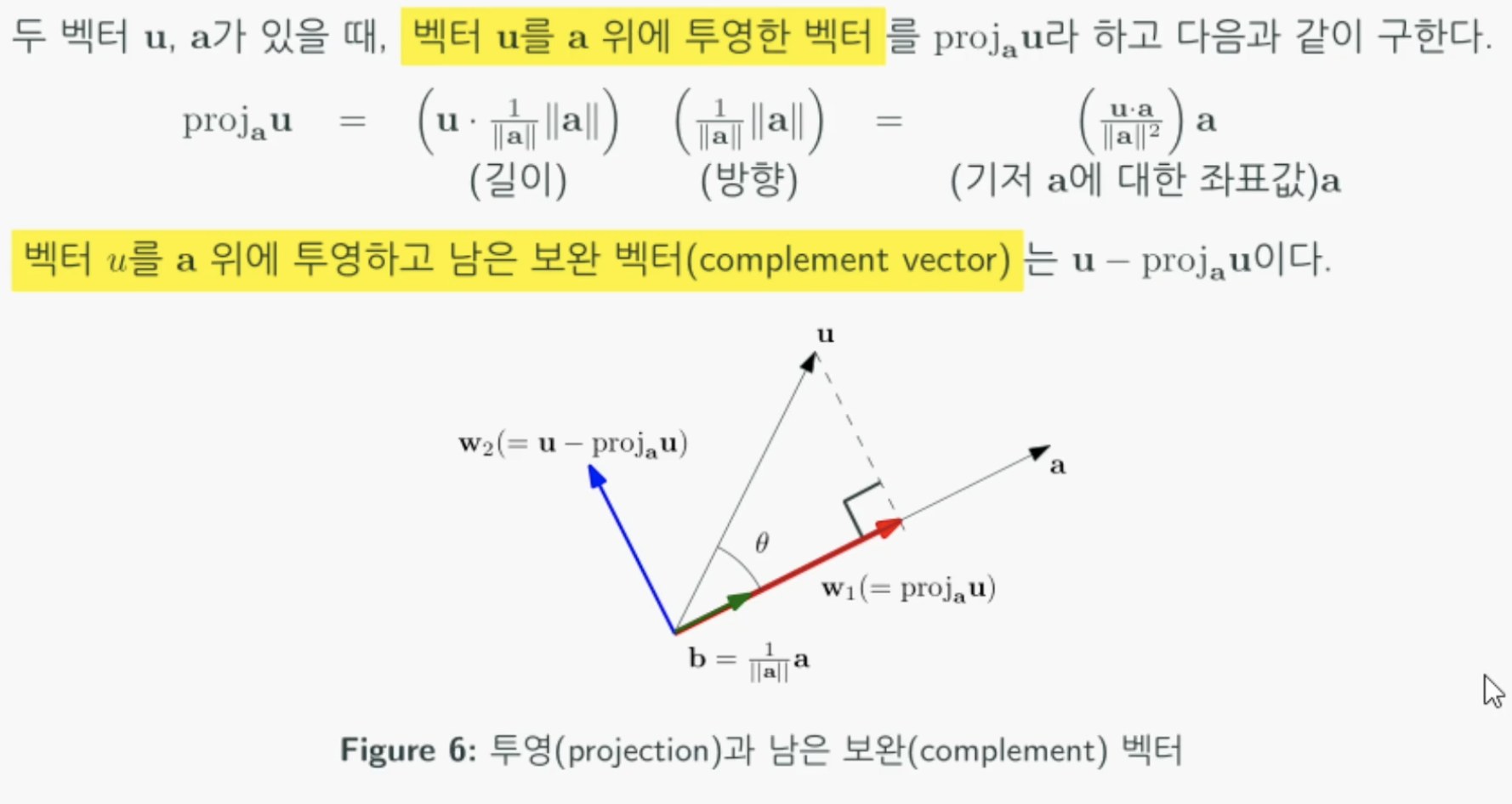
벡터의 직교분해를 이해하기위해서는 투영(projection)의 개념을 알아야한다.
아래 그림과 같이 벡터 u를 벡터 a에 투영한 결과를 w1이라고하고 u에서 그 w1벡터를
빼면 w2가 남는다. 이 때 w2를 보완 벡터라고 한다.

아래와 같이 행렬의 각 열벡터가 서로 직교하면 직교행렬이라하고 오른쪽처럼 직교행렬의 열벡터 크기가 1이면 정규직교행렬이라한다.

직교행렬을 사용하면 투영을 이용해 역행렬을 사용하지않고 쉽게 계산이 가능하며 직교행렬이므로 구하려는 x의 계산은 병렬처리 가능하다.
벡터 x의 각각의 원소는 벡터b를 좌표계인 A의 각 열벡터에 투영하여 얻을 수있다.

또한 A가 아래와같이 정규직교행렬이라면 심플하게 b와 A의 각 열벡터를 내적함으로써 x벡터를 얻어낼 수 있다.

QR 분해

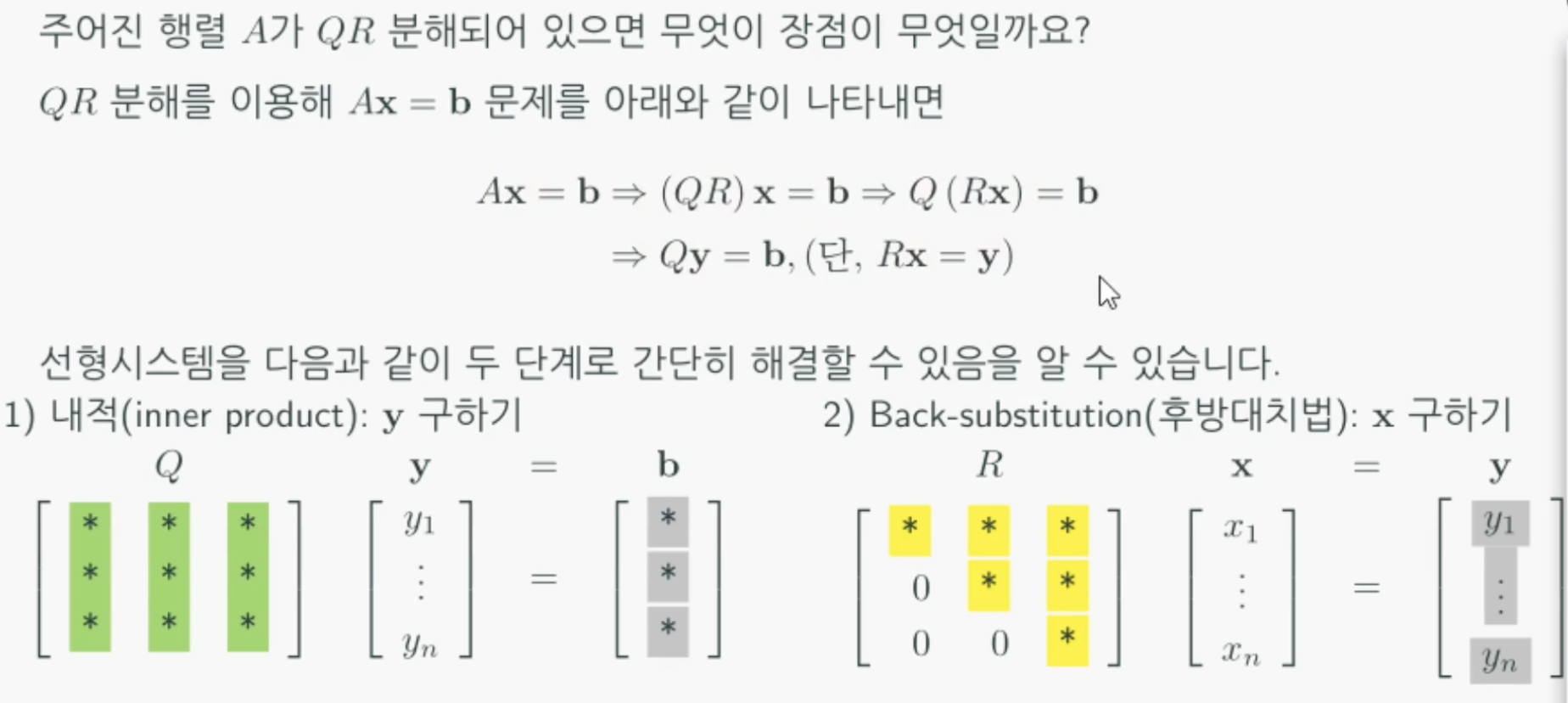
QR분해는 어제배운 LU분해와 비슷하게 벡터 A를 분해해서 해를 구하는 방법으로 다른점은 Q는 정규직교행렬, R은 상삼각행렬(upper triangular matrix)로 분해하는 것이다. 이렇게 분해하게되면 정규직교행렬의 장점을 사용해 쉽게 내적을이용해 Rx값을 구할 수 있고 가우스소거법의 후방대치법을 사용해 x를 구할 수 있다.


QR분해는 그람-슈미트 과정(Gram-Schmidt process)를 행렬로 코드화 한 것이다.
이렇듯 QR분해를 이용하는 목적은 다음과 같다.

SVD, PCA

특이값분해(Singular Value Decomposition, SVD)

• 주어진 행렬을 아래와 같은 형태의 세 행렬 곱으로 분해하는 것
• 이전까지 배운 분해법은 정방행렬만 분해가 가능하지만 특이값분해는 m x n행렬과같은 일반적인 행렬의 분해도 가능하다.
  

위 그림만 보고 직관적으로 이해하기는 쉽지 않은 것 같다. 예를들어 3x2의 A행렬이 주어졌다고하자.
각 열벡터가 나타내는 좌표는 아래그림의 맨 오른쪽과 같고 두 벡터는 거의 같은 방향을 바라보고있다.
그리고 어떤 2차원 행렬(맨왼쪽그림)이 있는데 이를 transpose를 취하면 회전되어 왼쪽에서 두번째 그림이된다. 그 후 D만큼 확대/축소되고 U의 각 열벡터로 축을 회전해주면 A가 된다.

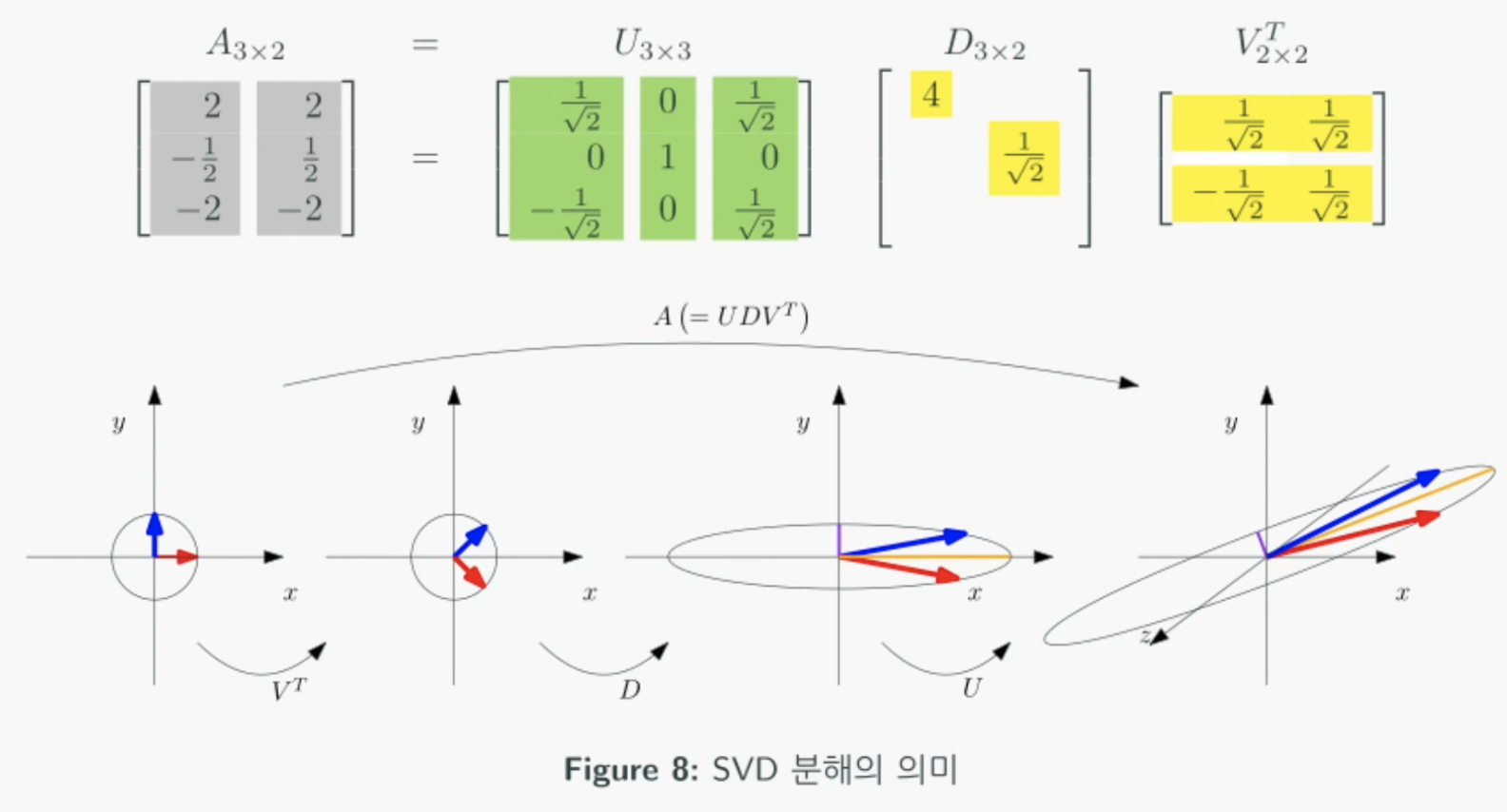
여기서 직교행렬(orthogonal matrix)과 대각행렬(diagonal matrix)의 기하학적 의미를 알면 조금 더 쉽게 이해할 수 있다. 직교행렬 곱의 기하학적 의미는 회전변환이고 대각행렬 곱의 기하학적 의미는 스케일곱이다. 실제로 간단한 직교행렬과 대각행렬 곱을 해보면 알 수 있다.


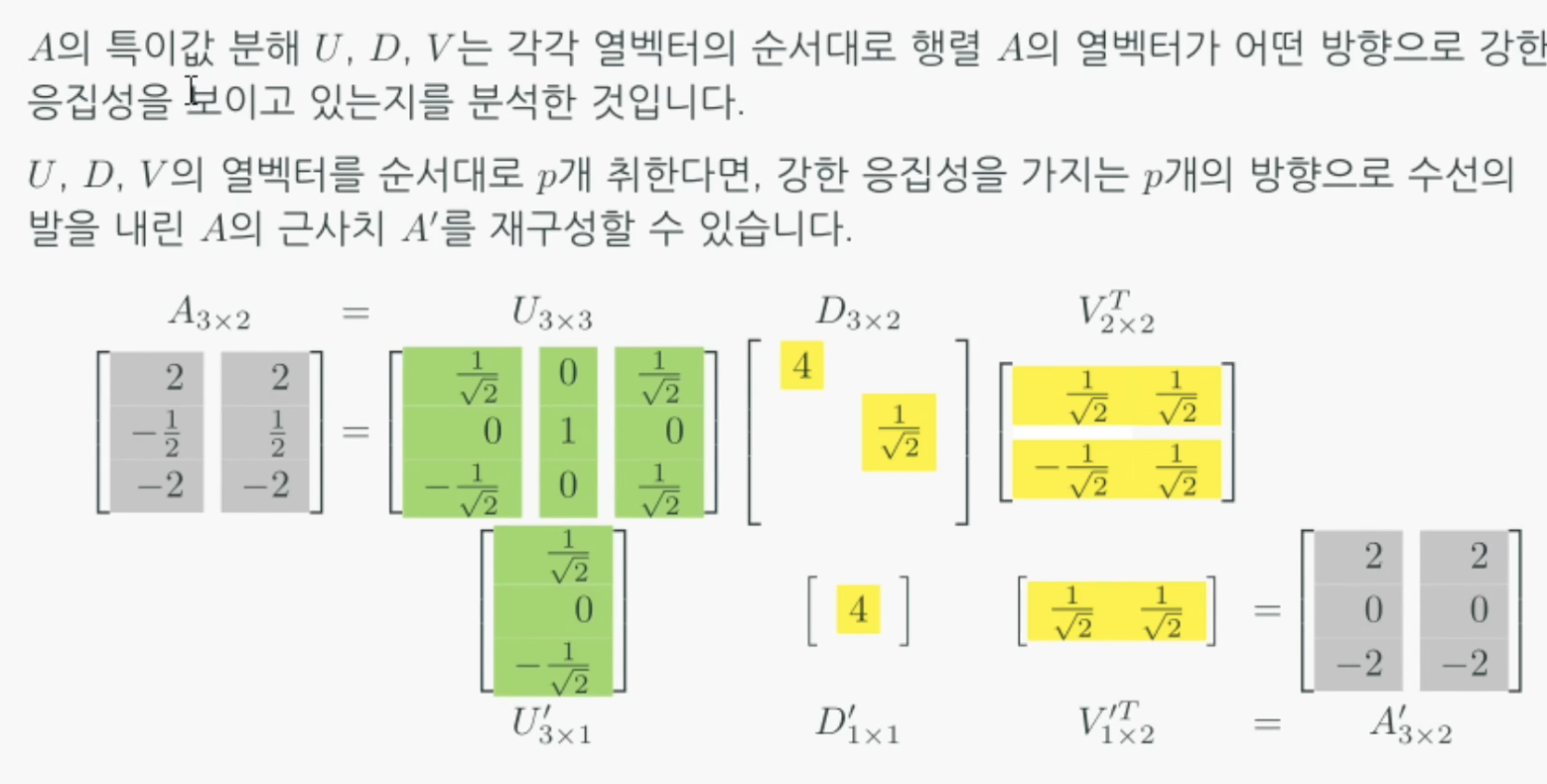
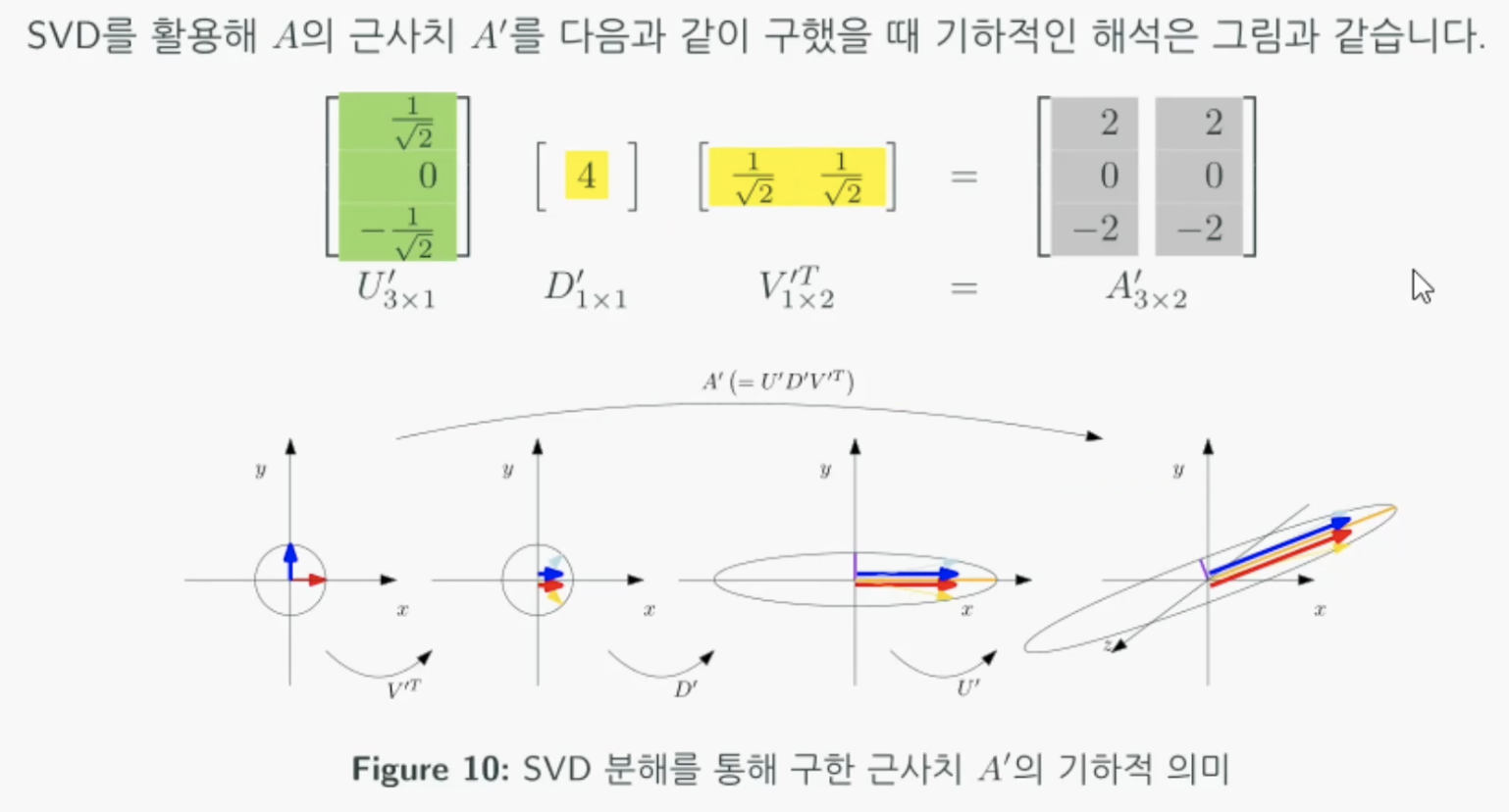
특이값 분해를하는 목적은 원래 행렬에서 응집성이 높은 정보만 남기고 나머지는 제거한 행렬을 얻기 위함이다. 즉 데이터의 응집성이 높은 것만 선택적으로 위하기 위함이다.

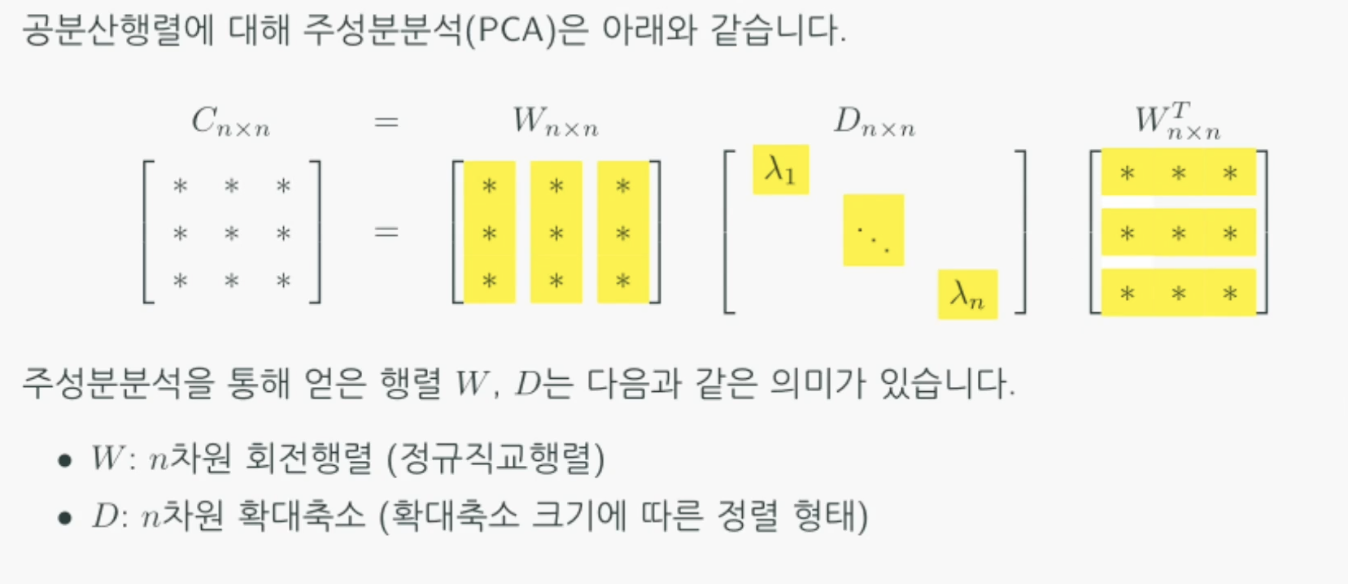
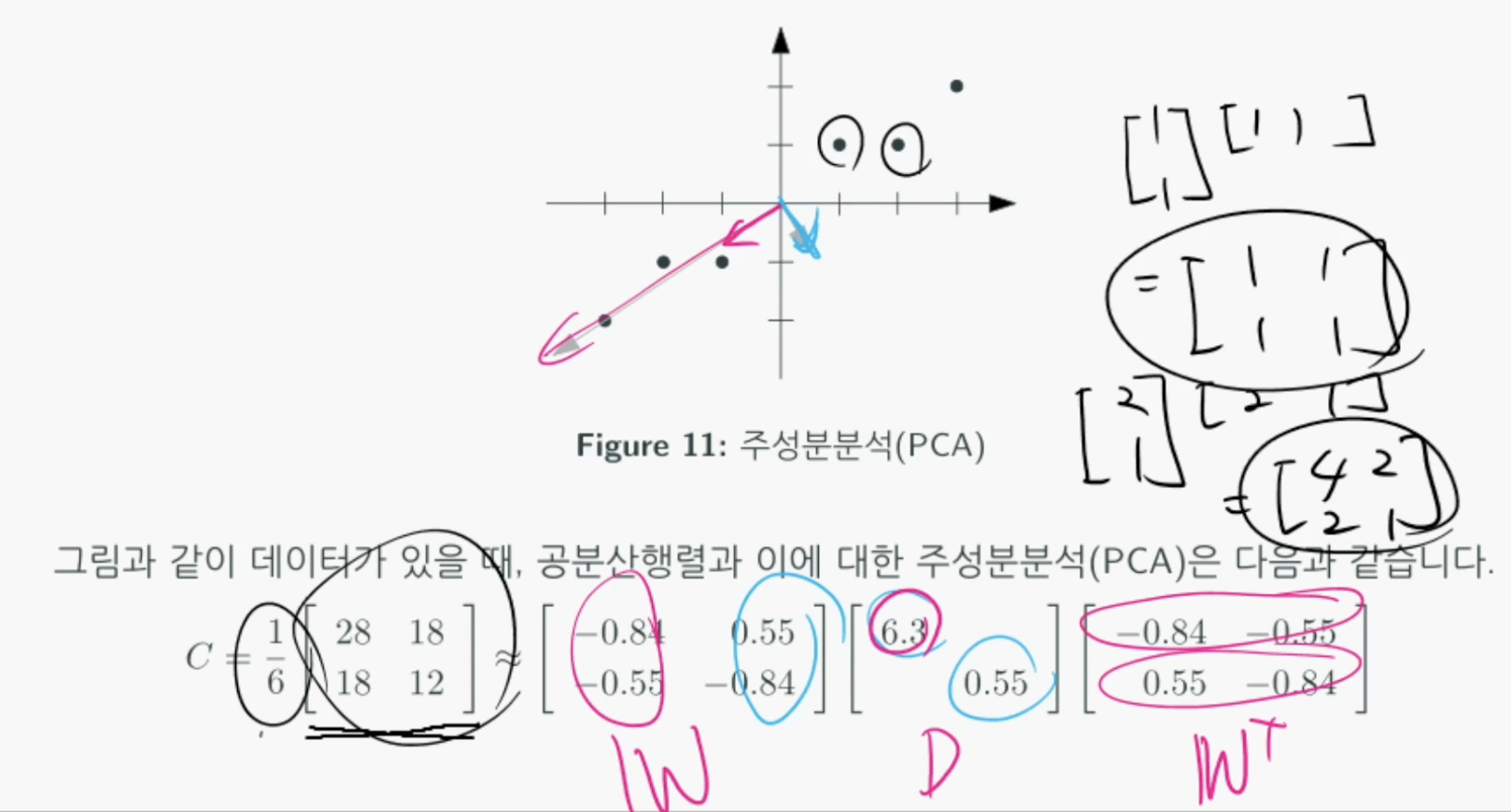
주성분 분석(Principal Component Analysis, PCA)

• 주성분분석(PCA)는 다수의 n차원 데이터에 대해 데이터 중심으로부터 데이터의 응집력이 높은 n개의 직교 방향을 분석하는 방법이다.
  

외적

• 외적은 두 벡터의 곱으로 내적과 다르게 결과값이 스칼라가아닌 벡터를 갖는다.
  

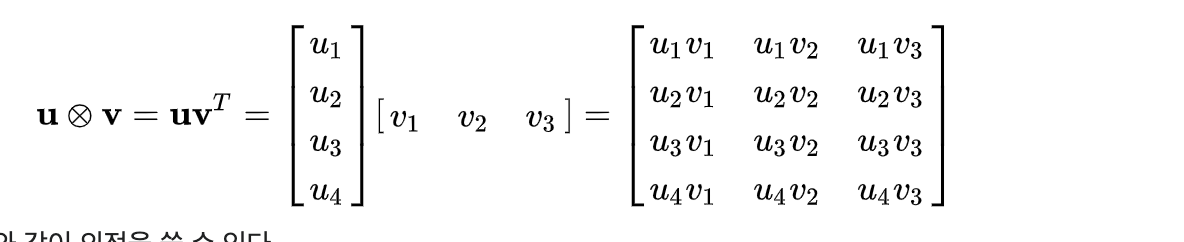
공분산행렬

• 데이터 구조를 설명해주며 특정 쌍의 변동이 얼마다 닮았는지를 행렬에 나타낸다.
• 쉽게말해 서로 다른 변수간에 관계를 분산과 공분산으로 나타낸 행렬을 공분산 행렬이라한다.
• 변수간
  

PCA도 이름에서 알 수 있듯이 주성분인 응집력이 높은 정보만 취하기 위함이다. 모든 데이터에대해 외적으로 차원을 증가시키고 평균을 구한 후(공분산) 주성분분석(PCA)를 한다.

벡터공간과 최소제곱법

벡터공간

연산에 닫힌 집합(set)

• 집합에서 어떤 원소를 뽑아 연산을 수행햇을 때 결과가 여전히 집합에 포함되어있다면 해당 집합은 연산에 닫혀있다고한다.
  

공간(Space)

• 덧셈연산과 스칼라 곱 연산에 닫혀있는 집합을 공간이라고한다.
  

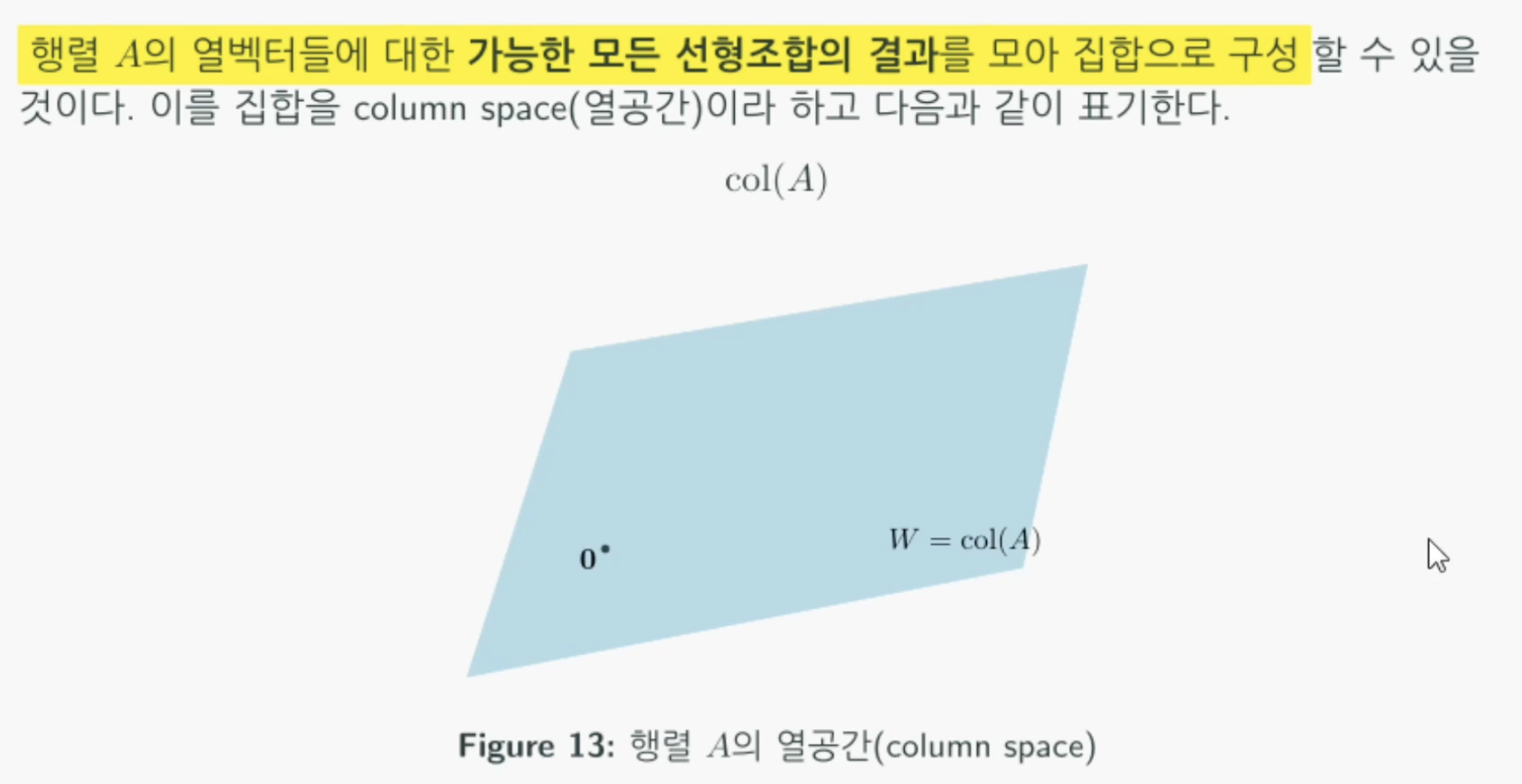
열공간(Column Space)

• 특정 행렬의 열벡터에대해 가능한 모든 선형조합으로 결과를 만든 집합을 열공간이라고한다.
  
  

최소제곱법(least square method)

• Ax = b에서 x의 해가 존재하지않지만 그래도 이 x를 최선으로 만족하는 해를 찾는 방법이다.

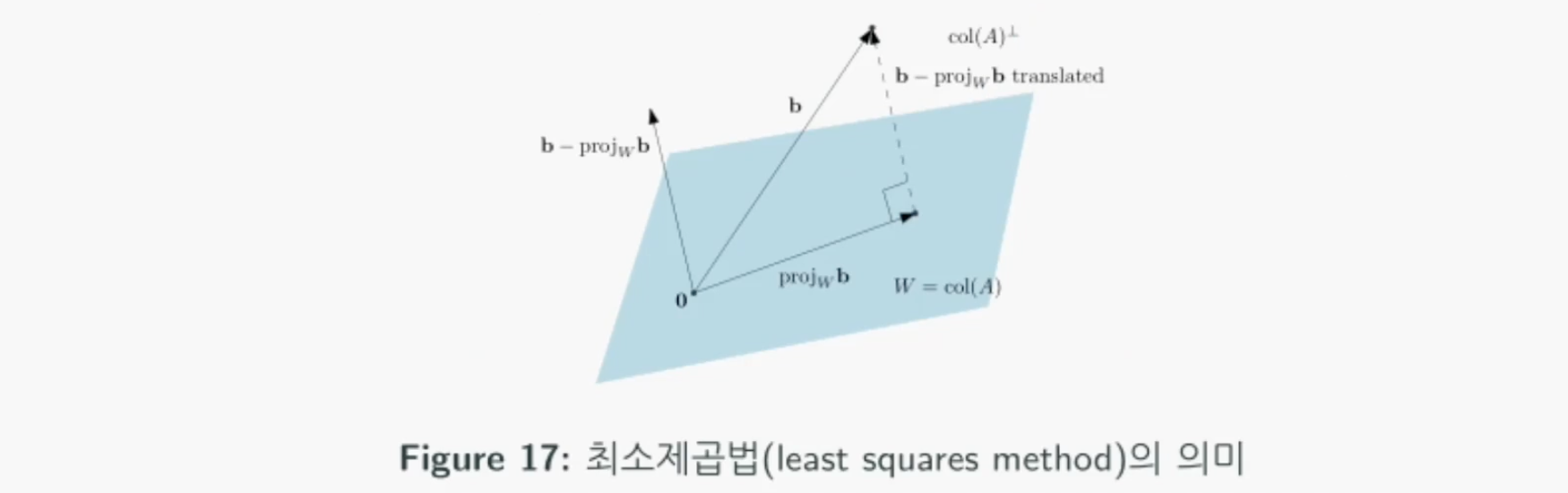
• 아래그림에서 b를 만족하는 x가 없으므로 b의 projection을 만족하는 해를 찾을 때 b - b(proj)의 제곱길이를 최소화시키는 해를 찾는 것을 의미하므로 최소제곱법이라고 부른다.
  

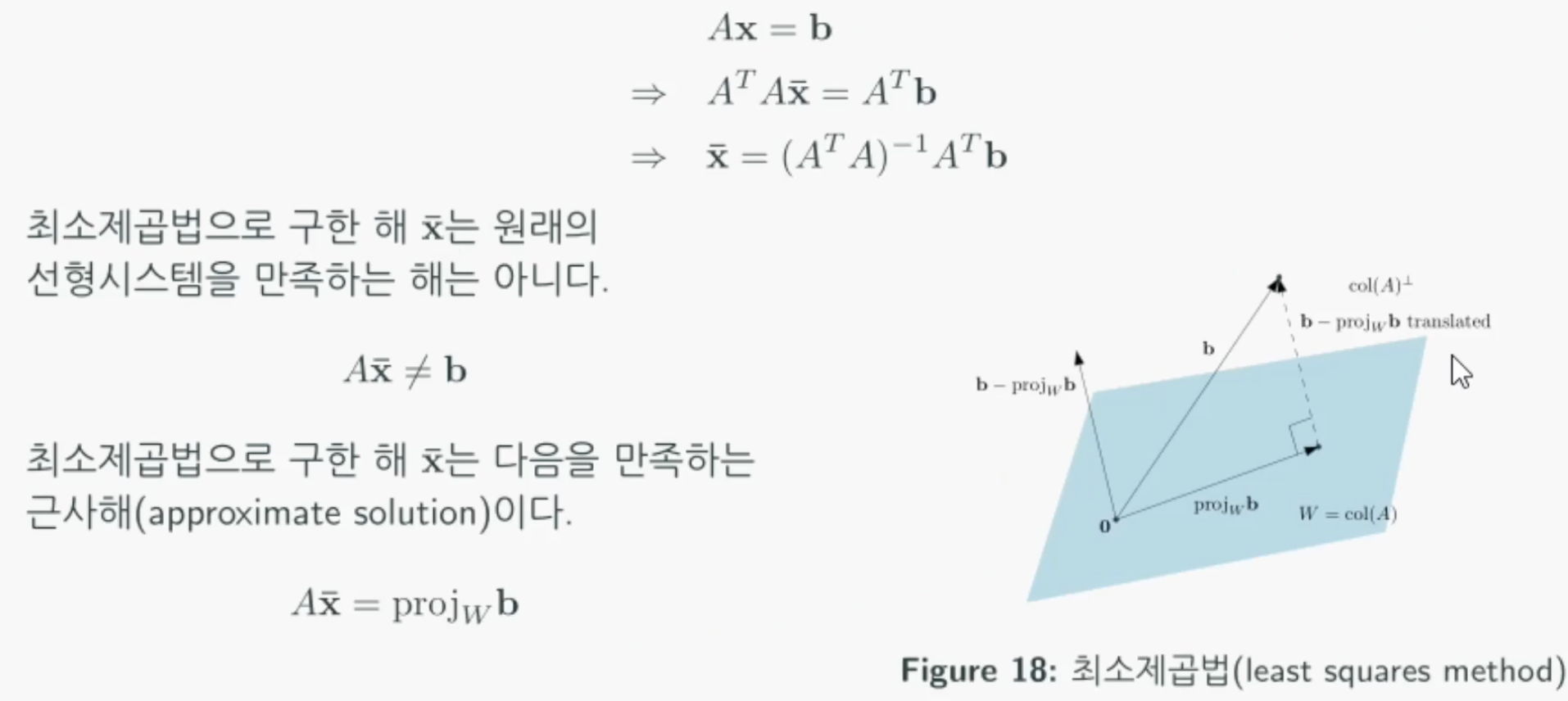
• Ax = b의 선형시스템에서 양변에 A의 전치행렬을 곱하면 최소제곱법의 해를 구할 수 있다.
  

선형회귀(Linear Regression)

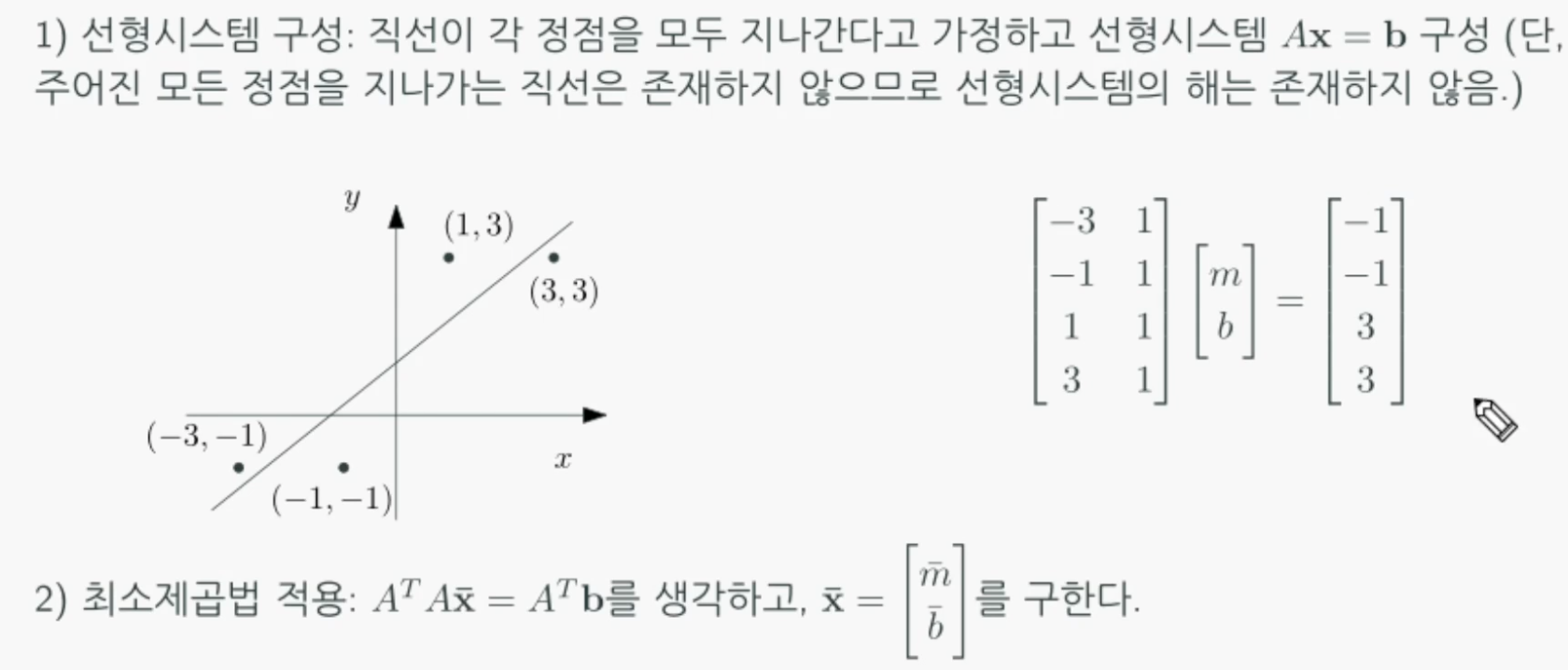
• 예를들어 어떤 데이터들이 2차원 공간에 분포해있을 때 그 데이터를 모두만족하는 직선이 없는 경우가 있다. 그 때 위에서 학습한 최소제곱법을 이용해 데이터들을 최대한 만족하는 직선을 구할 수 있는데 이를 선형회귀문제라고한다.
  

통계학(Statistics)

통계학이란?

• 데이터 수집, 구성, 분석, 해석, 표현 등에 관한 학문
• 기술통계학(descriptive statictics) : 수집된 데이터를 설명하는 분야
• 추출통계학(inferential statistics) : 수집된 데이터를 분석하고 추론하는 분야

모집단(population)

• 어떤 질문이나 실험을 위해 관심의 대상이 되는 개체나 사건의 집합

모수(parameter)

• 모집단의 수치적 특성

표본(sample)

• 모집단에서 선택된 개체나 사건의 집합

도수(frequency)

• 어떤 사건이 실험이나 관찰로부터 발생한 횟수
• 표현방법 : 도수분포표, 막대그래프(질적자료, 순서의미없음), 히스토그램(양적자료, 순서중요)
• 상대도수 : 도수를 전체 개수로 나눈 것

중앙값(median)

• 평균과달리 극단값의 영향을 받지않는다.
• 자료를 순서대로 나열했을 때 중간에 있는 값

분산(variance)

• 편차(값과 평균차이)의 제곱의 합을 자료의 수로 나눈 값
• 분산이 클수록 평균에서 값들이 멀리 떨어져있다고 볼 수 있다.
  

표준편차(standard deviation)

• 분산의 양의 제곱급
  

코드로 표현

## 둘중 아무거나 사용가능
import statistics
import numpy

a =[1,2,3,4,5,115]

print('mean:', statistics.mean(a))
print('median:', statistics.median(a))
## 표본분산
print('var:', statistics.variance(a))
print('var':, numpy.var(a))
## 모표본분산
print('pvar:', statistics.pvariance(a))
print('var':, numpy.var(a, ddof=1))
## 표본 표준편차
print('std:', statistics.stdev(a))
print('std':, numpy.std(a, ddof=1))
## 모 표준편차
print('pstd:', statistics.pstdev(a))
print('std':, numpy.std(a))
## 범위(range)
## feature scaling에 사용한다. 
print(max(a) - min(a))
print(numpy.max(a) - numpy.min(a))
## 사분위수(quartile)
- 전체 자료를 정렬했을 때 1/4, 2/4, 3/4 위치에 있는 숫자
print(numpy.quantile(a, .25) ## 제1사분위수
print(numpy.quantile(a, .5) ## 제2사분위수
print(numpy.quantile(a, .75) ## 제3사분위수
print(numpy.quantile(a, .60) ## 전체값 중 60%에 해당하는 값
print(scipy.stats.zscore(a) ## 평균으로부터 몇 표준편차 떨어져 있는지
print(scipy.stats.zscore(a, ddof=1) ## 평균으로부터 몇 표본표준편차 떨어져 있는지

z-score

• 어떤 값이 평균으로부터 몇 표준편차 떨어져 있는지 의미