LCS 알고리즘이란
LCS (Longest Common Subsequence) 알고리즘은 두 문자열 내에 존재하는 최장 공통 부분 수열을 찾는 알고리즘을 말한다. 간혹 '최장 공통 문자열' (Longest Common Substring)을 뜻하기도 한다. 두 가지는 확실히 다르니 잘 구분해야 한다.

최장 공통 부분 수열
가령 ABCDGEF 라는 문자열과 BGAGEFE 라는 문자열이 있다고 했을 때, 공통 부분 수열은 부분수열이기 때문에 각 문자들을 뛰어넘을 수 있고, 두 문자열에 공통으로 존재하면서 가장 긴 부분 수열인 BGEF 를 찾는 것이다.
공통 부분 수열은 A, B, AG 등 여러 개가 있을 수 있으며, 최장 공통 부분 수열 역시 여러 개가 있을 수 있다.
최장 공통 문자열
최장 공통 부분수열과 가장 다른 차이점은 '연속해야 한다'는 것이다.
위의 예시였던 ABCDGEF 라는 문자열과 BGAGEFE 라는 문자열에서 최장 공통 부분 수열은 BGEF 였지만, 이는 연속하지 않기 때문에 최장 공통 문자열은 될 수가 없다. 최장 공통 문자열은 연속하는 GEF 이다.
공통 부분수열과 공통 문자열의 공통적인 특징은 꼭 같은 자리가 아니어도 된다는 점이다. ABCDEF 라는 문자열과 CDEZXCV 라는 문자열이 있을 때 CDE 라는 공통 문자열은 첫 번째 문자열에서는 3~5번째에 위치하고 있고 두 번째 문자열에서는 1~3번째에 위치하고 있다. 이렇게 서로 위치가 달라도 공통으로 존재하기만 하면 상관이 없다는 특징이 있다.
최장 공통 문자열
최장 공통 부분 수열을 알아보기에 앞서 최장 공통 문자열을 구하는 방법을 알아보자.
먼저 두 문자열 A, B의 길이를 a, b 라고 하고 (a+1) * (b+1) 크기의 2차원 배열 LCS를 만든다. 크기를 1씩 크게 할당하는 이유는 계산의 편의를 위함이다. LCS 배열의 1행, 1열은 모두 0으로 초기화해준다.
이후 최장 공통 문자열은 다음과 같은 과정을 거쳐 구한다.
- 두 문자열에서 각각 한 글자씩 비교하며 이 때의 두 배열의 글자를 가리키는 인덱스를 각각
i,j라 한다. - 두 글자가 같다면
LCS[i-1][j-1]값에서 +1한 값을LCS[i][j]에 표시 - 두 글자가 다르다면
0을LCS[i][j]에 표시
두 문자가 같을 때
현재 보고 있는 두 문자가 서로 같을 때는, 앞서 공통 문자열이 이어져 오고 있었다면 그 공통 문자열의 길이가 1 늘어나게 된다. 만약 보고 있는 문자가 서로 달라 공통 문자열이 이어지고 있지 않았다면, 두 문자가 곧 새로운 공통 문자열의 시작이므로 길이 1을 기록해 준다.
두 문자가 다를 때
공통 문자열은 연속해야 한다는 특징이 있으므로 두 문자가 다르다는 것은 앞서 공통 문자열이 이어져 오고 있었든 아니든 공통 문자열이 끊기게 된다는 것을 의미한다. 즉 공통 문자열의 길이를 표시하는 LCS 배열에는 0을 기록해 준다.
점화식
if i == 0 or j == 0:
LCS[i][j] = 0
elif A[i] == B[j]:
LCS[i][j] = LCS[i-1][j-1] + 1
else: # A[i] != B[j]
LCS[i][j] = 0그림으로 살펴보기
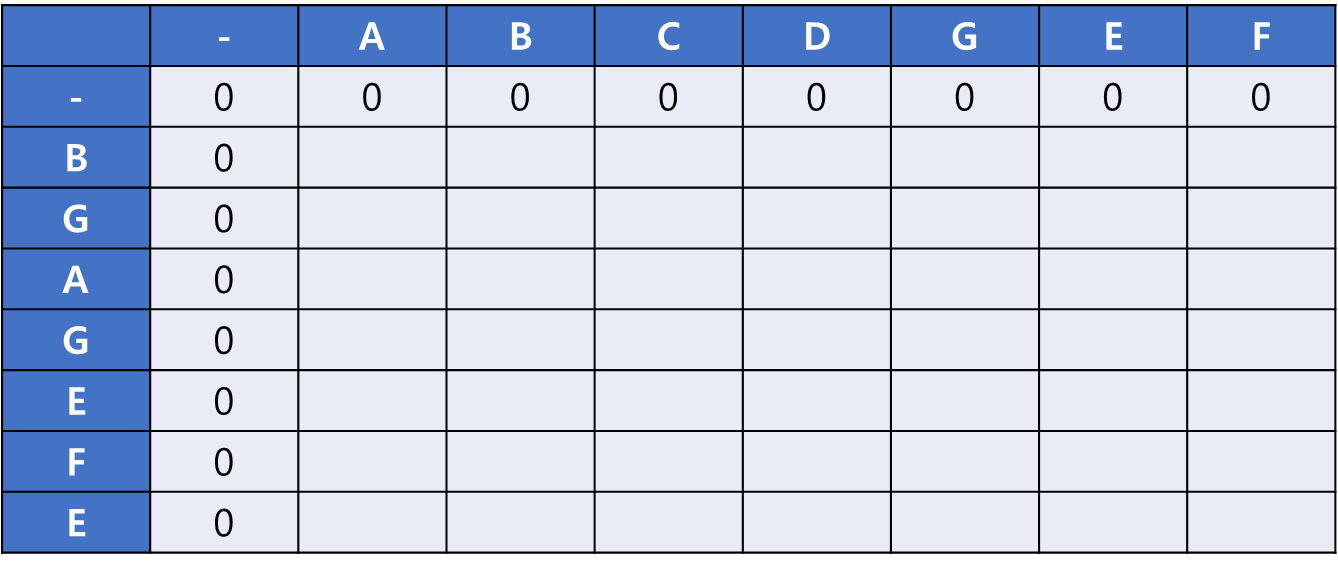
초기 상태이다. 문자열 길이보다 1씩 길게 할당해 주고 1행과 1열은 0으로 설정한다.
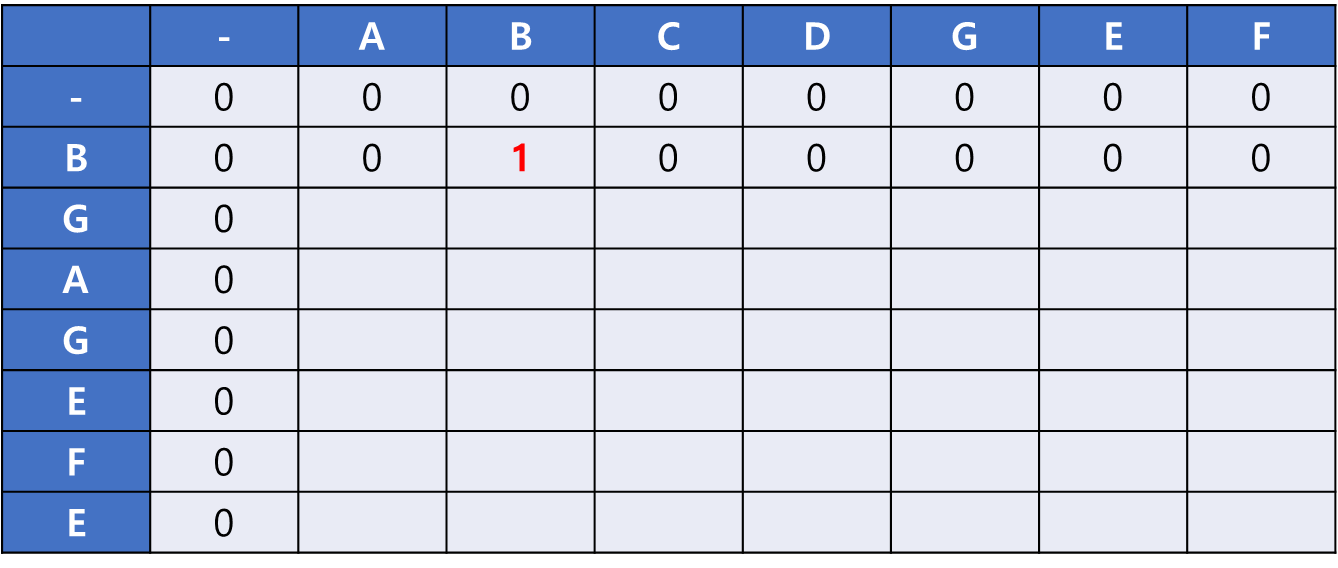
2행을 채운 뒤의 모습이다. 나머지는 모두 다르므로 0을, B 칸에는 좌측 상단 값에서 1을 증가시킨 1을 기록한다.
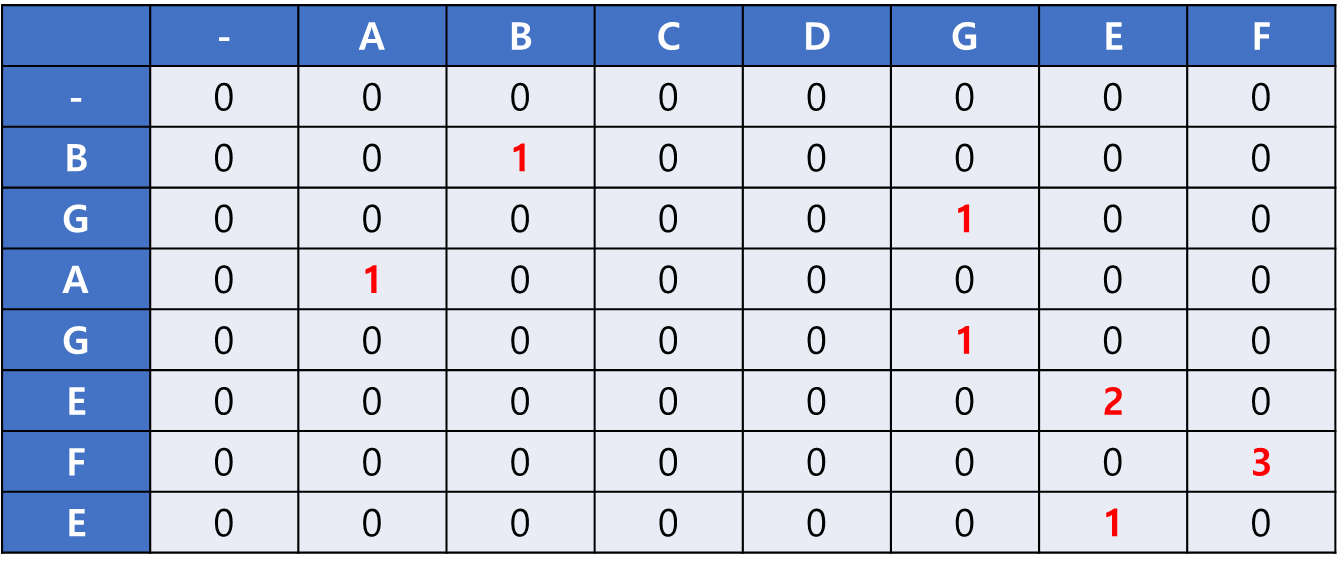
이를 반복하여 모든 2차원 배열을 채운다.
그리고 나면 표 안의 최댓값인 3이 최장 공통 문자열의 길이이다.
추가로 최장 공통 문자열을 찾고 싶다면 최댓값을 찾아 좌측 상단으로 거슬러 올라가기를 1을 만날 때까지 반복하면 된다.
최장 공통 부분수열
위에서도 알아보았듯 공통 부분수열은 공통 문자열과 다르게 연속하지 않아도 된다는 특징이 있다.
공통 문자열을 구할 때와 마찬가지로 두 문자열의 길이보다 1칸 크게 LCS 2차원 배열을 만들어 준다.
이후 공통 부분수열은 다음과 같이 구한다.
- 두 글자가 같다면
LCS[i-1][j-1]값에서 +1한 값을LCS[i][j]에 표시 - 두 글자가 다르다면
LCS[i-1][j]와LCS[i][j-1]중 큰 값을LCS[i][j]에 표시
두 문자가 같을 때
두 문자가 같으면 이전까지 구한 공통 부분수열의 길이를 늘일 수 있다.
두 문자를 확인하기 전까지의 최장 공통 부분수열의 길이는 LCS[i-1][j-1]에 이미 저장되어 있고, 이 값에서 1 증가한 LCS[i-1][j-1] + 1의 값을 LCS[i][j]에 기록한다.
두 문자가 다를 때
두 문자가 다르면 이전까지 구한 공통 부분수열의 길이는 늘일 수는 없지만, 공통 부분수열의 길이를 유지한 채 그대로 가져갈 수는 있다.
각각의 문자를 확인하기 이전까지 구한 공통 부분수열의 길이 LCS[i-1][j], LCS[i][j-1] 중 큰 값을 LCS[i][j]에 기록한다.
점화식
if i == 0 or j == 0:
LCS[i][j] = 0
elif A[i] == B[j]:
LCS[i][j] = LCS[i-1][j-1] + 1
else: # A[i] != B[j]
LCS[i][j] = max(LCS[i-1][j], LCS[i][j-1])그림으로 살펴보기
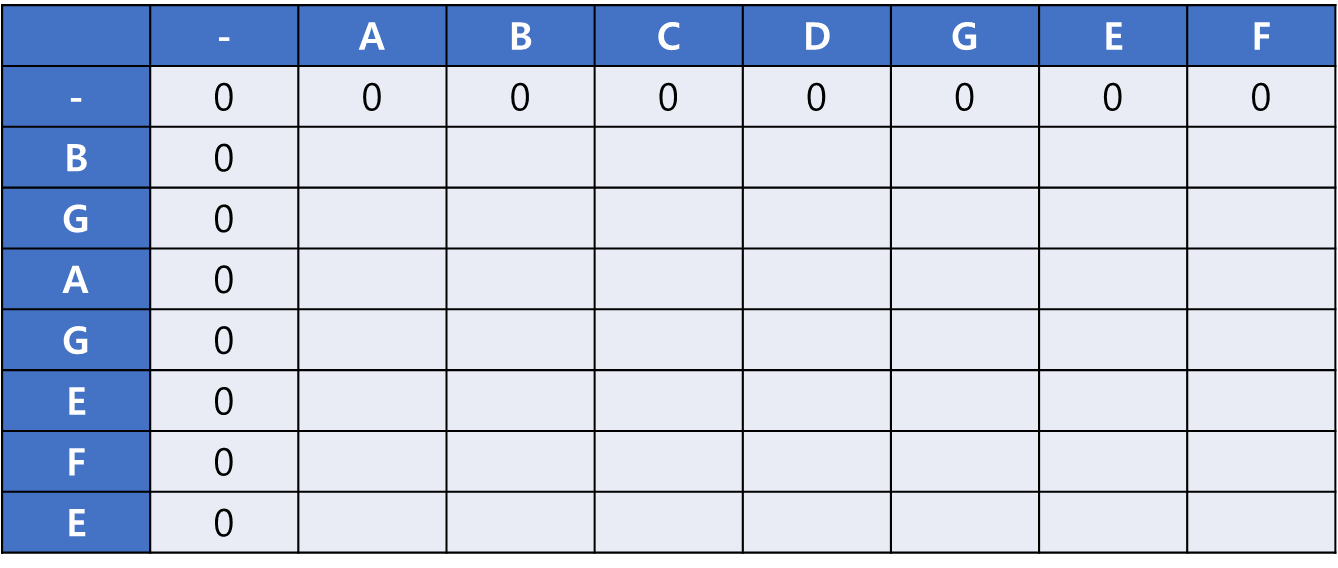
초기 상태 세팅은 공통 문자열을 구할 때와 동일하게 해 준다.
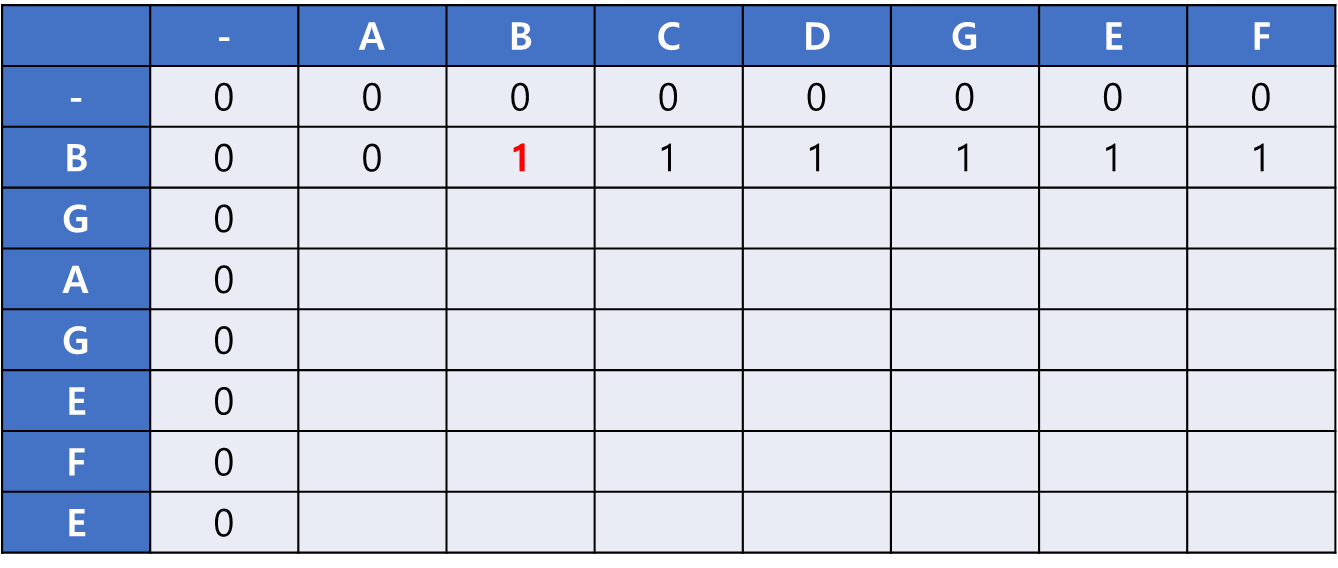
2행을 채워넣은 모습이다. B 칸에 1을 기록하였고, 그 뒤의 칸들에 대해서도 0과 1 중 큰 값인 1을 모두 채워넣었다.
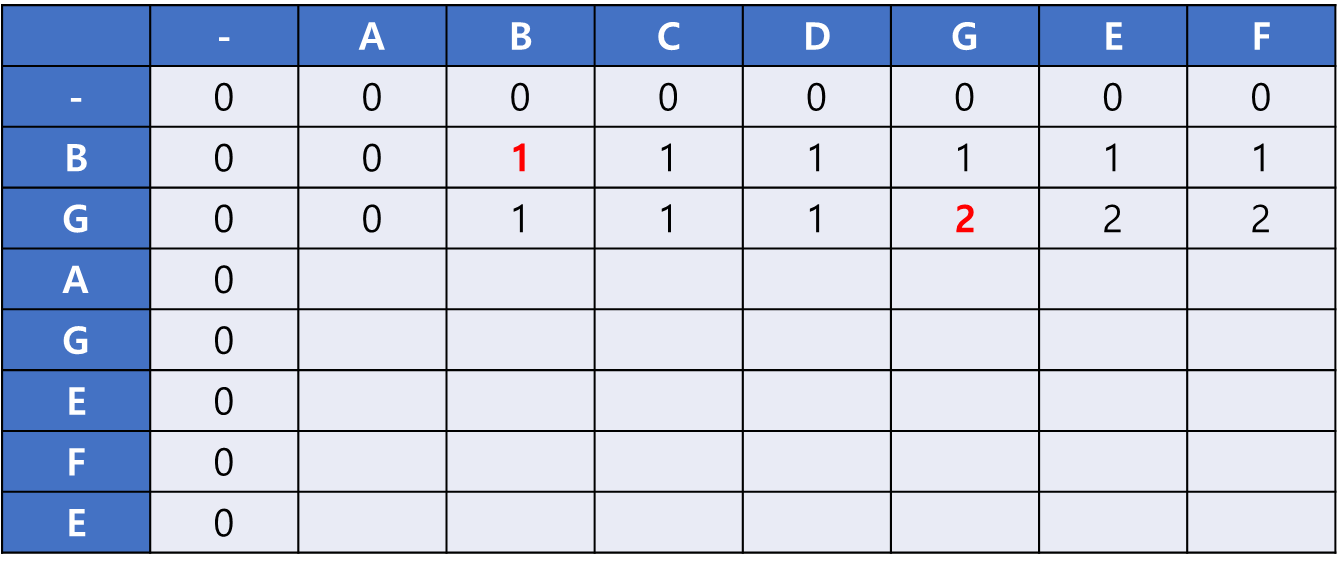
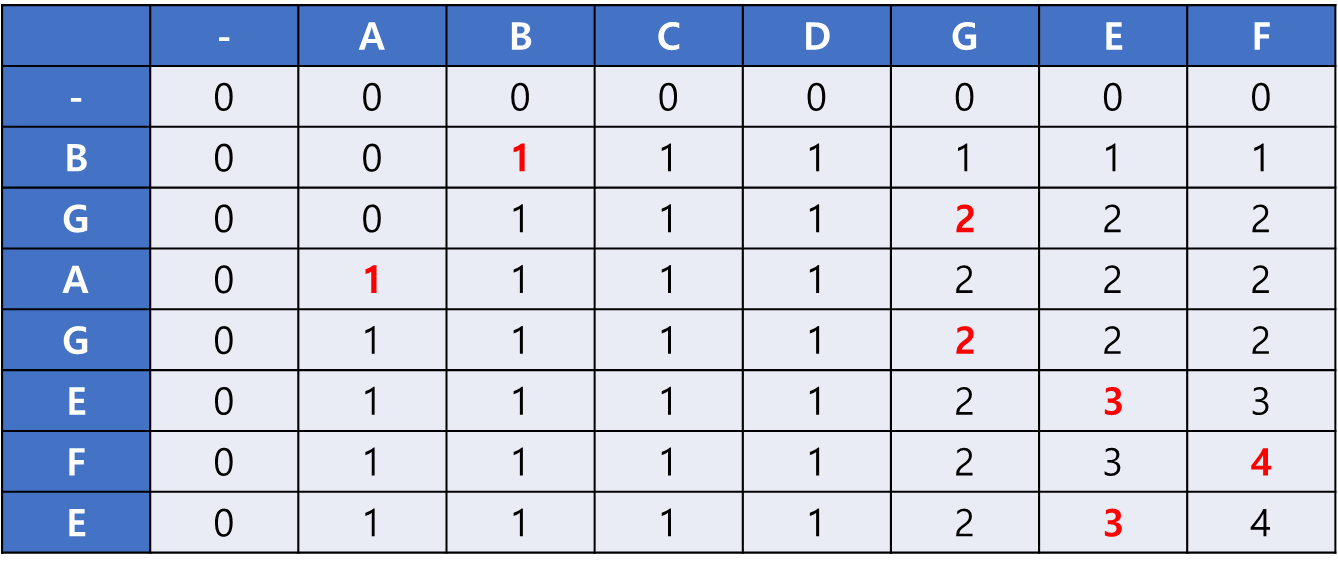
이후 점화식에 따라 계속해서 칸을 채워나간 모습이다.
그리고 나서 최댓값을 찾으면 최장 공통 부분수열의 길이를 구할 수 있다.
부분 수열 구하기
최장 공통 부분수열의 길이뿐만 아니라 수열 자체를 구하고 싶다면, LCS 배열을 거꾸로 역추적하는 방법으로 구할 수 있다.
시작은 마지막 칸에서부터 시작한다. 결과값을 담을 result 배열을 만들고, 다음과 같은 규칙을 적용한다.
LCS[i-1][j]와LCS[i][j-1]을 확인하고 현재 칸과 같은 칸이 있으면 그 칸으로 이동한다. (위를 먼저 탐색하는 것으로 가정)- 현재 칸과 같은 칸이 있으면
LCS[i][j]에 해당하는 문자를result배열에 넣고LCS[i-1][j-1]로 이동한다.
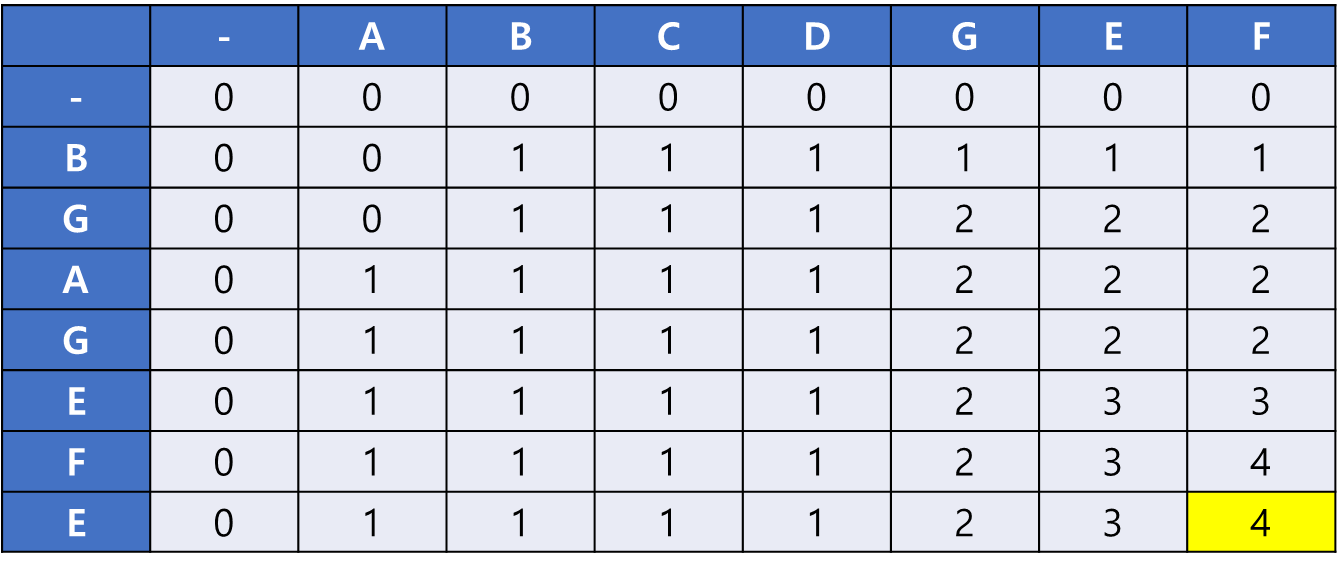
위쪽에 같은 값인 4가 있으므로 이동한다.
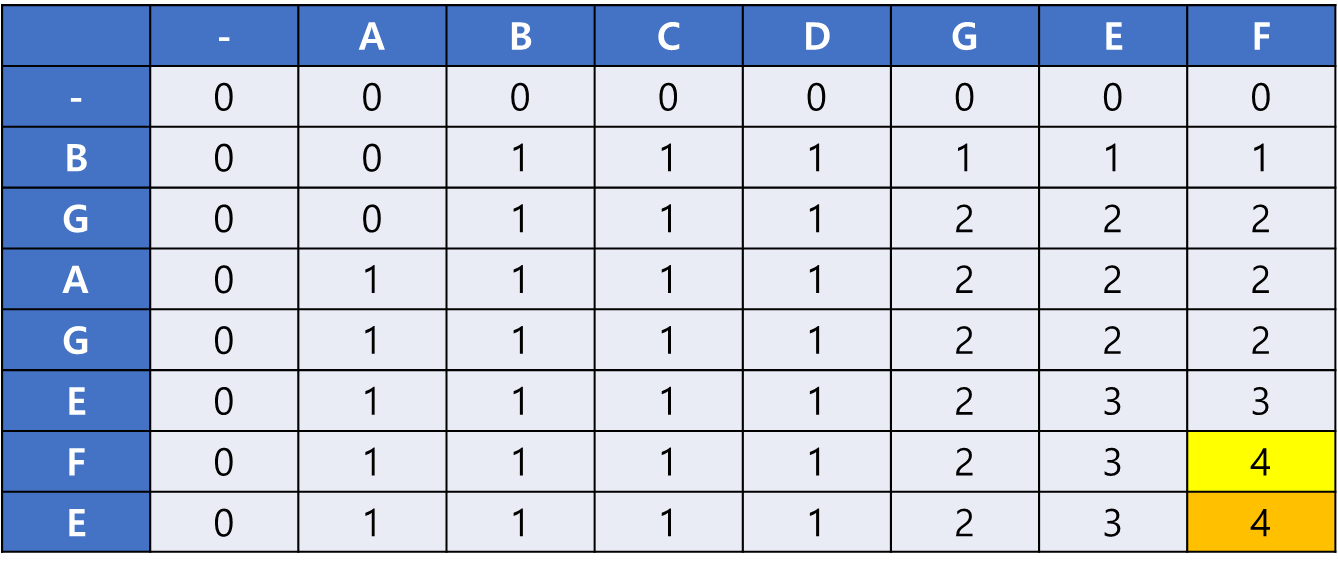
위쪽과 왼쪽에 4가 없으므로 result 배열에 F를 저장하고 LCS[i-1][j-1]로 이동한다.
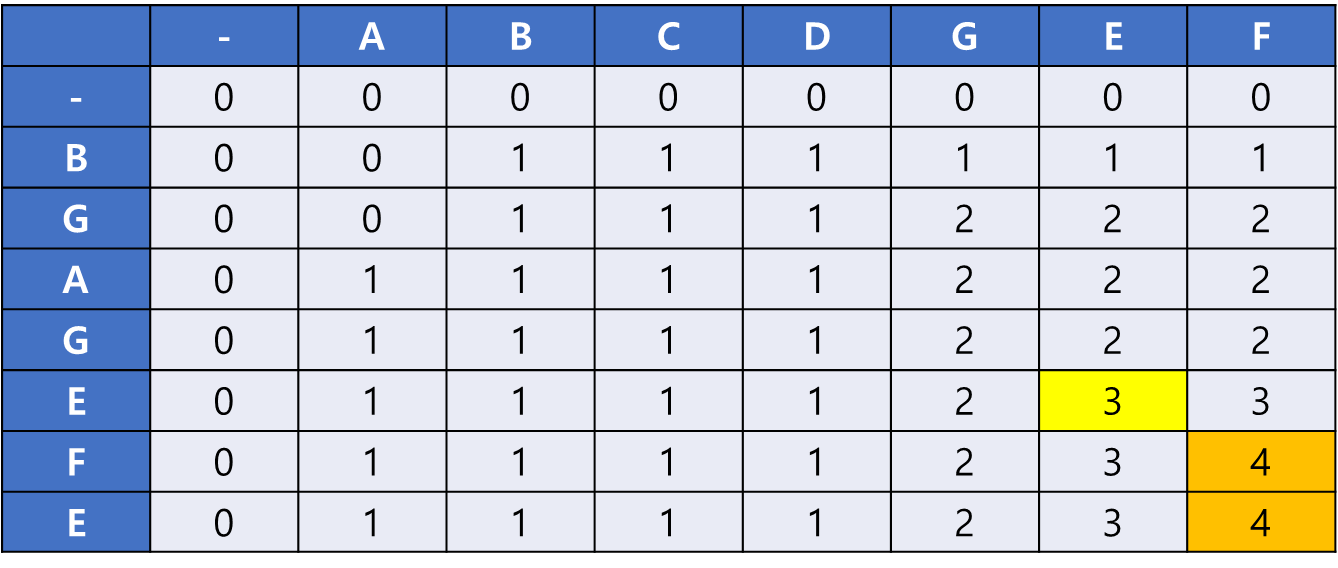
마찬가지로 위쪽과 왼쪽에 3이 없으므로 result 배열에 E를 추가하고 LCS[i-1][j-1]로 이동한다. result 배열은 현재 [F, E] 이다.
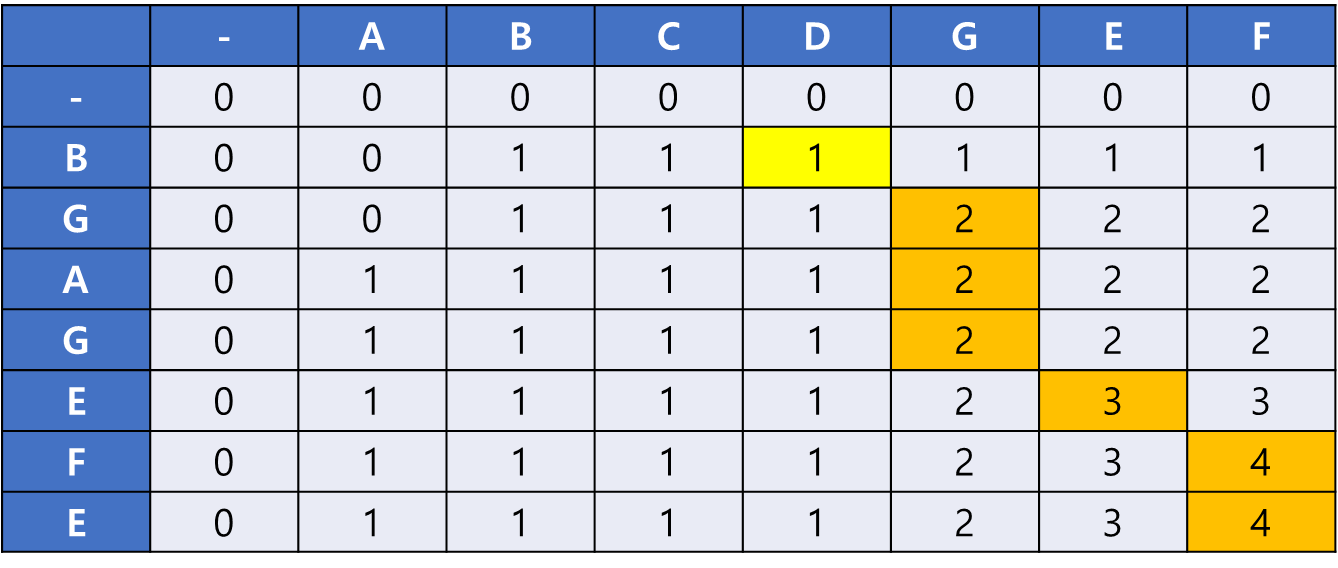
result 배열은 [F, E, G]
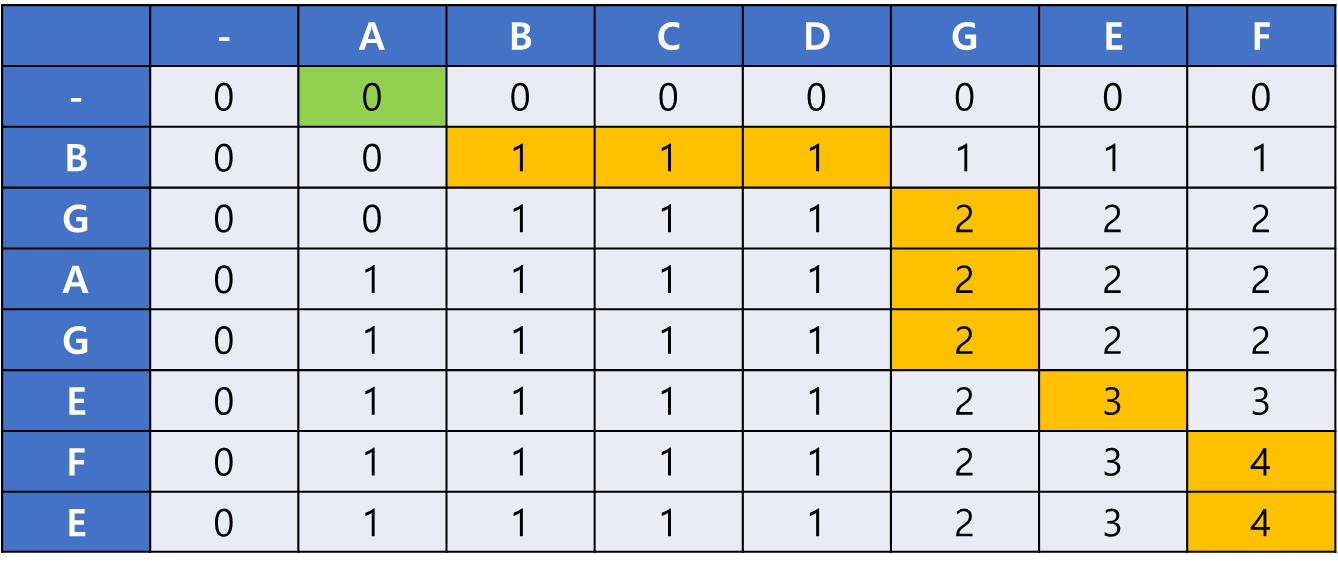
마지막 B를 result에 넣어주면 종료한다. (배열이 최장 부분수열의 길이, 그리고 0을 만났음) result 배열은 [F, E, G, B] 이다.
이제 이 result 배열을 뒤집어주면 최장 공통 부분수열을 구할 수 있다.
최장 공통 부분수열은 BGEF 이다.
같은 값을 만나 이동하는 과정에서 여러 갈래의 경우의 수가 있을 수 있는데, 결과적으로 모두 최장 공통 부분수열을 만들 수 있다. 두 문자열에서 최장 공통 부분수열은 여러 개가 있을 수 있다.
결론
최장 공통 부분수열(문자열) 알고리즘은 이전에 구해 놓은 값을 다음 번에 사용하는 동적 계획법 (Dynamic Programming)의 일종으로 자주 사용된다.

