⚠️ 이 글은 경북대학교 컴퓨터학부 이시형 교수님의 '알고리즘2' 수업을 수강하고 배운 점들을 복습하며 기록한 글입니다. 본문 내용을 비롯하여 사진 자료와 코드 또한 이시형 교수님의 수업자료에서 발췌하였습니다. 또한 모든 코드는 python을 사용합니다.

---

스택, 큐와 더불어 자주 쓰이는 자료구조인 우선순위 큐(Priority queue) 에 대해서 알아본다.

우선순위 큐란?

우선순위 큐는 큐와 유사하게 데이터를 추가하고 삭제하는 기능이 있는데, 큐에서는 가장 먼저 들어온 원소를 먼저 삭제(First in, First out, FIFO)인 반면 우선순위 큐는 가장 우선순위가 높은 원소를 먼저 삭제한다.

'우선순위' 란 사용자의 편의에 맞게 다양하게 정의할 수 있다. 가장 큰 원소일 수도 있고 가장 작은 원소일 수도 있고, 혹은 가중치가 가장 큰 원소일 수도 있다. 이 글에서는 가장 작은 원소를 먼저 제거하는 min priority queue를 다룬다.

따지고 보면 우선순위 큐는 큐와 스택을 모두 포괄할 수 있는 더 일반적인 개념이라고도 할 수 있다.

우선순위 큐 구현 방법

Unordered list

우선순위 큐를 구현하는 방법 중 첫 번째는 unordered list, 즉 정렬되지 않은 상태로 저장하는 방식이다.

삽입 insert

일반 큐와 마찬가지로, 단순히 큐의 맨 뒤에 붙이면 된다. 정렬되지 않은 상태로 저장하기 때문에, 위치를 고려할 필요가 없다.

뒤에 갖다붙이기만 하면 되므로 필요한 시간은 ~1 이다.

삭제 delMin

큐의 원소들 중 가장 작은 원소를 찾기 위해 전체 큐를 탐색해야 한다. 찾은 최솟값을 반환한다.

필요한 시간은 전체 큐를 탐색하므로 ~N 이다.

def insert(self, key):
    self.pq.append(key)

def delMin(self):
    minId, min = None, None
    for idx, item in enumerate(self.pq):
        if minId == None or item < min:
            minId, min = idx, item
    del self.pq[minId]
    return min

Ordered list

두 번째 방법은 큐 안의 원소들을 ordered, 정렬된 순서로 저장하는 방식이다.

삽입 insert

이진 탐색 (binary search)를 이용하여 추가할 위치를 찾는 것은 logN 시간 만에 가능하지만, 그 뒤의 원소들을 한 칸씩 뒤로 밀어 주어야 하는데 그 비용이 N에 비례한다.

즉 필요한 시간은 ~N 이다.

삭제 delMin

가장 작은 원소는 큐의 맨 첫 번째 원소이다. 그냥 삭제하면 된다.
뒤에 있는 원소들을 한 칸씩 당길 필요는 없다.

필요한 시간은 ~1 이다.

---

정리하자면, ordered list와 unordered list는 각각 장단점이 명확히 존재한다. ordered list는 삽입은 느린 반면 삭제가 빠르고, unordered list는 삽입은 빠른 반면 삭제가 느리다.

insert와 delMin두 작업의 비용은 1과 N 인데, 이 두 작업의 비용을 모두 logN으로 낮춘 것이 바로 이어서 살펴볼 heap 구조이다.

binary heap

binary heap은 complete binary tree 이다. 다음의 두 가지 성질을 동시에 가진다.

• binary tree : 모든 노드의 자식이 2개
• complete tree : 가장 아래 level을 제외한 모든 level이 빈 곳 없이 가득 차 있으며 가장 아래 level은 왼쪽부터 차례로 채워짐

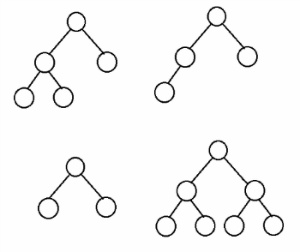
complete binary tree는 노드 수에 따라 유일한 모양을 가진다.

왜 tree를 사용하는 걸까??

각 level에 1개, 2개, 4개... n^k개의 노드가 존재하며, 그에 따라 전체 트리의 깊이는 logN (N: 노드의 개수) 이다.

그리고 complete binary tree의 경우, 왼쪽부터 차곡차곡 쌓이는 구조이므로 트리가 불균형하게 한 쪽으로 치우치거나 하는 일이 없어 깊이를 안정적으로 logN으로 유지할 수 있다.

complete binary tree의 또 하나의 장점은, 트리를 구성함에 있어 linked list가 아닌 1차원 배열에 담을 수 있어서 편리하다는 것이다.

배열에 담으면 부모-자식 간의 링크를 만들지 않아도 index만으로 찾아갈 수 있다.

node i의

• 부모 : i//2
• 왼쪽 자식 : i * 2
• 오른쪽 자식 : i * 2 + 1

그리고 index 접근의 편의를 위해 첫 노드(root노드)를 index 0이 아닌 index 1에 저장한다. 0번부터 저장하면 식이 더 복잡해진다.

heap order

가장 큰 원소를 우선 삭제하는 max PQ라고 가정하면, 부모 key >= 자식 key 관계를 유지함으로써 항상 가장 큰 원소가 index 1에 위치하도록 만들 수 있다.

heap order를 항상 만족하도록 저장하면 insert 작업과 delMax 작업을 모두 logN 시간 만에 수행 가능하다.

insert

heap에서의 insert는 다음의 세 가지 조건을 만족해야 한다.

• complete binary tree의 형태를 유지
• heap order 유지
• logN 시간만에

insert 하는 새 값을 k라고 할 때, 다음과 같은 과정을 거친다.

• k를 tree의 맨 마지막에 추가
• k를 부모 노드와 비교하여 만약 heap order를 어긴다면 (부모보다 큰 경우) swap 하는 것을 반복하며 부모 노드를 따라 계속 올라간다.(swim up) 만약 k보다 큰 부모를 만나면 그 위치가 k의 올바른 위치이다.

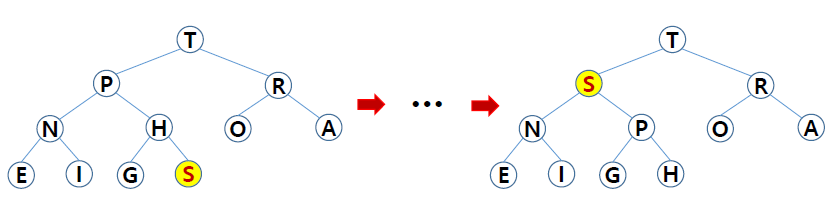
먼저 S를 트리 맨 끝에 붙이고, 부모와 비교를 시작한다. S는 H보다 크므로 H와 S 자리를 swap 해 주고, 다시 S와 그의 부모인 P를 비교한다. S는 P보다도 크므로 한 번 더 swap 해 준다. 즉 최종 트리의 구조는 오른쪽과 같다.

구현 코드

def insert(self, key):
    self.pq.append(key) # 맨 뒤에 append
    idx = len(self.pq) - 1 # append 한 key의 index
    while idx > 1 and self.pq[idx//2] < key: # pq[idx//2] (자신의 부모)와 비교해서 더 크면 swap
        self.pq[idx], self.pq[idx//2] = self.pq[idx//2], self.pq[idx] # swap
        idx = idx // 2 # 그리고 부모의 index로 수정(//2)함

---

• 트리의 맨 마지막 위치에 append 하고, 이를 부모와 swap 하는 과정을 거치므로 전체 트리의 구조는 insert 이후에도 complete binary tree이다.
• 새로 삽입한 노드와 그 부모들끼리만 swap 해 주어도 전체 트리는 heap order를 만족한다.
• 대소비교와 swap 하는 작업은 최대 트리의 깊이만큼만 수행되기 때문에 비용(시간) 역시 logN으로 제한된다.

delMax

heap에서의 delMax 또한 다음 세 가지 조건을 만족해야 한다.

• complete binary tree 형태를 유지
• heap order 유지
• logN 시간만에 삭제

트리의 최댓값을 삭제하는 delMax는 다음과 같이 구현한다.

• root 값 (가장 큰 값, 즉 삭제할 값)을 트리의 마지막 값과 swap, 삭제
• k를 자식 노드들 중 큰 쪽과 비교하여 heap-order를 만족할 때까지 swap 하는 것 반복 (sink)

즉 heap order를 만족할 때까지 자식 노드들 중 큰 쪽을 따라서 계속해서 내려간다.

root를 삭제한 후에 자식 중 더 큰 쪽을 swim up 시키면 되지 않는가??

-> 그러면 complete binary tree 모양이 깨질 수 있다.

더 큰 자식을 찾는 이유는??

-> 둘 중에 더 작은 자식을 올리게 되면, 부모보다 자식이 더 커지게 되어 heap order가 깨지게 된다.

---

• 기존의 모양을 유지한 채 마지막 노드만 삭제하고, sink 하는 과정도 노드끼리의 swap만 일어나므로 전체 트리 모양에는 변화가 없다. 즉 delMax를 수행해도 complete binary tree 구조를 유지할 수 있다.
• sink 해가는 과정에서 두 자식 중 큰 값과 swap 하므로 나머지 자식과의 대소 관계가 깨지지 않는다. 즉 전체 트리의 heap order도 깨지지 않않고 유지된다.
• insert와 마찬가지로, 전체 트리 깊이가 logN으로 제한되므로 비용(시간) 역시 logN 으로 제한된다.

우선순위 큐를 사용하는 예시

vs 정렬

입력이 실시간으로 들어오는 상황이라면 정렬 대신 PQ를 사용하는 것이 더 효과적이다. PQ는 어떤 값을 추가할 때 logN의 시간이 필요하지만 정렬의 경우 그 원소 이후의 원소들을 한 칸씩 밀어주어야 하므로 N의 시간이 걸리기 때문이다.

반대로 정렬을 사용해도 되는 상황에는 PQ를 사용해도 큰 문제는 없다.
정렬하는 데 NlogN 시간이 걸린다면. PQ를 사용해도 logN 작업을 N회 수행하므로 시간 소요는 비슷하다.

A* Search

어떤 목표를 향해 시행착오를 거치며 탐색한다고 할 때, 목표 상태와 비교적 가까운 상태가 있을 것이다. 그러한 상태는 목표 상태에 도달할 가능성이 더 높다고 보고 우선적으로 계속하여 탐색한다.
이 때 각 상태를 PQ에 넣어두고 그때그때 가장 탐색할 가치가 있는 상태를 PQ에서 꺼내 탐색한다면 보다 효과적으로 목표 상태에 도달할 수 있다.