⚠️ 이 글은 경북대학교 컴퓨터학부 이시형 교수님의 '알고리즘2' 수업을 수강하고 배운 점들을 복습하며 기록한 글입니다. 본문 내용을 비롯하여 사진 자료와 코드 또한 이시형 교수님의 수업자료에서 발췌하였습니다. 또한 모든 코드는 python을 사용합니다.

---

먼저 임의의 데이터가 주어졌을 때, 이를 순서대로 정렬하는 기본 방법 두 가지를 살펴본다.

Selection Sort

Iteration i 때 a[i] ~ a[N-1] 중 최솟값을 a[i]와 swap

• 0부터 N-1까지 N개의 데이터가 저장되어 있을 때, 가장 작은 원소를 찾아 가장 왼쪽으로 보내는 것을 반복
• iteration i 일 때 a[i] ~ a[N-1] 중 가장 작은 원소를 찾는다.
• 그리고 가장 작은 원소를 a[i]와 swap 하여, a[i] ~ a[N-1] 중 가장 작은 원소를 i 번째 자리에 오게끔 한다.

코드

def selectionSort(a):
    for i in range(len(a)-1):
        # find the minimum in a[i] ~ a[N-1]
        min_idx = i
        for j in range(i+1, len(a)):
            if a[j] < a[min_idx]:
                min_idx = j
        
        # swap the found minimum with a[i]
        a[i], a[min_idx] = a[min_idx], a[i]

성능

Selection Sort의 각각의 iteration i에서는 N-1-i번의 대소 비교가 이루어지고 한 번의 swap이 이루어진다.

이러한 iteration이 i가 0부터 N-2까지 진행되므로, 비교 횟수는 ~N^2/2가 된다.

또한, 위 비교 횟수는 입력 데이터에 따라 변하지 않는다. 예를 들어 입력이 이미 완전히, 혹은 거의 정렬된 상태로 들어오더라도 iteration i는 a[i] ~ a[N-1]을 모두 비교하여 swap 한다.

Selection Sort는 입력 데이터의 상태에 상관없이 ~N^2번의 대소비교가 이루어진다. (정렬된 데이터든 아니든)

Insertion Sort

Iteration i 때 a[i]를 왼쪽의 원소와 swap해 감. 그보다 크지 않은 원소가 나오면 STOP

• 0부터 N-1까지 N개의 원소가 저장되어 있을 때, a[i]의 올바른 위치를 찾아주는 것을 반복
• a[i]를 왼쪽의 원소와 하나씩 차례로 비교해 감
• a[i]보다 크지 않은 원소가 나오면, 그 자리에서 멈춤 (그 자리가 올바른 a[i]의 자리)

코드

def insertionSort(a):
    for i in range(1, len(a)):
        # element to move at current iteration
        key = a[i]

        j = i-1
        while j >= 0 and a[j] > key:
            # move element a[j] to a[j+1]
            a[j+1] = a[j]
            j -= 1

        # place the key to the farthest it can go to the left
        a[j+1] = key

• j = i-1에서부터 시작하여 a[j]가 key보다 크면 한 칸씩 오른쪽으로 민다.
• while loop을 빠져나왔을 때 j는 key보다 작거나 같은 값이 최초로 등장한 위치를 가리키고 있고, 그 위치 바로 다음 칸이 key의 위치이므로 a[j+1] 위치에 key를 삽입한다.

a[j]가 한 칸씩 오른쪽으로 밀리는 과정에서 a[i]의 값이 소실될 수 있으므로 key라는 별도의 변수에 저장해 두었다가 삽입한다.

성능

Insertion Sort는 입력이 거의 정렬되어 들어오는 경우가 많다면 N에 비례한 횟수의 비교/swap만 수행하므로 다른 정렬 방법보다 유리하다.

Selection Sort와는 다르게 Insertion Sort는 입력 데이터의 상태에 따라 성능이 바뀐다.

만약 완전 정렬된 데이터가 입력으로 들어왔다고 가정하면 iteration i에서 첫 번째 a[j] 즉 a[i-1]와 한 번만 대소비교를 하고 swap할 필요가 없다고 판단하게 되므로, 각 iteration당 1번의 대소비교만 이루어진다.

만약 worst case로 역방향으로 정렬된 데이터가 들어올 경우 iteration i에서 a[i] 왼쪽에 있는 원소 개수만큼 대소비교가 이루어지므로 약 N^2/2회 비교가 이루어지고 swap도 같은 횟수만큼 이루어진다.

평균적으로는 worst case의 절반 정도인 ~N^2/4회 비교 및 swap이 이루어진다.

대소 관계 정의 시 지켜야 할 규칙

• Anti-symmetry : if a<=b and b<=a, then a==b
• Transitivity : if a<=b and b<=c, then a<=c
• Totality : for every pair of elements a and b, either a<b or a>b or a==b

---

H-Sort와 Shell Sort

h-sort의 등장 배경

Insertion Sort는 데이터의 상태에 따라 성능이 변한다고 하였다.
바로 옆의 데이터와 swap이 일어나는 조건은 앞에 있는 원소가 뒤의 원소보다 클 때, 즉 정렬 순서에 어긋날 때 이다.

즉 정렬 순서가 어긋나 있는 횟수만큼 swap이 이루어진다. 이렇게 정렬 순서가 어긋나 있는 쌍을 Inversion 이라고 하자.

Insertion Sort에서 한 번의 swap은 하나의 inversion을 해결한다.
H-sort는 다음과 같은 물음에서 등장했다.

한 swap이 여러 inversion을 한 번에 해결하게 할 수 없을까?

정의

h-sort : 모든 h만큼 떨어진 원소끼리 insertion sort를 수행

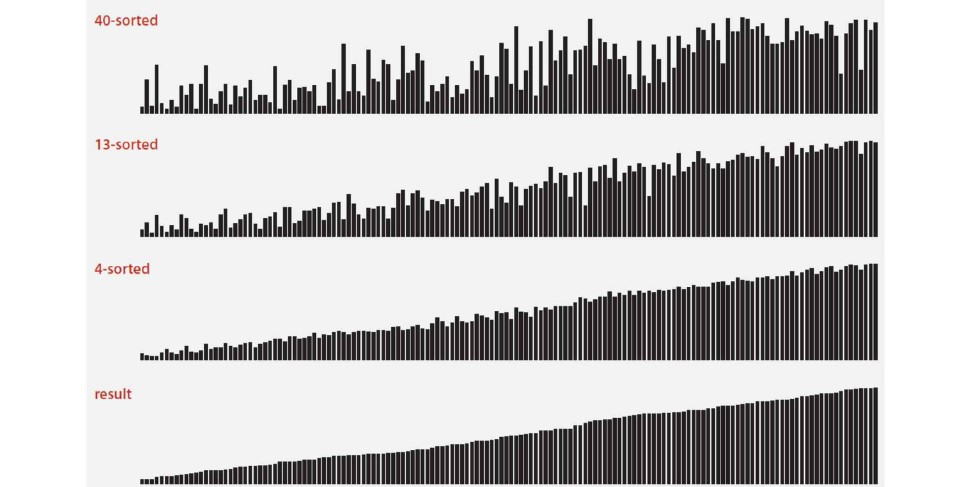
위 그림과 같이 바로 옆이 아니라 h만큼 떨어진 원소들끼리 대소비교를 하여 한 번에 여러 칸을 뛰어넘을 수 있게 한다.

h가 1이 아닌 이상 완전 정렬된 상태는 아니지만, 대략적으로는 정렬이 된다.

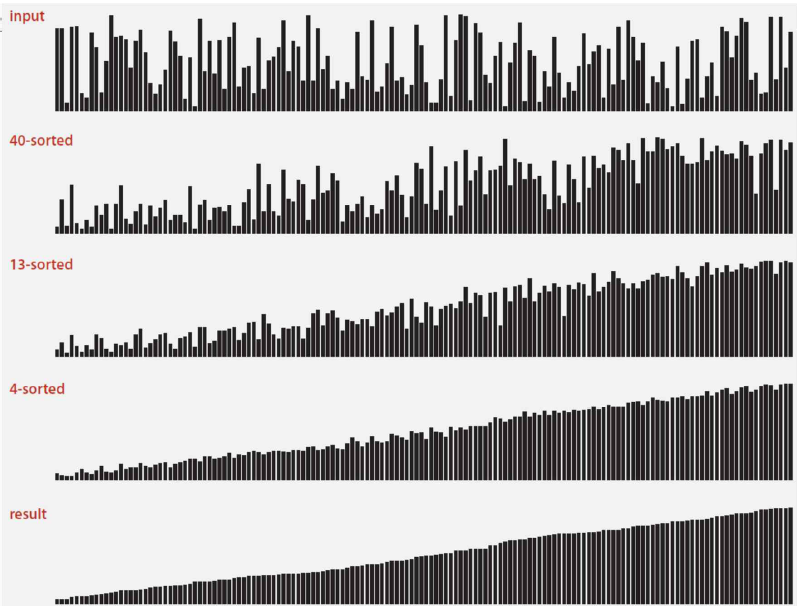
h의 값이 작아질수록 더 가까운 원소들의 세밀한 대소비교가 가능하므로 점점 더 정렬된 상태에 가까워진다.

그리고 h-sort에서 h가 1이면 우리가 기존에 알던 Insertion sort와 동일하다.

코드

def insertionSort(a):
    for i in range(1, len(a)):
        key = a[i]

        j = i-1
        while j >= 0 and a[j] > key:
            a[j+1] = a[j]
            j -= 1

        a[j+1] = key

def hInsertionSort(a):
	for i in range(h, len(a)):
    	key = a[i]
        
        j = i-h
        while j >= 0 and a[j] > key:
        	a[j+h] = a[j]
            j -= h
            
        a[j+h] = key

insertion sort도 결국 h-sort에서 h가 1인 케이스이므로 h-sort로 일반화할 수 있다.

모든 1 자리에 h를 넣어주면 된다.

---

Shell Sort

h를 점진적으로 1까지 감소시켜가며 h-sort를 수행함.
여러 칸을 앞으로 가야 할 것들을 한 번에 h칸씩 이동시킴으로써 비교/swap 횟수를 줄이는 방법이다.

h는 1씩 감소시키지 않고 더 큰 폭으로 감소시킨다.

여러 번 Insertion Sort 해도 괜찮나?

h가 1이 아닌 h-sort는 여러 칸 떨어진 원소끼리만 비교하므로 비교 횟수가 적고, 최종적으로 수행하는 1-sort는 앞의 h-sort들에 의해 거의 정렬된 상태이므로 ~N에 가까운 비교/swap 만으로 수행 가능하다.

h 값의 선정 기준은?

어떤 h 값을 가지고 h-sort를 수행하는 것이 최적인지는 아직 밝혀지지 않았으나 1, 2, 4, 8... 등의 2^k 수열은 짝수 번째와 홀수 번째 인덱스가 정렬되지 않으므로 사용할 수 없다.

그리고 Shell Sort의 성능 역시 아직 수학적 모델을 정확히 찾지는 못했다. h = 3x+1를 사용하는 경우 ~logN 회의 h-sort를 수행, 즉 NlogN 회의 비교/swap을 수행할 것으로 예측된다.

---

Shuffle

셔플 : 카드놀이에서, 카드를 잘 섞어 포개지는 순서를 바꾸는 일.

입력 데이터의 순서를 임의로 섞는 것을 말한다.

Naive한 방법

모든 가능한 순열을 발생시킨 후 하나를 선정한다.
길이 N인 순열의 개수는 N!이므로 ~N!에 비례한 방법이다.

Knuth's Shuffle

iteration i 때 a[0] ~ a[i] 중 하나를 uniformly random하게 선택해 a[i]와 swap

※ uniformly random : 모든 확률이 일정

코드

import random

def knuthShuffle(a):
	for i in range(1, len(a)):
    	j = random.randInt(0, i)
        a[i], a[j] = a[j], a[i]