이 글은 경북대학교 컴퓨터학부 이시형 교수님의 '알고리즘2' 수업을 수강하고 배운 점들을 복습하며 기록한 글입니다. 본문 내용을 비롯하여 사진 자료와 코드 또한 이시형 교수님의 수업자료에서 발췌하였습니다. 또한 모든 코드는 python을 사용합니다.

Union-Find란

N개의 점이 주어지고, 각 점들을 잇는 간선들은 없는 상태에서 시작한다. 여기서 두 점을 연결하는 간선을 추가하는 명령과, 어떤 두 점이 서로 연결되어 있는 상태인지를 판별하는 명령을 효율적으로 설계하고자 한다.

용어 정리
union(a, b) : 점 a와 b를 간선으로 연결함
connected(a, b) : a와 b의 연결 상태 True/False로 응답 (즉 a와 b를 연결하는 경로가 존재하는지)

Union Find는 간선이 추가됨에 따라 연결 상태가 지속적으로 변화한다. 즉 이전에 했던 답을 재활용하기보다는 그때그때 다시 확인이 필요하다.

Union Find는 어디에 활용되는가?

두 점이 서로 연결되었는지(connectivity)를 확인하며 계속 간선을 추가해보는 상황에 사용한다.

• 컴퓨터망에서 두 장비가 서로 연결되었는지 확인
• 비행기 노선도가 주어졌을 때 임의의 두 지역이 서로 도달 가능한지 확인
• 픽셀로 이루어진 이미지에서 같은 물체를 구성하는 픽셀을 확인

그래프 전체가 미리 주어지고 그래프의 점이나 간선의 형태가 변하지 않는 정적인 상황에는 DFS, BFS 등의 다른 알고리즘을 사용한다.

또한 두 점 간의 연결 여부만 판단하는 것이 아니라 최단 경로 등을 찾아야 하는 경우 등에는 다익스트라 등의 또 다른 알고리즘이 사용된다.

그래프 연결 상태의 저장

union 또는 connected 연산을 수행하려면, 당연히 그래프의 연결 상태를 저장해야 한다. 이 때 어떤 자료구조에 저장할지 또한 고려해볼 문제 중 하나이다.

adjacency list

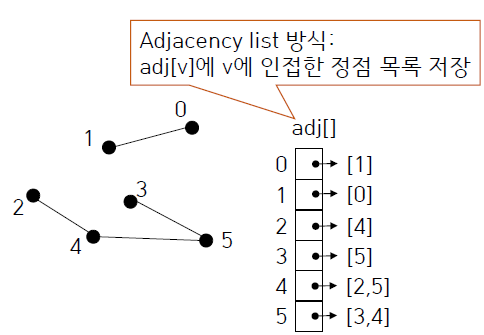
일반적으로 그래프 저장에 많이 사용되는 Adjacency List 방식 (adj[v]에 v에 인접한 정점 목록을 저장)을 생각해 볼 수 있다. Adjacency List 방식은 각 정점과 연결된 간선만을 표시하므로 NxN 배열보다 compact하다.

속도

Adjacency List 방식으로 간선 정보를 저장하고 union, connected 연산을 수행하면 그 속도는 어떠할까?

• union(a,b) : adj[a], adj[b]에 각각 b, a를 추가하면 되므로 상수 시간 (~1)
• connected(a, b) : adj[a]에 b가 있는지 탐색하면 되는데 worst case의 경우 E개의 간선이 모두 adj[a]에 포함될 수 있으므로 ~E

connected 연산이 다소 비효율적이다.

개별 간선 정보를 저장해야 하나?

두 점 간의 경로를 찾아야 하거나, 두 점을 직접 연결하는 간선의 존재 여부를 찾아야 하거나 등의 작업이 아닌, 단순히 두 점의 연결 여부만 판단하는 작업만을 고려할 때는 굳이 개별 간선 정보를 저장하지 않아도 충분해 보인다.

개별 간선 정보를 일일이 저장하지 않고도 그래프의 연결 상태를 표시할 수 있는 방법이 있을까?

Connected component

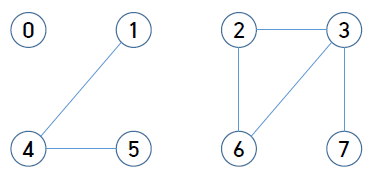
Connected component란 서로 연결된 정점들의 maximal한 집합이다.

서로 연결된 가장 큰 덩어리

위 그림의 경우 {0}, {1, 4, 5}, {2, 3, 6, 7} 총 3개의 connected component가 있다.

{4, 5}는 maximal하지 않기 때문에 connected component라고 할 수 없다.

위 그림에서 정점 2와 5를 연결하는 간선을 추가하면 서로 다른 두 connected component가 {1, 2, 3, 4, 5, 6, 7} 로 합쳐진다.

Quick Find

각 객체가 어느 connected component에 속하는지 크기 N의 배열에 기록 & 갱신

길이 N (정점의 개수) 배열 ids를 사용한다.
ids[i] : 객체 i가 속한 component의 id

component의 id란 서로 다른 component를 구분하기 위한 숫자이다. 즉 같은 component에 속하는 점들은 id가 같고 서로 다른 component에 속하는 점들은 id가 서로 다르다.

id를 정하는 방법은 여러 가지가 있겠으나, component에 속한 점 중 가장 작은 점의 번호를 사용하기로 한다.

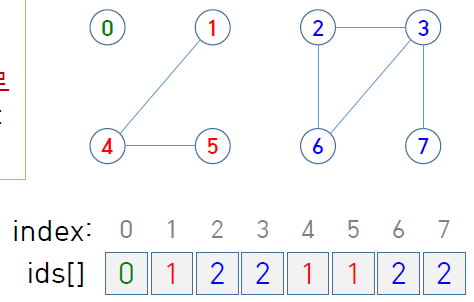
Quick Find를 사용하는 이유

• Quick Find는 각 정점의 id만 비교하면 되므로 connected 연산을 빠르게 수행할 수 있다.
• id 값만 확인하면 되므로 개별 간선의 정보를 일일이 저장하지 않아도 된다.

Quick Find의 구현 및 비효율적인 점

def connected(a, b):
	return ids[a] == ids[b]

def union(a, b):
	ids[i] == ids[b]인 모든 i에 대해 ids[i] = ids[a]로 값 교체
    또는
    ids[i] == ids[a]인 모든 i에 대해 ids[i] = ids[b]로 값 교체

두 개의 component A, B의 id가 각각 a, b이고 이 때 a>b 라고 가정하자.

그렇다면 union을 수행했을 때 component A에 해당하는 모든 정점의 id를 a에서 b로 수정해 주어야 한다.

이 과정의 비효율적인 점은 항상 N 크기의 배열을 선형 탐색 해야 한다는 점이다. 서로 union하는 component의 크기에 상관없이, 특정 id값을 가지는 정점을 탐색하기 위해서는 전체 배열을 탐색해야 하기 때문이다.

---

즉 Quick Find 기법의 경우 connected 명령은 상수 시간에 해결 가능하지만 union 명령은 정점 개수 N에 비례한 시간이 소요된다고 요약 가능하다.

Quick-Find의 다른 해석

connected component를 트리로 보는 관점

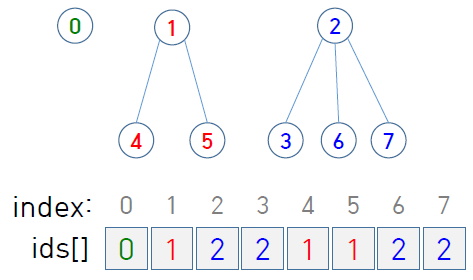
앞서 Quick Find에서는 connected component를 단순한 정점들의 연결 집합으로 보았다면, 부모-자식의 상하 관계가 있는 트리 구조로 볼 수도 있을 것이다. 즉 어떤 트리의 root 밑에 자식들이 달려 있는 구조이다.

그리고 ids[i]는 객체 i의 부모(parent)를 나타내기로 한다. 만약 i가 root라면 ids[i]=i이다.

또한 root(a) 라는 명령은 a가 속한 트리의 root를 반환하는 함수라고 정의한다.

def root(i):
	while ids[i] != i:
    	i = ids[i]
    return i

그렇다면 Quick Find의 union과 connected 명령을 다음과 같이 변경 가능하다.

• connected(p, q) : 두 정점 p, q가 각각 속한 tree의 root가 같은지 여부, 즉 root(p) == root(q)
• union(p, q) : p가 속한 tree 상의 모든 노드를 q가 속한 노드 아래로 옮겨 붙인다

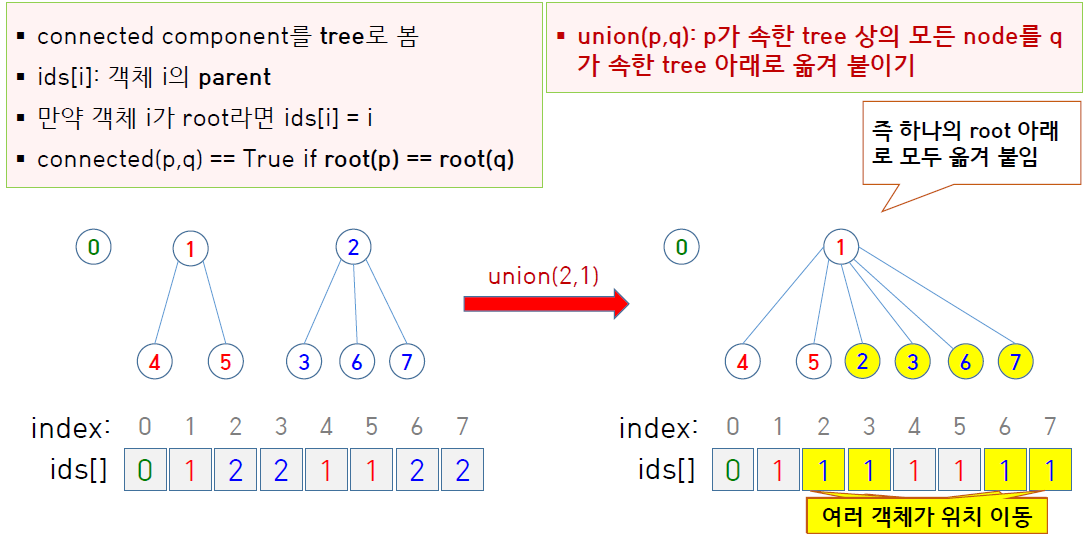
Quick-Union

위의 다른 해석을 개선한 것이 Quick-Union 기법이다.

union 할 때 모든 객체가 아닌 root만 옮겨 붙임으로써 속도 향상

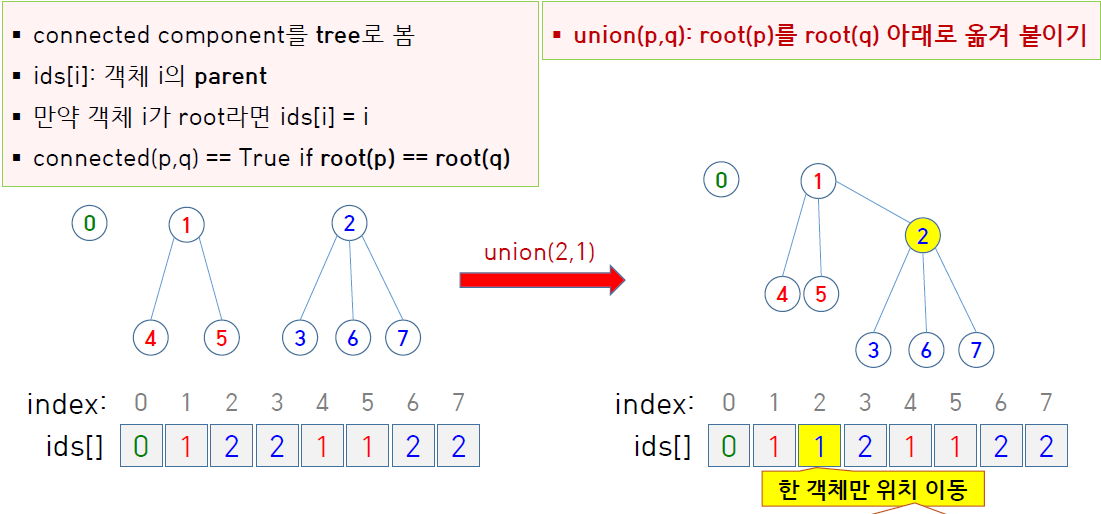
어떤 트리의 모든 정점을 다른 트리의 root에 이어 붙이지 않고 기존 트리의 구조를 유지하면서 한 트리의 root를 다른 트리의 root 밑에 이어 붙인다.

그러면 위의 그림에서 정점 3, 6, 7은 ids 값이 2인 채로 유지되는데, 여기서 어차피 2의 ids가 2에서 1로 변경되기 때문에 한 단계 더 거슬러 올라갈 뿐 결국 본인이 속한 트리의 root가 1이라는 사실을 알 수 있다는 것은 동일하다.

그렇다면 Quick-Union의 union과 connected 명령을 요약하면 다음과 같다.

• union(p, q) : root(p)를 root(q) 아래로 이어 붙이기.
  즉 ids[root(p)] = ids[root(q)]
• connected(p, q) : root(p)와 root(q)가 같은지 반환

Quick-Union 코드 정리

def root(i):
	while ids[i] != i:
    	i = ids[i]
    return i

def connected(p, q):
	return root(p) == root(q)

def union(p, q):
	ids[root(p)] = ids[root(q)]

Quick-Union의 성능

앞서 살펴본 Quick-Find의 경우 모든 정점의 id 값을 바꿔 주어야 하므로 union 함수에 for loop이 포함되어 있는 반면, Quick-Union의 경우 트리 구조 내에서의 부모-자식 상하 관계를 유지하며 root 노드 하나의 id 값만 변경하기 때문에 더 간단하다고 볼 수 있다.

union(a, b) 명령을 수행할 때 a의 root를 찾는 root(a)의 연산이 필수적인데, 이 때 root() 함수의 성능은 a가 속한 트리의 깊이에 비례한다. 단 worst-case의 경우 여전히 트리 탐색에 ~N에 해당하는 시간이 소요된다.

즉, 어느 한 노드가 속한 트리를 반대편 노드의 트리에 이어붙이는 과정에서 트리의 전체 깊이를 얕게 하는 방법을 강구할 필요가 있다.

Weighted QU

Weighted QU는 QU(Quick Union)에서 트리의 깊이를 제한하기 위한 방법이다.

앞서 Quick-Union, 한 노드가 속한 트리의 root 노드를 다른 노드가 속한 트리의 root 노드 아래에 이어 붙이는 방법을 살펴보았다.

이 방법의 worst case는 트리가 일직선 형태인 상황, 즉 트리의 깊이가 트리의 전체 노드 개수인 상황이다. 이러한 상황에서는 결국 root를 찾는 데 트리의 노드 개수 ~N 만큼의 시간이 소요되어 비효율적이다.

즉 트리를 좌우로 균형있게 이어 붙임으로써 트리의 전체 깊이를 최소화하는 방법을 알아보고자 한다.

Weighted QU의 원리

두 트리의 크기가 서로 다를 때, 작은 트리를 큰 트리 아래에 이어 붙이는 것이 전체 트리의 깊이를 덜 늘어나게 하는 방법일 것이다.

예를 들어 깊이가 3인 트리와 5인 트리가 있을 때, 5 트리를 3 트리 아래에 이어 붙이면 결국 전체 트리의 깊이는 6이 된다. (5인 트리 위에 root가 생겨서 +1)

그러나 3 트리를 5 트리 아래에 이어 붙여도 여전히 트리의 깊이는 5이다.

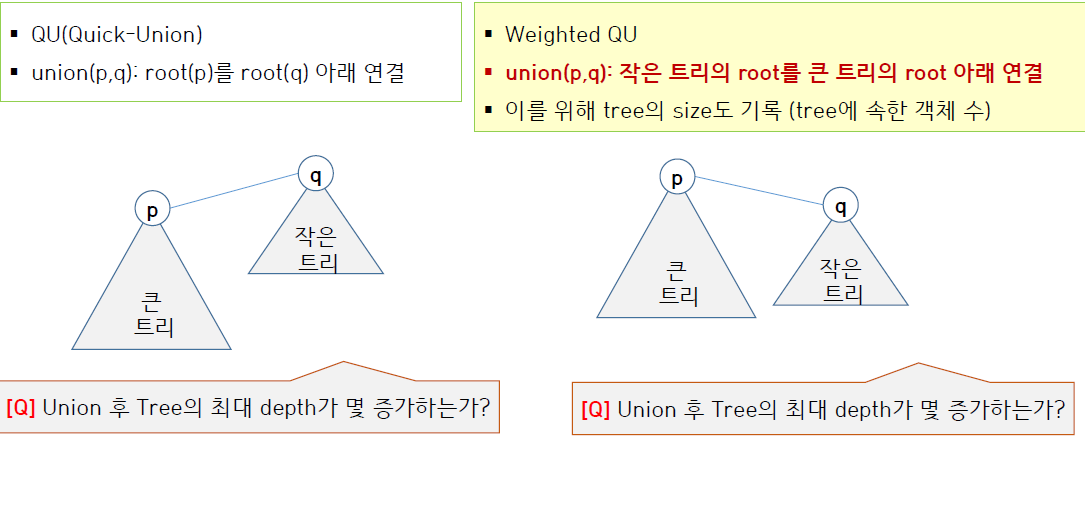
즉, 두 트리를 이어 붙일 때 작은 트리를 큰 트리 아래에 이어 붙이는 것이 좋다.

이렇게 작은 트리를 큰 트리 아래에 이어 붙일 때, 트리의 전체 깊이가 증가하는 경우는 두 트리의 깊이가 같을 때 일 것이다. (5 트리와 5 트리를 이어 붙이면 6 트리가 됨)

즉 우리는 두 트리 중 어떤 트리가 더 작고 큰지를 나타내기 위해 트리의 크기 또한 저장해야 한다. 이 때 트리의 크기 란 트리에 속한 정점 수이다.

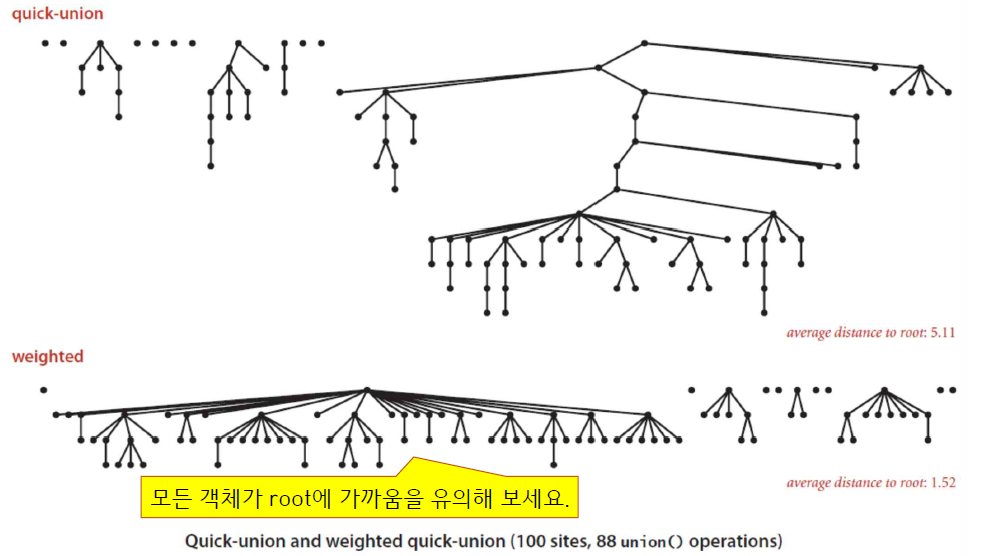
크기 비교를 하지 않고 마구잡이로 이어 붙였을 때에 비해 훨씬 더 트리의 전체 깊이가 얕아지는 것을 확인할 수 있다.

Weighted QU의 union

union(p, q)를 수행한다고 가정했을 때, 일단 p, q 각각이 어떤 트리에 속하는지를 파악해야 한다. 즉 root(p), root(q)를 수행하여 각 트리의 root를 찾는다.

이 때 root가 서로 같다면 이미 같은 component에 속한다는 뜻이고, cycle 방지를 위해 바로 return 한다.

그리고 size 배열의 root 인덱스를 참조하여 두 트리의 크기를 비교한다. 이 때 p가 속한 트리가 더 작다고 가정하면, id1을 root로 가지는 트리를 id2를 root로 가지는 트리 아래에 이어 붙이는 것이므로 ids[id1] = id2를 수행하고, 두 트리의 크기가 합쳐졌으므로 size[id2]에 size[id1]을 더해준다.

여기서 왜 size[id1]은 수정하지 않을까?
-> size 배열에 참조되는 인덱스는 각 트리의 root 뿐이다. 즉 root 이외의 인덱스 값은 접근할 일이 없다. id1 노드는 이제 id2 트리 아래에 속하게 되었으므로 더이상 root가 아니다. 즉 size[id1]에 더이상 접근할 일이 없으므로 굳이 수정하지 않는다.

def union(p, q):
	id1, id2 = root(p), root(q)
    if id1 == id2:
    	return
    
    if size[id1] <= size[id2]:
    	ids[id1] = id2
        size[id2] += size[id1]
    else:
    	size[id2] = id1
        size[id1] += size[id2]

Weighted QU의 최대 트리 깊이

Weighted QU 방법을 사용하면 N개 객체가 있다고 할 때 어떤 객체 x의 깊이도 log2N을 넘지 못한다.

증명

임의의 정점을 x라고 할 때, 자신이 속한 트리 내부에서의 x의 깊이가 1 늘어나는 경우는 x가 속한 트리가 다른 트리 밑에 붙을 때 이다. 다른 트리가 x가 속한 트리의 아래에 와서 붙을 때는 x의 깊이가 변하지 않는다.

그리고 이런 경우는 x가 속한 트리 크기가 더 작거나 같기 때문에 발생하며, 이 과정을 거칠 때마다 x가 속한 트리의 크기는 최소 2배 커진다. (두 트리 크기가 같을 때 2배 증가, 그 외에는 2배보다 많이 증가)

최대한 균형 있게 붙이기 때문에, 이런 식으로 깊이가 증가하는 경우는 최대 log2N 번이다.

그리고 x의 깊이가 k번 +1 된다고 가정하면 x가 속한 트리는 +1 될때마다 2배 이상씩 커지므로, x가 속한 트리의 크기는 최소 2^k이다.

이 때 전체 그래프에 N개 객체만 있으므로 2^k <= N이다.

즉 k <= log2N 이라고 할 수 있다.

Weighted QU의 성능

전체 그래프를 트리 형태로 표현하고, root를 찾아 root를 다른 root 아래에 이어 붙이는 매커니즘은 Quick-Union과 동일하다.

앞서 Quick-Union 방법을 살펴볼 때에도 트리의 깊이에 비례하는 성능을 가진다고 하였는데, Weighted QU 방법은 전체 트리의 깊이를 log2N으로 제한하는 방법이므로 union과 connected 모두 log2N 안에 수행 가능하다.

정리

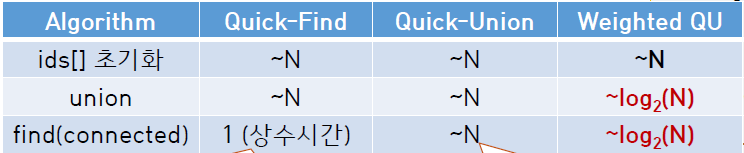
Quick Find

ids 배열 개념 도입

• union을 수행할 때마다 한 쪽의 id값을 가지는 모든 노드에 대해 다른 쪽의 id 값으로 수정해 주는 과정을 거치므로 ~N
• 그러나 connected는 ids 배열의 값만 확인하면 되므로 ~1

Quick Union

그래프를 트리 형태로 보는 관점 도입, root 개념 도입

• union을 수행할 때마다 한 정점이 속한 트리의 root를 다른 한 정점이 속한 트리의 root 아래 이어 붙임. 이 때 root를 찾는 과정인 root() 함수가 트리의 깊이에 비례한 시간 소요, 즉 worst case로 ~N

• connected 역시 root() 함수가 트리의 깊이에 비례한 시간이 소요되므로 ~N

Weighted Quick Union

그래프의 전체 깊이를 최소화하기 위해 그래프의 크기 개념, 대소비교 도입

• union을 수행할 때 두 트리의 크기를 비교해서 둘 중 작은 트리를 큰 트리 아래에 이어 붙임

즉 트리의 깊이가 얕아지고 즉 root() 함수가 개선됨. 곧 union과 connected 함수 또한 트리의 깊이, 즉 log2N 만에 수행 가능함