이전에 다익스트라 알고리즘을 visited 리스트와, 그때그때 최솟값을 찾아서 구하는 방식으로 구현해보았다. 이번에는 우선순위 큐, heapq를 이용해서 좀 더 시간적으로 효율적인 방법을 다룬다.
우선순위 큐? 힙?
큐 자료구조는 먼저 들어온 정보가 먼저 나가는 FIFO 자료구조인 반면, 우선순위 큐는 우선순위가 높은 정보가 먼저 나가는 자료구조이다.
우선순위 큐는 일반적으로 힙을 통해 구현한다.
힙은 완전 이진 트리 형태를 띠고 있는 자료구조이며, max heap과 min heap이 있다. 최솟값/최댓값 탐색이 빠르다는 이점이 있다.
다익스트라 알고리즘에 우선순위 큐 도입하기
다익스트라 알고리즘에서 출발 노드까지의 거리가 가장 짧은 노드가 우선순위가 가장 높을 것이다. 우선순위 큐 안에는 노드 A로 가는 여러 거리들이 들어갈 수 있는데, 자동으로 가장 최솟값을 찾아줄 수 있으므로 나머지 값들은 다 무시하면 된다.
진행 방식
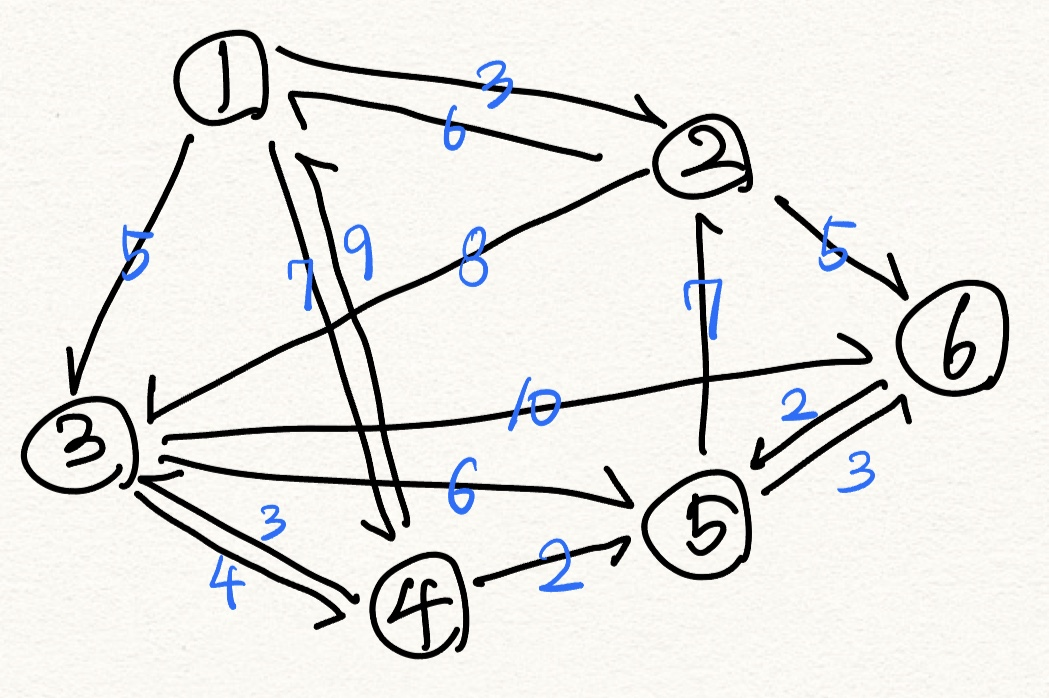
위와 같이 그래프가 있다.
이번에도 시작 노드는 1번으로 가정한다.

출발 노드부터 시작하여 해당 노드까지의 최단 거리를 저장하는 리스트를 만든다. 이 리스트를 'dist' 라고 하자. 지금은 초기 상태라서 모두 INF인데 출발지점은 1이니까 dist[1]에는 0이 들어간다.

그리고 (우선순위에 따라) 데이터들이 쌓이는 큐를 만든다.
맨 처음에 출발 노드와 출발 노드로부터 떨어진 거리 정보를 큐에 넣는다. (0, 1)이 큐에 들어간다. 우선순위 큐에 튜플을 넣을 경우 첫 번째 인자 기준으로 최솟값을 찾으므로, 거리 정보가 먼저 들어가야 한다.
그리고 큐에서 데이터를 뺀다. 지금은 값이 하나지만, 앞으로도 넣는 순서에 관계없이 항상 최소 거리의 정보가 나올 것이다. 직전에 넣은 (0, 1)이 빠져나왔다.
그럼 지금 내가 관심있는 기준 노드는 1이다. 이제 dist 리스트를 수정할 차례다.
수정하는 기준은 다음과 같다 :
A에서 갈 수 있는 각각의 노드 V에 대해,
내가 이전에 기록해둔출발지 -> 노드 V의 최단거리보다, 내가 방금 빼낸 노드 A에 대해출발지 ->(A까지의 최적 경로) -> 노드 A -> 노드 V의 거리가 더 짧을 때
여기서 출발지 -> 노드 V의 최단거리 는 dist[V] 일 것이고
출발지 -> 노드 A -> 노드 V의 최단거리 는 dist[A] + (A->V의 간선 비용) 일 것이다.
이와 같은 정책으로 거리 정보를 갱신하면 다음과 같다.

앞에 0+는 dist[1]의 값이다. (일반화해서 보기 편하게 처음부터 이렇게 표시한다)
그 다음, 수정된 사항에 대해서 우선순위 큐에 집어넣는다. 큐에는 (새로 갱신된 거리, 그 노드) 순서로 들어간다.

맨 앞에 최솟값이 있는 상태로 이런 식으로 들어갔다.
이제 다시 큐에서 데이터를 뺀다. (3, 2)가 빠져나왔다. 큐에는 (5, 3), (7, 4) 차례로 있다.
2번 노드에서는 1, 3, 6번 노드로 갈 수 있다.

마찬가지로 dist 리스트에 수정사항이 있는지 확인한다. 각각 보는 내용은 다음과 같다.
- dist[1] > dist[2] + (2->1 거리) ?
=0 > 3 + 3:수정 필요 없음 - dist[3] > dist[2] + (2->3 거리) ?
=5 > 3 + 8:수정 필요 없음 - dist[6] > dist[2] + (2->6 거리) ?
=INF > 3 + 5:수정 필요
6번 노드는 기존 dist 값이 INF였으므로 dist 값을 수정해 주자.

그리고 수정된 정보에 대해 큐에 넣는다. (8, 6)이 들어간 후 큐의 모습은 다음과 같다.
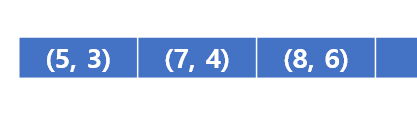
반복한다. (5, 3)을 빼고 3에서 갈 수 있는 노드들인 5, 6에 대해 검사한다.
- dist[5] > dist[3] + (3->5 거리)
=INF > 5 + 6:수정 필요 - dist[6] > dist[3] + (3->6 거리)
=8 > 5 + 10:수정 불필요
5번 노드는 기존 dist 값이 INF였다. 수정한다.

그리고 (11, 5)를 큐에 넣는다. 맨 뒤로 들어간다.
이런 식으로 큐가 다 소진될 때까지 진행하고 나면, dist 리스트에는 출발 노드(1)로부터 각 노드까지의 최단 거리가 들어가 있다.
구현
import heapq
import sys
input = sys.stdin.readline
v, e = map(int, input().split())
s = int(input())
INF = 9999999
dist = [INF] * (v+1) # 시작노드에서부터 v로 가는 최소 비용
graph = [[] for _ in range(v+1)] # [v1에서][v2, v2로 가는 비용]
for _ in range(e) :
v1, v2, cost = map(int, input().split())
graph[v1].append((v2, cost))
def dijkstra(start) :
q = []
heapq.heappush(q, (0, start))
dist[start] = 0
while q :
distance, node = heapq.heappop(q)
if distance > dist[node] :
continue
for n in graph[node] :
new_cost = n[1] + dist[node] # v2로 가는 노드의 거리 + 내가 방금 빼낸 관심노드까지의 최단거리
if new_cost < dist[n[0]] : # v2까지의 거리보다 짧으면
dist[n[0]] = new_cost
heapq.heappush(q, (new_cost, n[0]))
dijkstra(s)
for i in range(1, v+1) :
if dist[i] == INF :
print("INF")
else :
print(dist[i])min heap에서 최솟값을 빼내는 과정은 시간 복잡도 O(logN)에 가능하며, 큐에 들어갈 수 있는 최대 개수는 간선의 개수만큼이므로, 위 코드의 시간 복잡도는 O(E * logV) 이다. (V : 노드 수, E : 간선 수)
