다익스트라 알고리즘이 한 정점에서 다른 모든 정점까지의 최단거리 였다면, 플로이드 와샬 알고리즘은 임의의 정점에서 임의의 정점까지의 최단거리 를 다루는 알고리즘이다.

예를 들어, 어떤 그래프가 주어졌을 때 1에서 4로의 최단거리, 3에서 6으로의 최단거리는 동시에 구할 수 없다. 다익스트라 알고리즘은 출발점을 정하고 그 출발점을 기준으로 하기 때문이다.

반면 플로이드 와샬 알고리즘은 한 사이클의 연산을 통해 전체 그래프 상의 임의의 두 점 사이의 최단 거리를 구할 수 있다.

진행 방식

"두 점 사이에 어떤 점을 경유할 것인가?"

이것이 바로 플로이드 와샬 알고리즘의 골자이다.

전체 v개의 정점들 중 어떤 임의의 서로 다른 두 정점 i, j가 있다. 이 두 정점 사이의 최단 경로가 존재한다고 하자, 즉 어디를 경유하든 일단 갈 수는 있다고 가정하자.

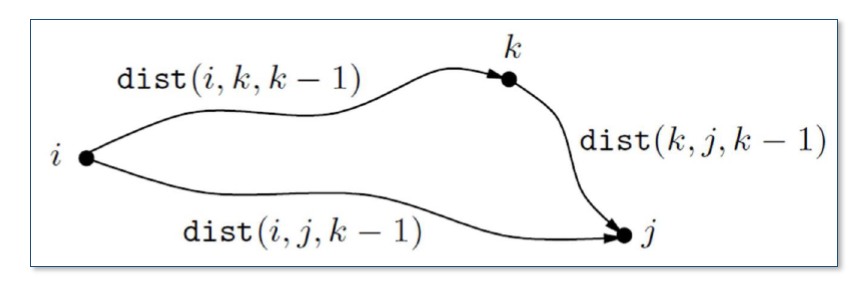
바로 i에서 j로 가는 간선이 있고 마침 그것이 최단 경로라면 매우 좋겠지만, 다른 점을 경유해서 가는 것이 최단 경로일 수도 있다.

이 때, 1~v 사이에는 그 최단 경로를 만드는 경유 정점이 반드시 있다. 이건 당연하다.
그럼, 모든 점에 대해서 일일이 경유를 찍어 보면 v번 중 한번은 반드시 걸린다.

그 점 하나만 경유하라는 법은 없다. 다만 그 점은 무조건 경유해라 이다.

즉 i부터 k까지의 거리 + k부터 j까지의 거리 에서 k를 1부터 v까지 돌리면 무조건 답을 찾을 수 있다.

파이썬 코드로 구현해 보자

구현

import sys
input = sys.stdin.readline

n = int(input())
v = int(input())
INF = 9999999
graph = [[INF] * (n+1) for _ in range(n+1)]

for _ in range(v) :
    v1, v2, c = map(int, input().split())
    graph[v1][v2] = c
    
for i in range(1, n+1) :
    graph[i][i] = 0

for k in range(1, n+1) :
    for i in range(1, n+1) :
        for j in range(1, n+1) :
            graph[i][j] = min(graph[i][j], graph[i][k] + graph[k][j])
            

for i in range(1, n+1) :
    for j in range(1, n+1) :
        if graph[i][j] == INF :
            print("0", end=" ")
        else :
            print(graph[i][j], end=" ")
    print()

3중 for문을 돌린다. 가장 바깥 for문 k는 '반드시 경유할 점' 이다.

그리고 i부터 j까지의 거리를 구하되, i~k, k~j의 합을 구해서 이 중 최솟값을 찾는다.

한계

무식하고 확실한 풀이이다. 3중 for문을 돌리기 때문에 O(N^3)이라는 무시무시한 시간 복잡도를 자랑하는지라, n이 1,000만 되더라도 계산 횟수가 10억 회가 된다.

n이 충분히 작아서 O(N^3)으로도 풀 수 있는 조건일 때 사용하면 좋을 것이다.