1. 선형회귀(linear regression)
- 1) 단순 회귀 : y = ax+b의 형태의 회귀선을 만드는 거다.
- 2) 다중 회귀 : 변수의 개수에 따라서, y = a1x1 + a2x2 + ...+ a_n x_n의 회귀선이 생성된다.
9) 변수선택
변수를 적절하게 선택해야 과대적합이 발생하지 않는다.
변수들의 가중치가 동일하게 책정됨으로, 의미 없는 변수에 쓸데없는 가중치를 갖게 해서는 안된다.
다른 변수들이 특정 변수와 연관이 있다고 생각이 된다면, 해당 변수를 target으로 놓고, r2값을 구해본다.
r2값이 높다면, 변수의 독립성이 낮다는 의미이고, 이는 다중공선성 문제를 일으킴으로, 해당 변수를 제거해준다.
- 3) 가중치 coef_ : 기울기(a)
- 4) 편향 intercept_ : 절편(b)
ex)
<복습 우리가 했던 것> #모델링 from sklearn.linear_model import LinearRegression model = LinearRegression() model.fit(x_train, y_train) y_pred = model.predict(x_test) sklearn.metrics from Mean_absolute_error, r2_score --------------------------------------------------------------------------- <새로운 거> #회귀 계수 확인 print(list(x)) #df를 list(df) 하면 컬럼만 깔끔하게 나옴 print(model.coef_.round(2)) print(model.intercept_) <출력> ['CompPrice', 'Income', 'Advertising', 'Population', 'Price', 'Age', 'ShelveLoc_Good', 'ShelveLoc_Medium', 'Education_11', 'Education_12', 'Education_13', 'Education_14', 'Education_15', 'Education_16', 'Education_17', 'Education_18', 'Urban_Yes', 'US_Yes'] [0.09, 0.01, 0.13, -0.0, -0.1, -0.05, 4.86, 2.03, -0.28, -0.22, -0.22, -0.13, 0.12, -0.37, -0.33, -0.38, 0.18, -0.24] 6.097879899078492
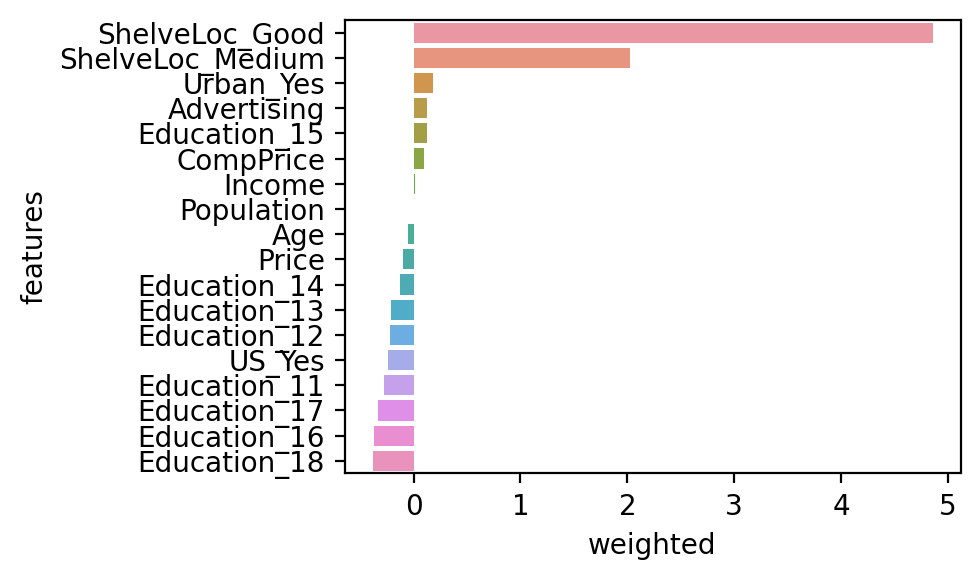
#시각화(다중 회귀일 때)
tmp = pd.DataFrame() # 비어있는 df 생성 tmp['features'] = list(x) tmp['weighted'] = model.coef_ tmp.sort_values(by='weighted', ascending = False, inplace = True) sns.barplot(y = 'features', x = 'weighted', data = tmp) <출력>
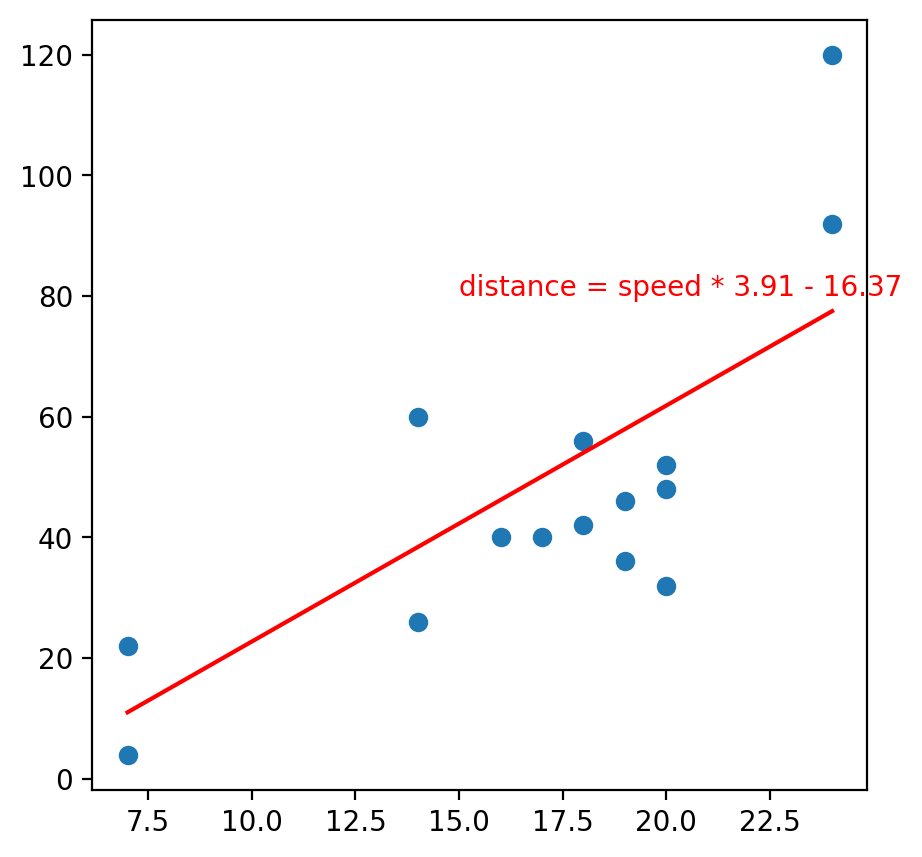
#시각화(단순 회귀일 때)
a = model.coef_ b = model.intercept_ speed = np.linspace(x_test.min(), x_test.max(), 5) # a 부터 b 까지 5개의 수를 뽑아낼 수 있음, range와 유사 distance = speed * a + b # y sns.scatterplot(x = x_test['speed'], y = y_test.values) plt.plot(speed, distance, color = 'r') plt.text(15, 80, 'distance = speed * 3.91 - 16.37', color = 'r') <출력>