SimCSE: Simple Contrastive Learning of Sentence Embeddings (EMNLP / 2021) paper review

Contribution

• 간단한 contrastive sentence embedding framework인 SimCSE를 제안하였다.

• unsupervised approach :
  standard dropout을 noise로 사용하여 생성한 positive instance를 이용하여 contrastive learning에 사용하였다.

• supervised approach :
  NLI dataset의 annotated pair를 contrastive learning에 사용하였다.

• contrastive learning objective가 pretrained embedding의 anisotropic space를 좀 더 uniform하게 regularize할 수 있음을 증명하였다.

---

Background: Contrastive Learning

• 의미적으로 가까운 sample들의 embedding은 vector space 내에 가까이 위치하도록 하고, 먼 sample들의 embedding은 멀리 위치하도록 하는 learning method이다.

---

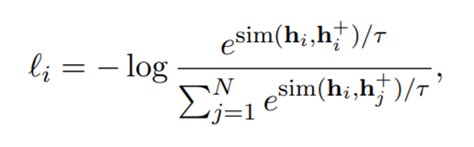
Background: Positive Instances

• visual representation의 경우, 같은 input에 대하여 다른 transformation을 적용하여 positive instance를 얻는다. (ex: cropping, flipping ...)

• NLP의 경우 descrete한 특성상 visual representation과 같은 transformation을 무작위로 적용할 수 없으므로 positive instance를 생성하는 데에 많은 제약이 따른다.

• 따라서 이 논문에서는 intermediate representation에 standard dropout을 적용하여서 positive instance를 생성하여 사용하였다.

---

Background: Alignment and Uniformity

• alignment는 positive pair의 distribution이 주어졌을 때, instance 쌍의 embedding 간의 expected distance를 계산한다.
  

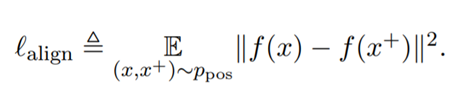
• uniformity는 embedding들이 vector space 내에 얼마나 uniform하게 분포되어 있는지를 측정한다.
  

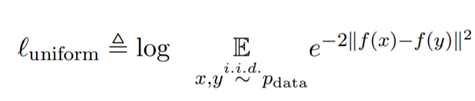
• 이 두 metric은 contrastive learing의 objective에 잘 align된다.
  => positive instance끼리는 가까이 위치해야하고, random intance들의 embedding은 hypersphere 내에 흩뿌려져 있어야함.

---

Architecture

---

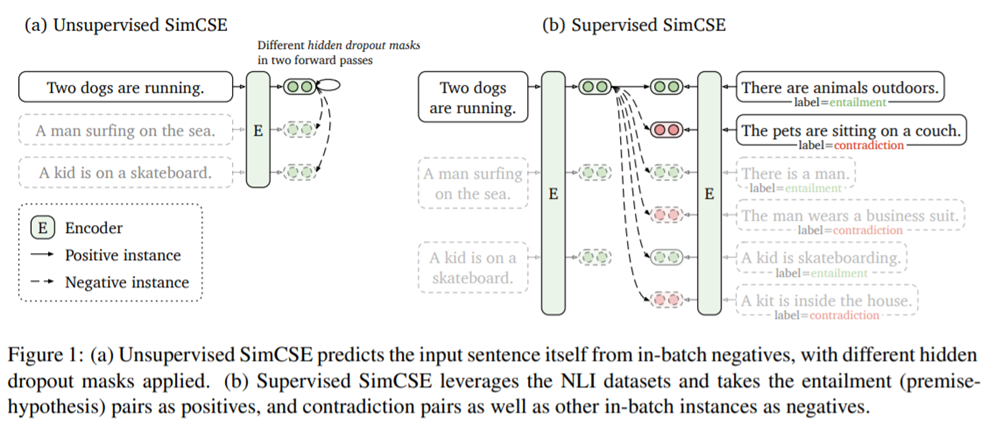
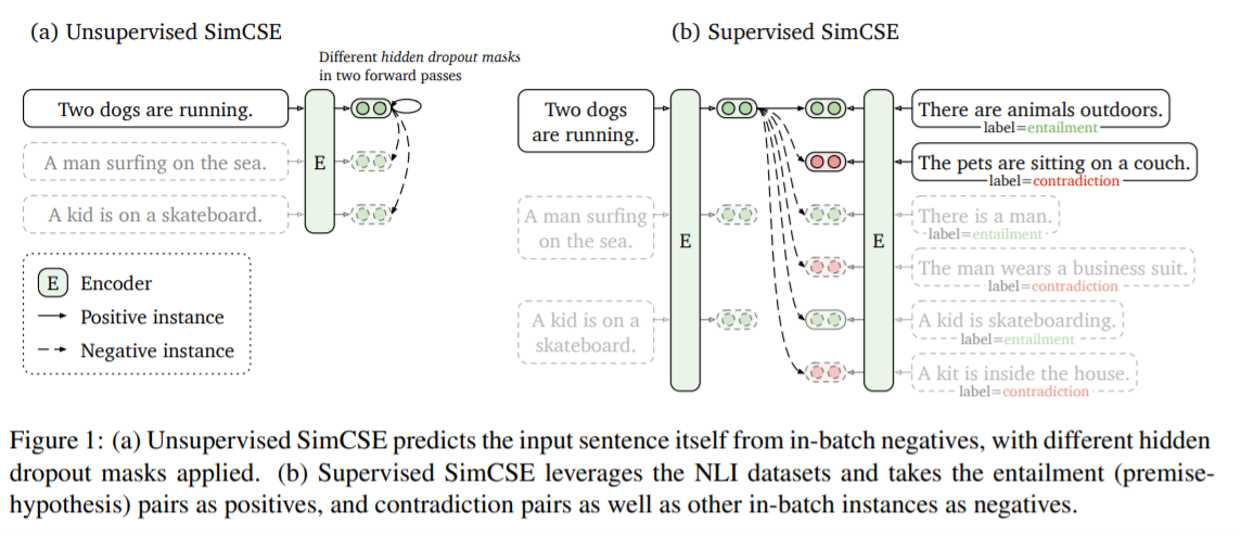
Unsupervised SimCSE

• encoder에 같은 input을 두 번 통과시켜 다른 dropout mask가 적용된 2개의 embedding을 얻는다. 이를 positive pair로 사용한다.
  (z term은 Transformer의 dropout mask를 의미한다.)

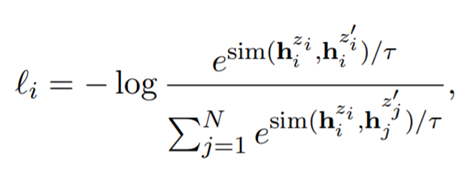
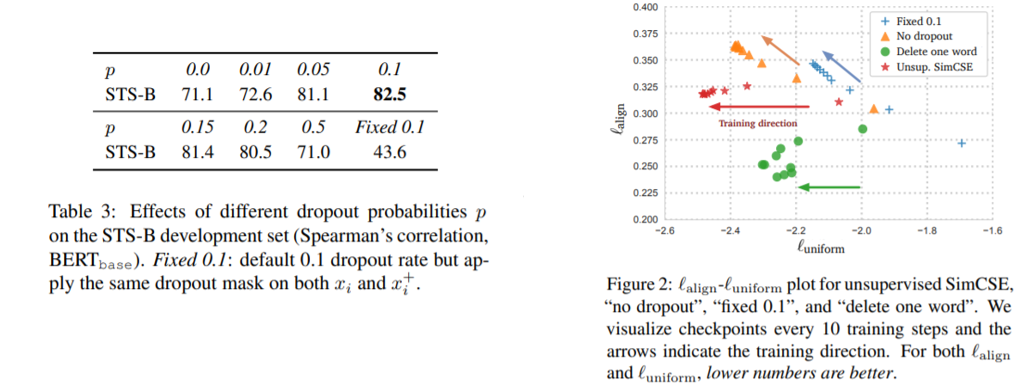
• 다른 augmentation 기법을 사용하였을 때보다 unsupervised SimCSE의 경우에서 더 높은 performance를 가진다. 또한 두 개의 encoder를 사용하여 positive instance를 생성하는 것보다 한 개의 encoder를 사용하였을 때의 경우가 더 좋은 performance를 가지는 것을 확인할 수 있다.

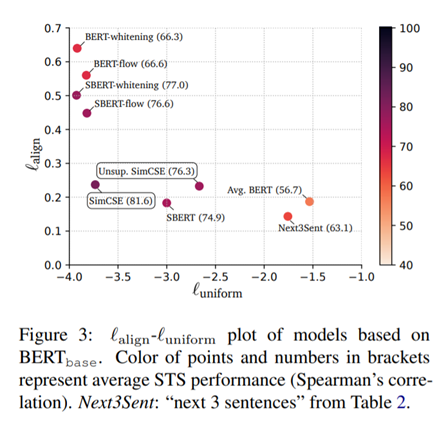
• Table 3은 dropout rate에 따른 performance table이다. 기존 transformer와 마찬가지로 0.1을 사용하였을 때 가장 좋은 성능을 낸다. 또한 Figure 2는 uniformity와 alignment 측면에서의 성능 비교 figure로 두 metric 모두 값이 낮을수록 좋은 model로 평가한다. 다른 option들을 사용하였을 때에 비하여 unsupervised SimCSE에서가 uniformity와 alignment 두 측면에서 다 좋은 성능을 보이는 것을 확인할 수 있다.

---

Supervised SimCSE

• supervised dataset을 SimCSE approach에서 alignment를 improve하는 데에 있어 더 나은 training signal로 줄 수 있는지에 대한 연구이다.

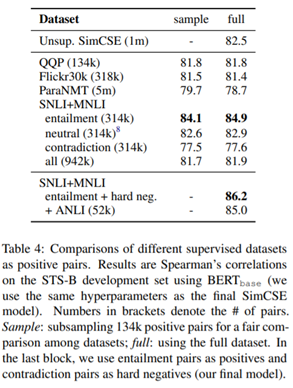
• 여러 dataset 중, NLI (SNLI + MNLI) dataset을 사용하였을 때가 가장 좋은 성능을 내었다고 한다. NLI dataset의 entailment를 positive pair로 사용한 것에 추가로, contradiction sample을 negative instance로 사용하였을 때 성능 개선을 이루었다고 한다.
  
  entailment: 하나의 전제가 주어졌을 때, 그에 따른 가정이 True일 때
  neutral: 하나의 전제가 주어졌을 때, 그에 따른 가정이 T/F를 알 수 없을 때
  contradiction: 하나의 전제가 주어졌을 때, 그에 따른 가정이 False일 때
  

• negative instance를 추가하여 확장한 loss function은 다음과 같다.
  

  ---

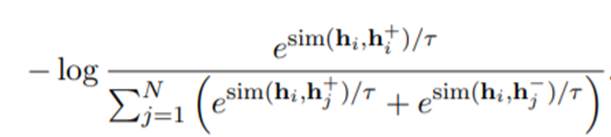
  Connection to Anisotropy

• language representation에서의 Anisotropy 문제는 vector space의 narrow cone 안에 embedding들이 분포하고 있어 embedding의 expressiveness가 제한되는 현상을 의미한다.

• anisotropy 문제는 uniformity와 관련이 있다. 둘 다 vector space내에 embedding이 고르게 분포하는 것을 지향한다. 따라서 contrastive learning objective는 uniformity를 improve할 수 있고 그에 따라 anisotropy 문제도 자연적으로 해결될 수 있다고 한다.

• 수식적 증명
  
  
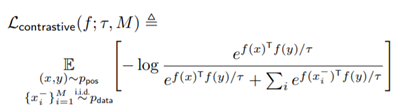
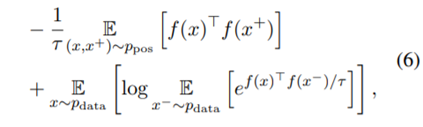
  위의 contrastive loss를 (6)번 식으로 변형할 수 있다.
  
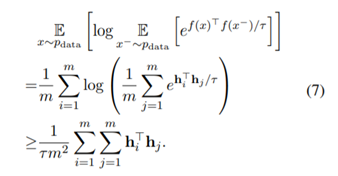
  그렇게 변형된 식은 Jensen's inequality( f(E(x)) <= E(f(x)) )에 의해 (7)번 식으로 유도될 수 있다.
  

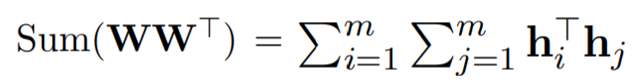
  또한 hidden representation의 multiplication의 합은 다음과 같이 weight matrix의 계산으로 변형될 수 있다. 이 논문에서 h를 normalize 하였기 때문에 WW'의 diagonal값은 1이다. 그리고 sum(WW')은 WW'의 가장 큰 eigenvalue의 upper bound가 된다. 그래서 (6)번 식을 minimize할 때 WW'의 top eigenvalue를 minimize하게되고 그에 따라 embedding space의 singular spectrum이 flatten된다. 따라서 contrastive learning이 anisotropy 문제를 해결할 수 있음이 수식적으로 증명된다.

---

Experiment

---

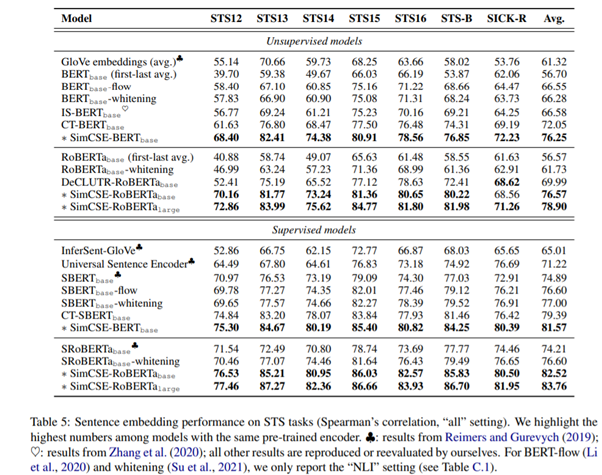
Conclusion

• 이 논문에서는 simple contrastive learning framework를 제안하고 있다.

• unsupervised approach에서는 dropout을 noise로 사용하여 생성한 positive pair를, 그리고 supervised approach에서는 NLI dataset을 이용한 supervised approach를 사용하여 contrastive learning을 진행하였다.