트리

그래프 중 하나로 그래프의 특징처럼 정점과 간선으로 이루어져 있고, 트리 구조로 배열된 일종의 계층적 데이터의 집합이다.

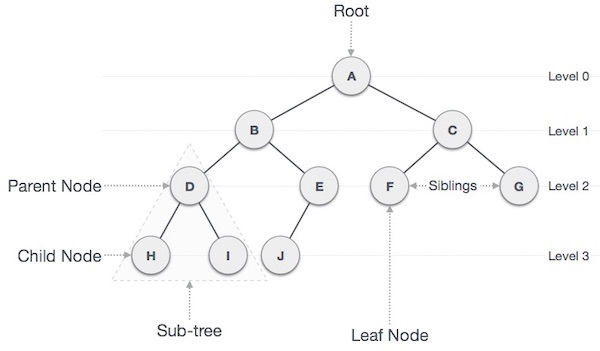
• 루트 노드, 내부 노드, 리프 노드 등으로 구성된다.

📌 구성

data class TreeNode<T>(
	var data: T,
    var left: TreeNode<T>?,
	var right: TreeNode<T>?
)

class Tree{
    var root : TreeNode<String>? = null

    // 트리 추가
    fun add(data: String, left: String, right: String){
        // 루트가 NULL 일 때 (트리 내에 존재하지 않을 때)
        if(root == null){
            // 새로 생성
            if(data != ".") root = TreeNode(data)
            if(left != ".") root!!.left = TreeNode(left)
            if(right != ".") root!!.right = TreeNode(right)
        }
        // 트리 내에 존재할 때
        else search(root!!,data,left,right)
    }

    private fun search(root: TreeNode<String>, data: String, left: String, right: String){
        // 찾았을 때, left right 연결
        if(root.data == data){
            if(left != ".") root!!.left = TreeNode(left)
            if(right != ".") root!!.right = TreeNode(right)
        }

        // 못 찾았을 때, 좌우 탐색
        else {
            if(root.left != null) search(root.left!!,data,left,right)
            if(root.right != null) search(root.right!!,data,left,right)
        }
    }
}

📌 탐색

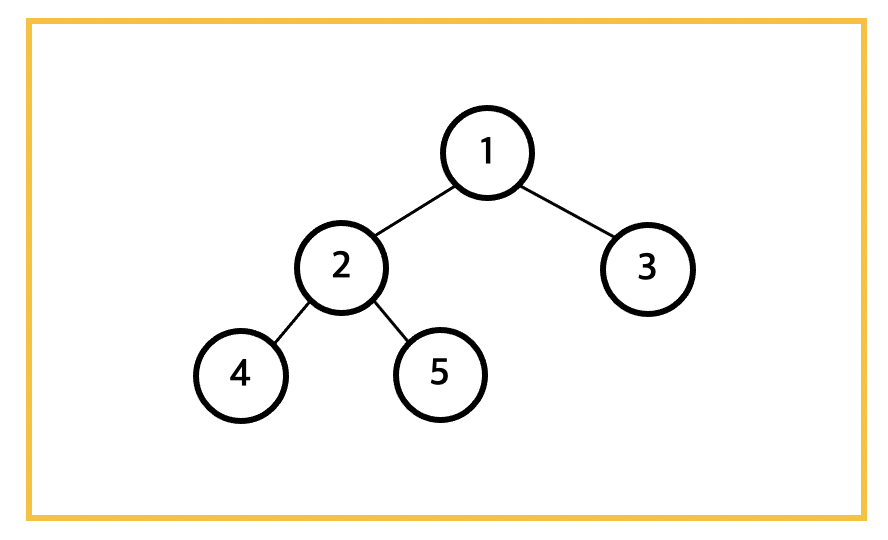
전위 탐색(Pre-order traversal)

루트 노드를 먼저 방문하고, 왼쪽 서브 트리를 방문하고, 오른쪽 서브 트리를 방문하는 탐색 방법이다.

• 모든 탐색은 각 서브 트리로 방문(진입)했을 때도 같은 규칙을 적용한다.
• 위 트리에 대해서 전위 탐색을 진행했을 때 1 - 2 - 4 - 5 - 3 순서대로 탐색을 진행한다.

// 루트 -> 왼쪽 -> 오른쪽
fun preOrder(root: TreeNode<String>){
	print(root.data)
    if(root.left != null) preOrder(root.left!!)
    if(root.right != null) preOrder(root.right!!) 
}

중위 탐색(In-order traversal)

왼쪽 서브 트리를 먼저 방문하고, 루트 노드(자신)을 방문하고, 오른쪽 서브 트리를 방문하는 탐색 방법이다.

• 위 트리에 대해서 중위 탐색을 진행했을 때 4 - 2 - 5 - 1 - 3 순서대로 탐색을 진행한다.

// 왼쪽 -> 루트 -> 오른쪽
fun preOrder(root: TreeNode<String>){
    if(root.left != null) preOrder(root.left!!)
    print(root.data)
    if(root.right != null) preOrder(root.right!!) 
}

후위 탐색(Post-order traversal)

왼쪽 서브 트리를 먼저 방문하고, 오른쪽 서브 트리를 방문하고, 마지막으로 루트 노드(자신)을 방문하는 탐색 방법이다.

• 위 트리에 대해서 후위 탐색을 진행했을 때 4 - 5 - 2 - 3 - 1 순서대로 탐색을 진행한다.

// 왼쪽 -> 오른쪽 -> 루트
fun preOrder(root: TreeNode<String>){
    if(root.left != null) preOrder(root.left!!)
    if(root.right != null) preOrder(root.right!!) 
    print(root.data)
}

📌 트리 종류

이진 트리(Binary Tree) : 각 노드의 자식이 최대 2개의 노드만을 가지는 Tree.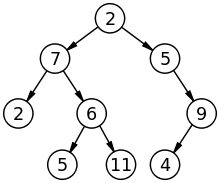

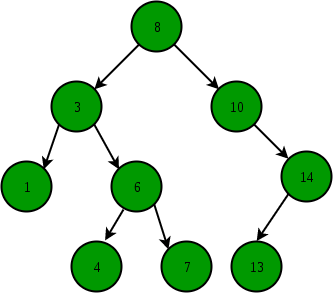
이진 탐색 트리(Binary Search Tree, BST) : 노드의 왼쪽 자식은 부모보다 작은 값을 가지고, 노드의 오른쪽 자식은 부모보다 큰 값을 가지는 이진 트리.

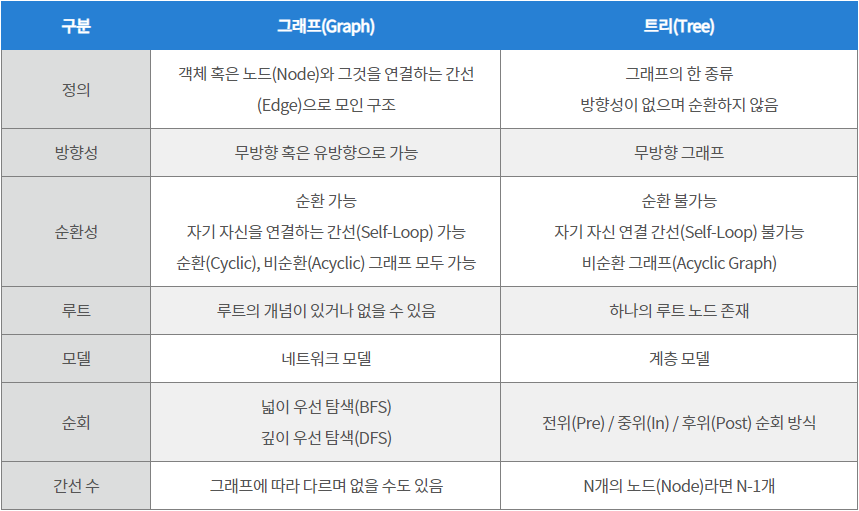
📌 그래프 vs 트리