정점과 간선으로 이루어진 자료 구조입니다.
📌 구성 요소
- 정점(Node) : 객체, 위치의 개념
- 간선(Edge) : 정점간의 연결선
📌 종류
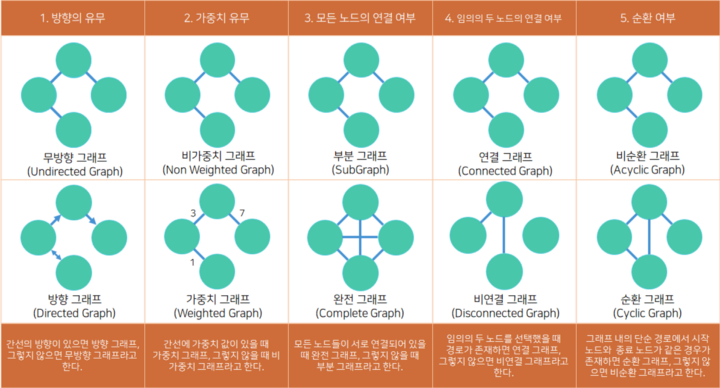
📌 구현
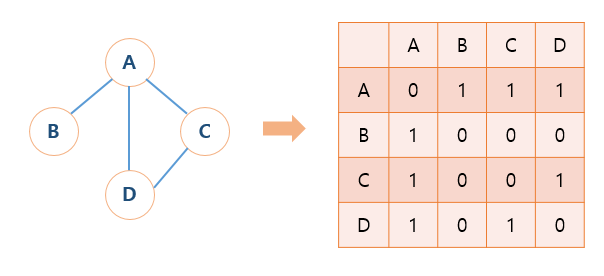
- 인접 행렬
2차원 배열을 이용하여 구현한 방법이다.
val graph = arrayOf(
arrayOf(0, 1, 1, 1),
arrayOf(1, 0, 0, 0),
arrayOf(1, 0, 0, 1),
arrayOf(1, 0, 1, 0)
)
for ((index1, adjacent) in graph.withIndex()) {
//기준 노드
val criteriaNode = when (index1) {
0 -> 'A'
1 -> 'B'
2 -> 'C'
3 -> 'D'
else -> 'X'
}
//기준 노드 출력
print("$criteriaNode : ")
for ((index2, connected) in adjacent.withIndex()) {
//기준 노드와 연결된 노드만 출력
if (connected == 1) {
val connectedNode = when (index2) {
0 -> 'A'
1 -> 'B'
2 -> 'C'
3 -> 'D'
else -> 'X'
}
print("$connectedNode ")
}
}
println()
}
/* 결과
A : B C D
B : A
C : A D
D : A C
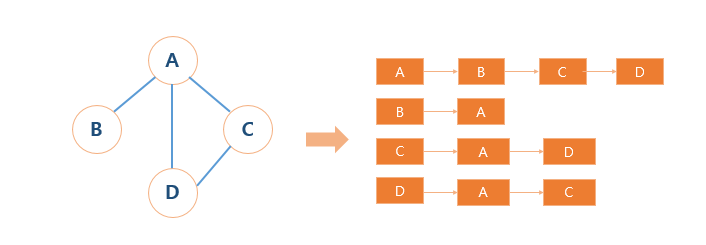
*/- 인접 리스트
연결 리스트를 이용하여 구현한 방법이다.
val graph = LinkedHashMap<Char, LinkedList<Char>>()
graph.run{
set('A', LinkedList())
get('A')?.run{
add('B')
add('C')
add('D')
}
set('B', LinkedList())
get('B')?.run{
add('A')
}
set('C', LinkedList())
get('C')?.run{
add('A')
add('D')
}
set('D', LinkedList())
get('D')?.run{
add('A')
add('C')
}
}
graph.forEach { a ->
print("${a.key}의 인접 리스트")
a.value.forEach { b ->
print(" -> $b")
}
println()
}
/* 결과
A의 인접 리스트 -> B -> C -> D
B의 인접 리스트 -> A
C의 인접 리스트 -> A -> D
D의 인접 리스트 -> A -> C
*/📌 인접 행렬 vs 인접 리스트
-
인접 행렬
장점
- 두 노드 간의 연결 관계를 확인하고 싶을 때 단지 인덱스로 접근하여 0인지, 1인지 확인하면 된다. 👉 O(1)
- 인접 리스트에 비해 구현이 쉽다.단점
- 모든 관계(연결되지 않은 것까지)를 저장하므로, 노드 개수가 많을수록 메모리가 불필요하게 낭비된다. 👉 O(노드의 수) -
인접 리스트
장점
- 연결된 정보만 (연결되지 않은 것은 제외) 저장하기에 메모리 낭비가 적다.
👉 O(간선의 수)단점
- 두 노드 간의 연결 관계를 확인하고 싶을 때는 탐색이 필요하기에 속도가 느리다. 👉 O(노드의 수)
📌 탐색 방법
- BFS(넓이 우선 탐색, Breadth-First-Search)
- DFS(깊이 우선 탐색, Depth-First-Search)
관련 포스팅은 여기
사용
- 네트워크
- 경로 찾기
- 순서 확인
- 연결성 확인