[Linear Algebra] Inner Product, Length, Orthogonality

Inner product

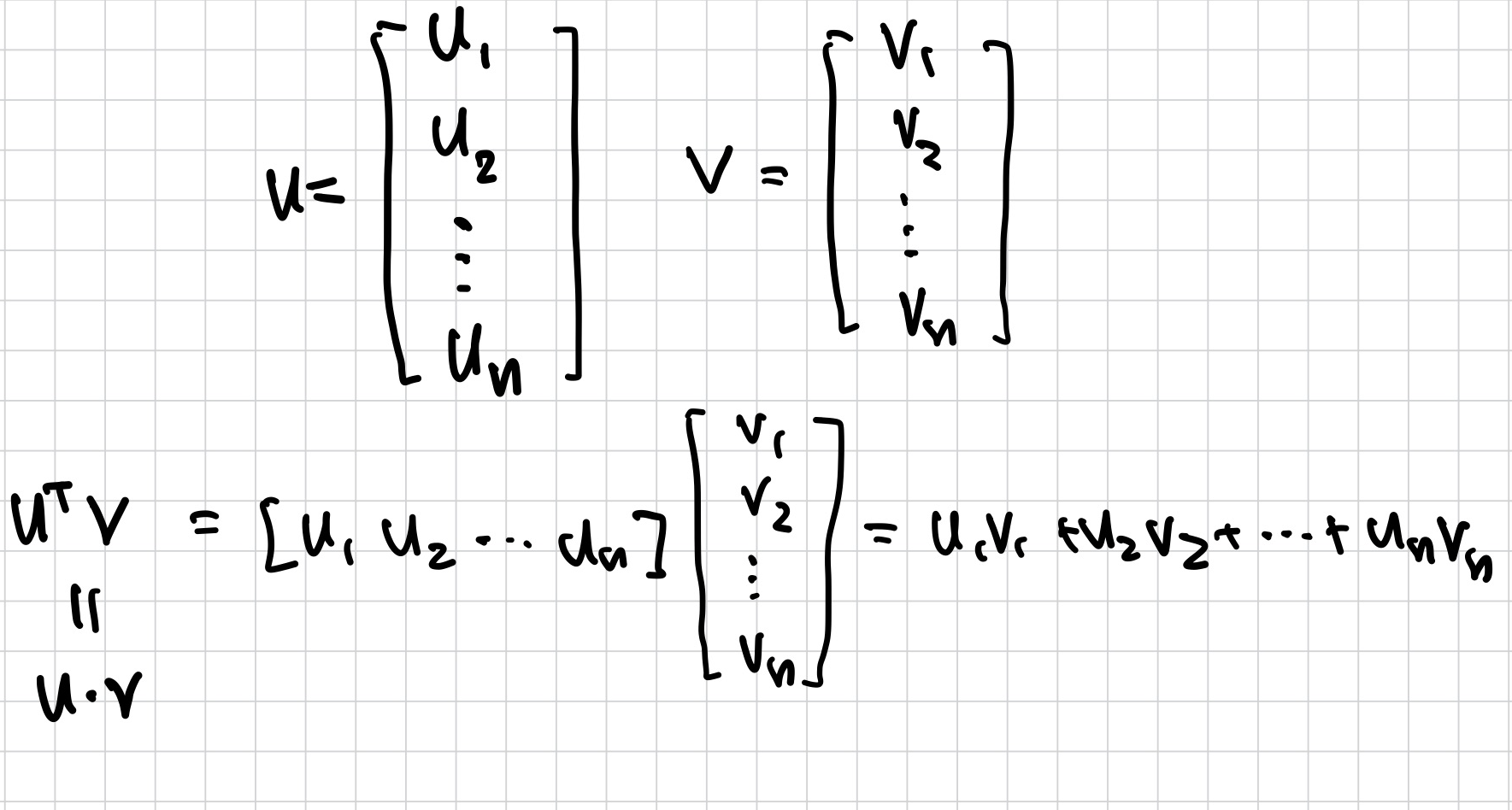
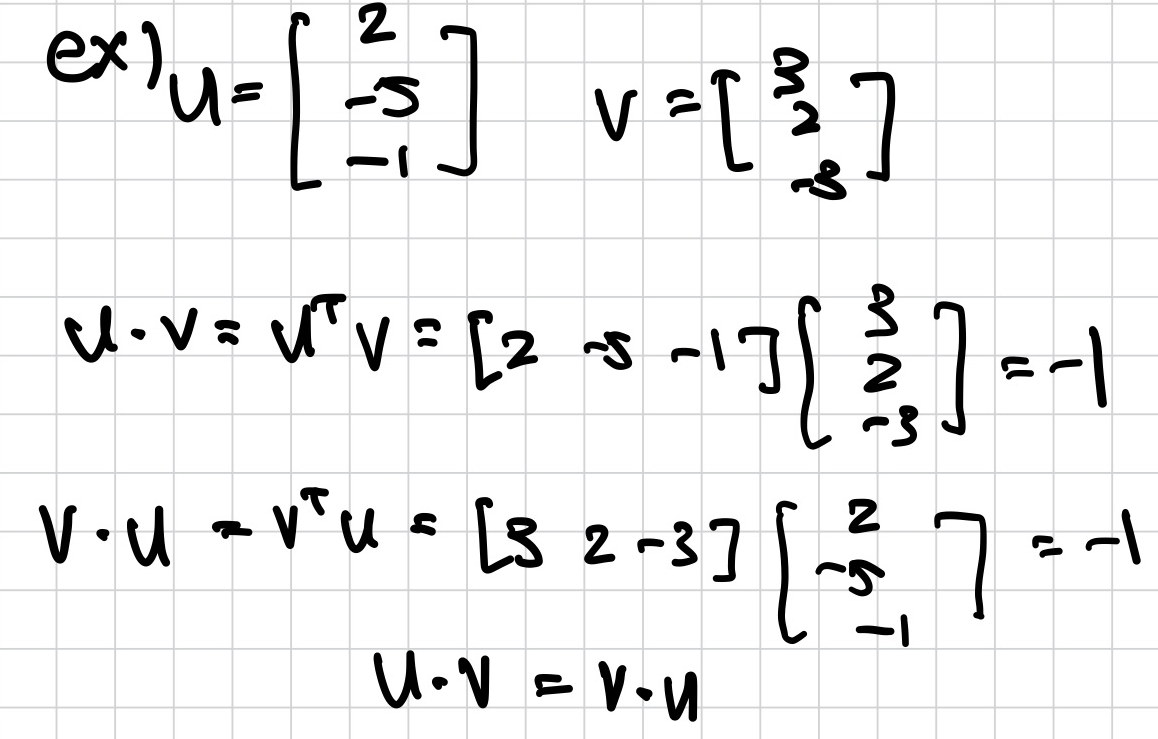
Theorem.

Length of a vector

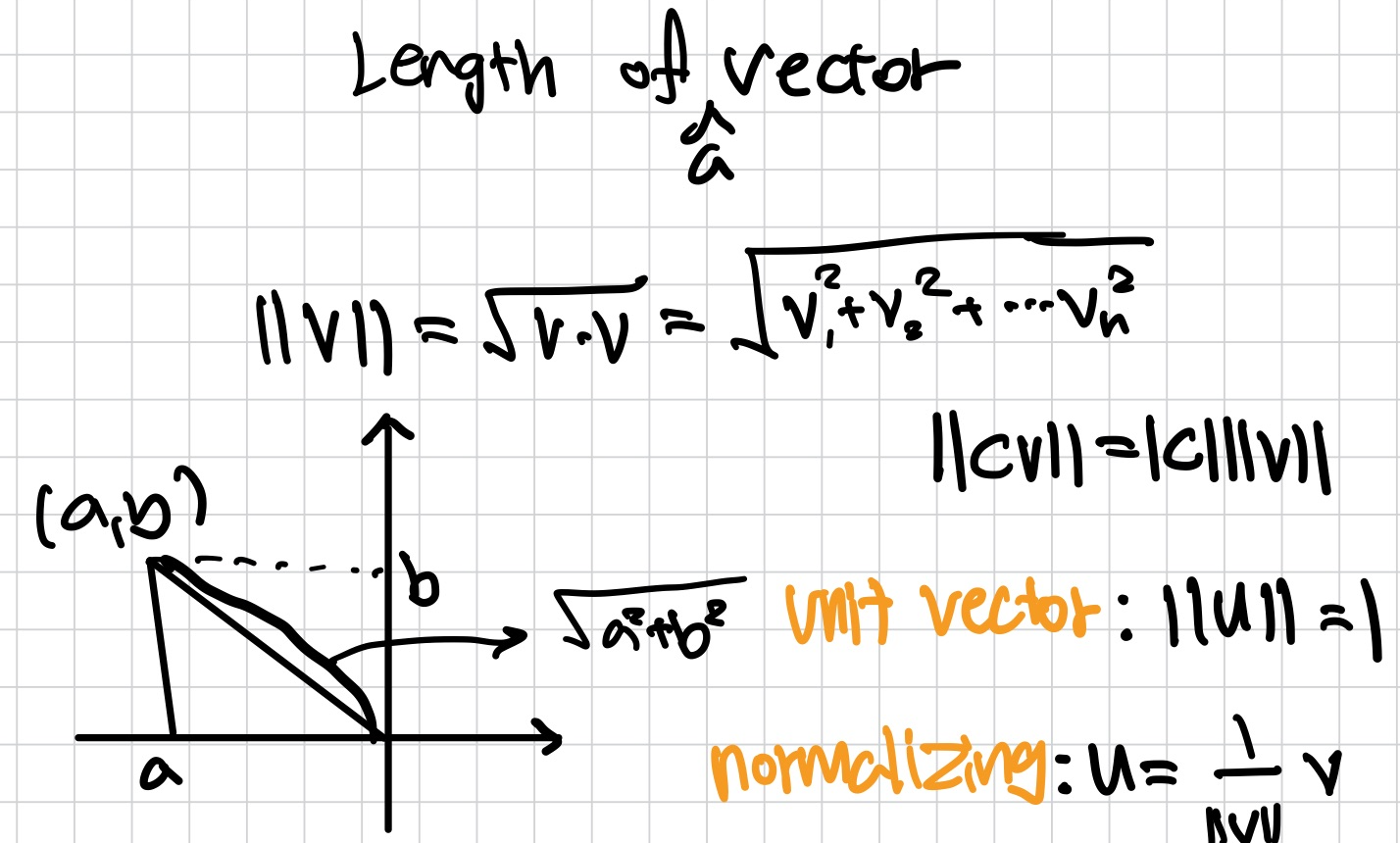
Distance in Rn

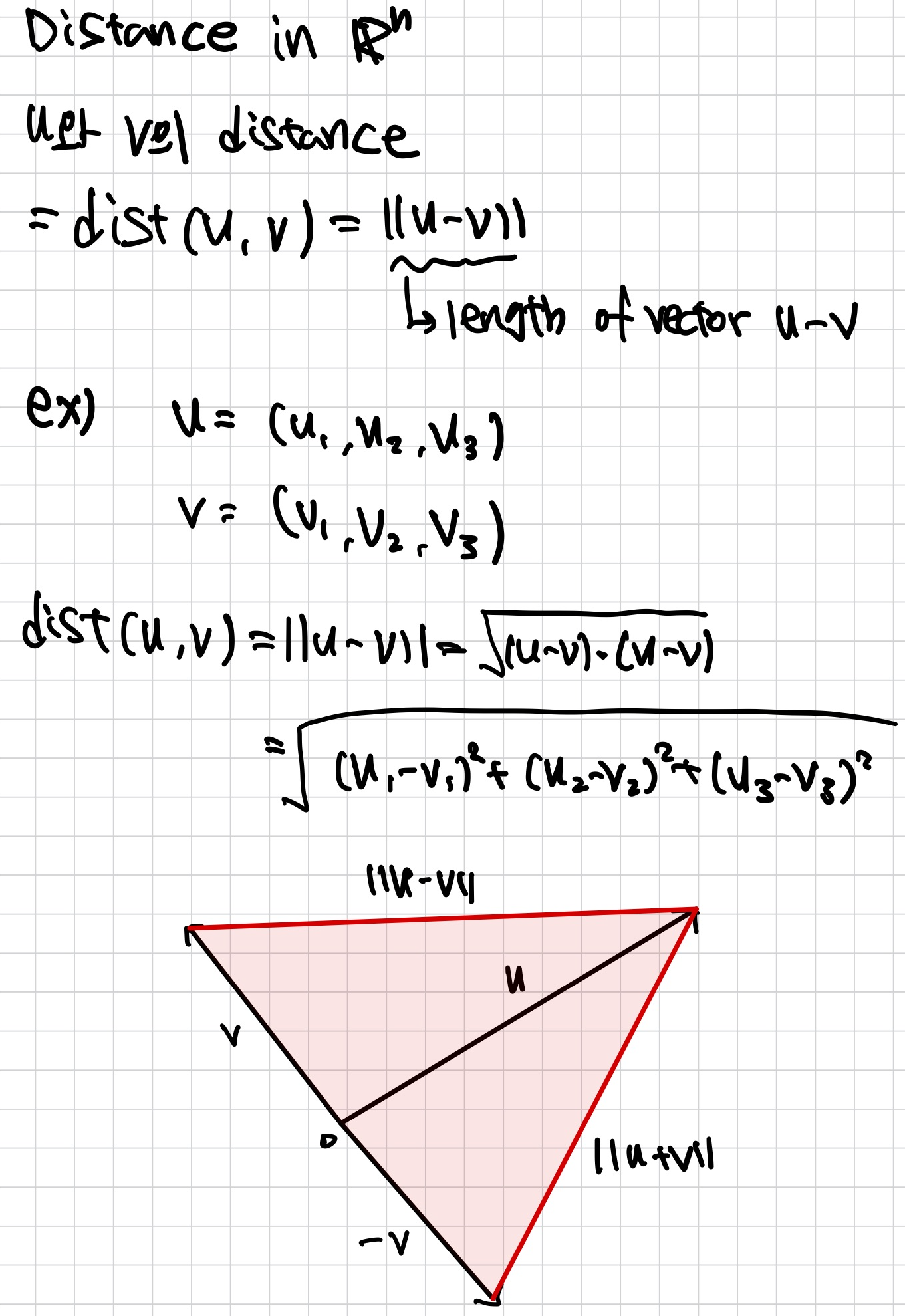
Orthogonal vectors

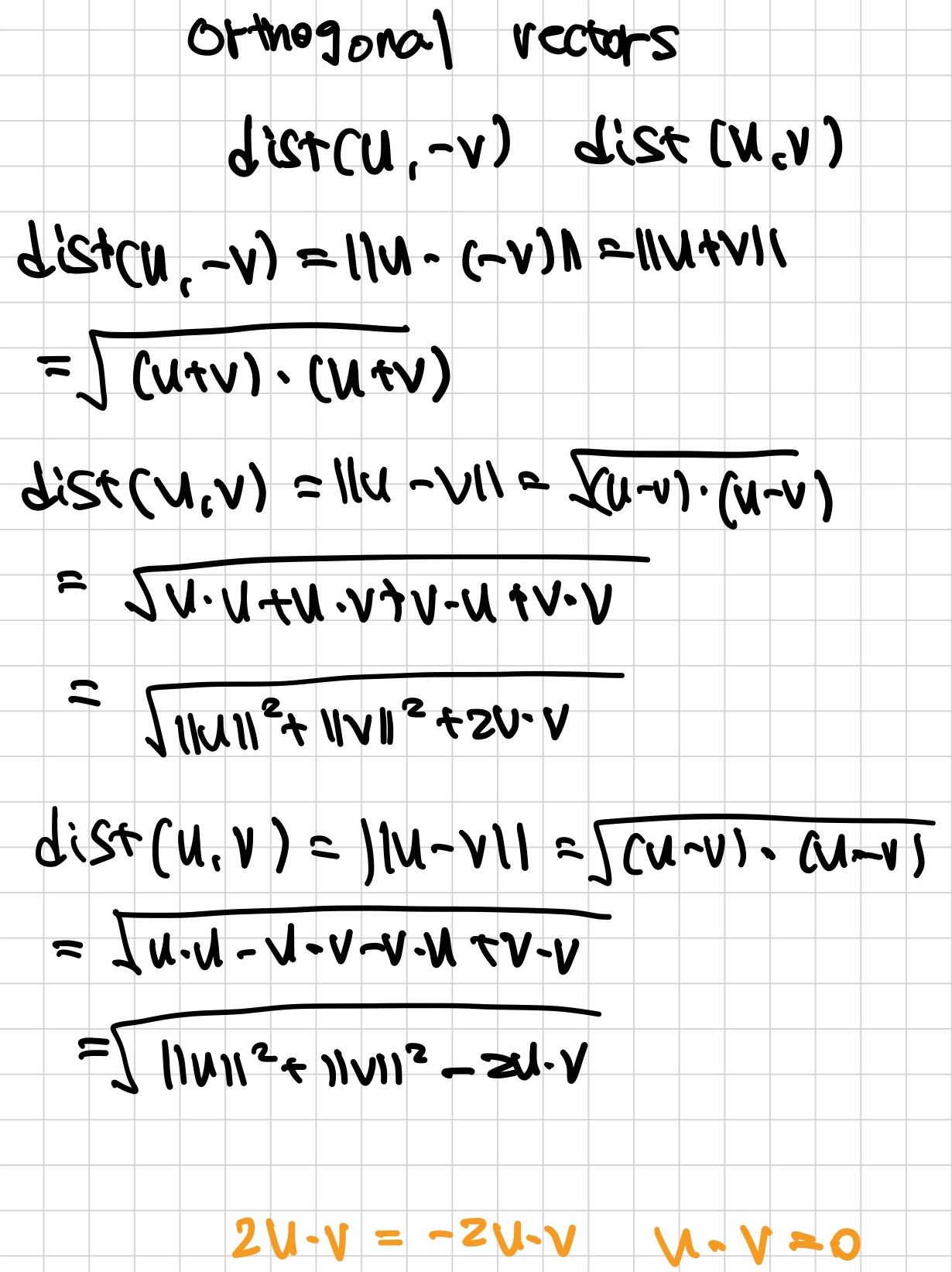
• 두 벡터 u·v=0이면, orthogonal이다.
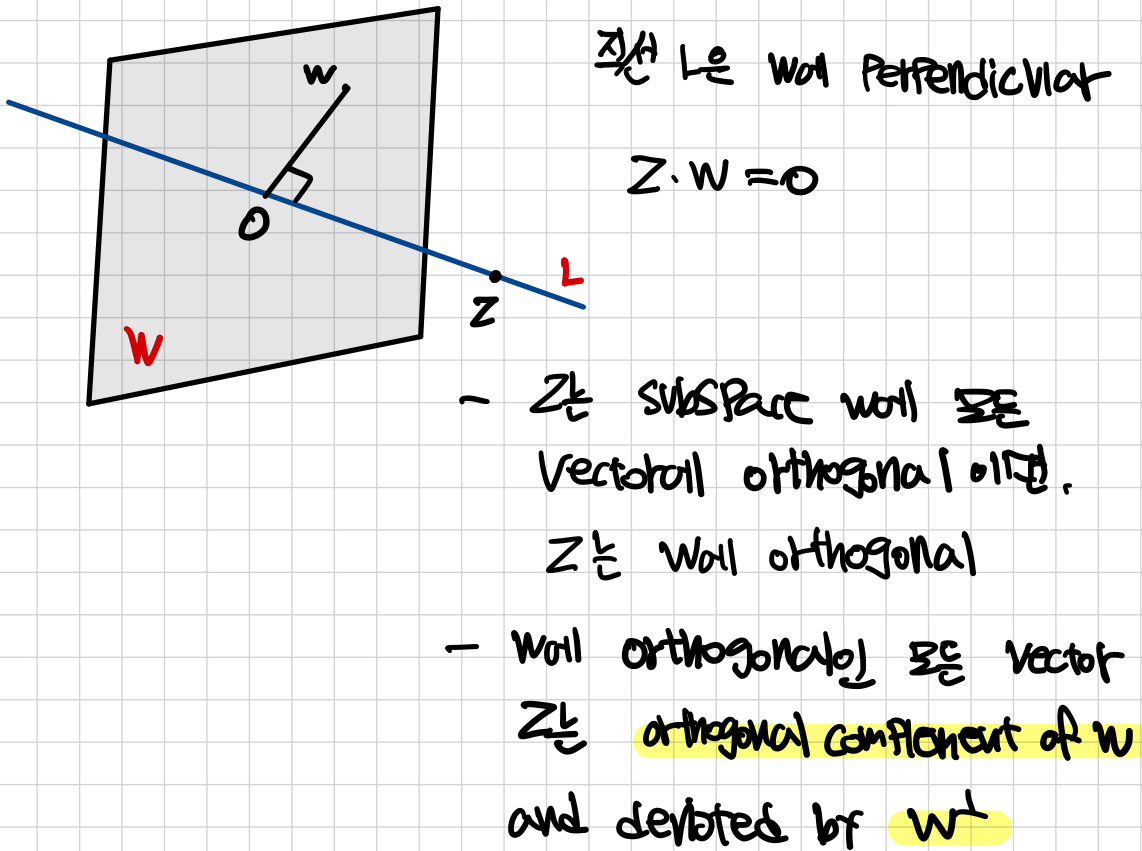
• zero vector는 Rn에 모든 벡터에 orthogonal이다.
  0Tv = 0

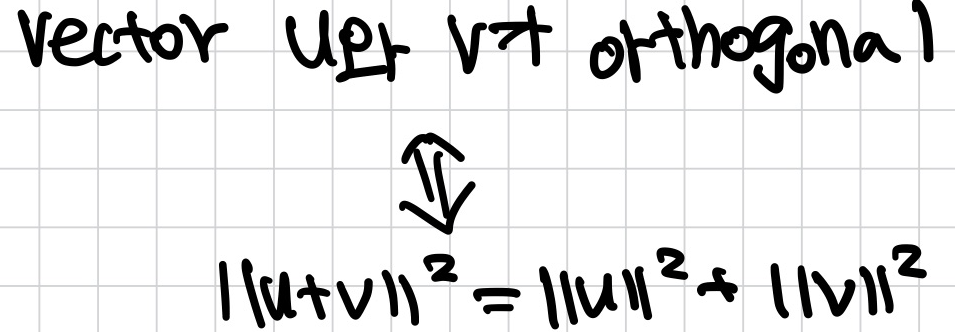
Theorem. Pythagorean Theorem

Orthogonal complements

Example

1. 벡터 y가 u,v와 orthogonal이다. y가 u+v에 orthogonal임을 보여라.

2. 벡터 y가 u,v와 orthogonal이다. y가 모든 w in Span {u,v}에 orthogonal이다.

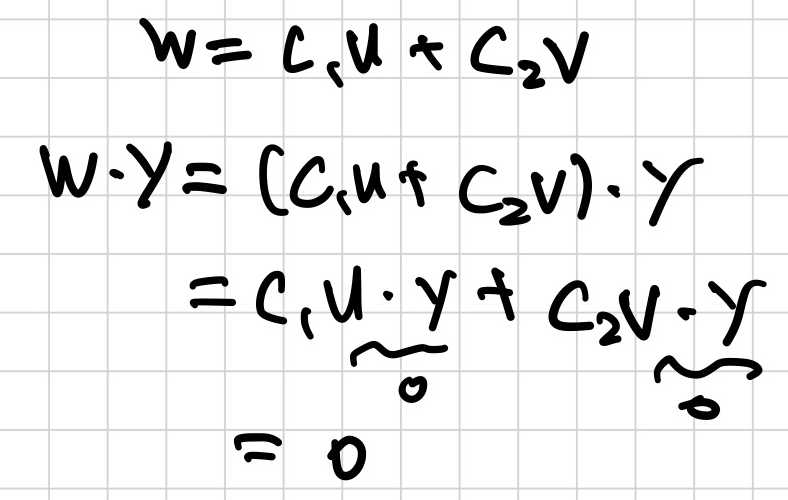
3. W = Span {v1, ... ,vp}이다. x가 각 vj에 orthogonal이면, x는 W에 모든 벡터에 orthogonal이다.

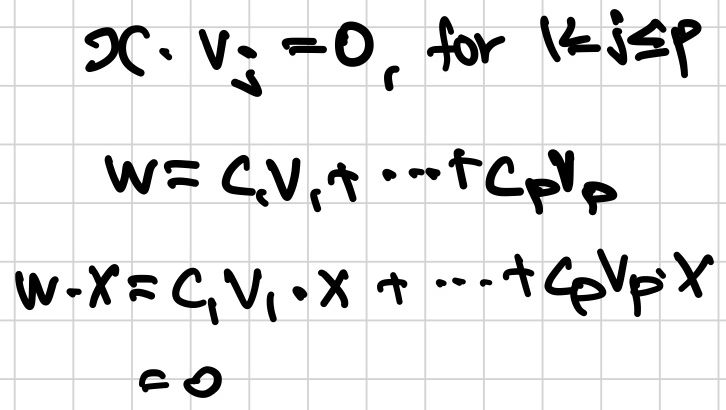
4. W가 Rn의 subspace이고, W⟂가 W에 모든 orthogonal vectors set이다. W⟂가 Rn의 subspace임을 보여라.

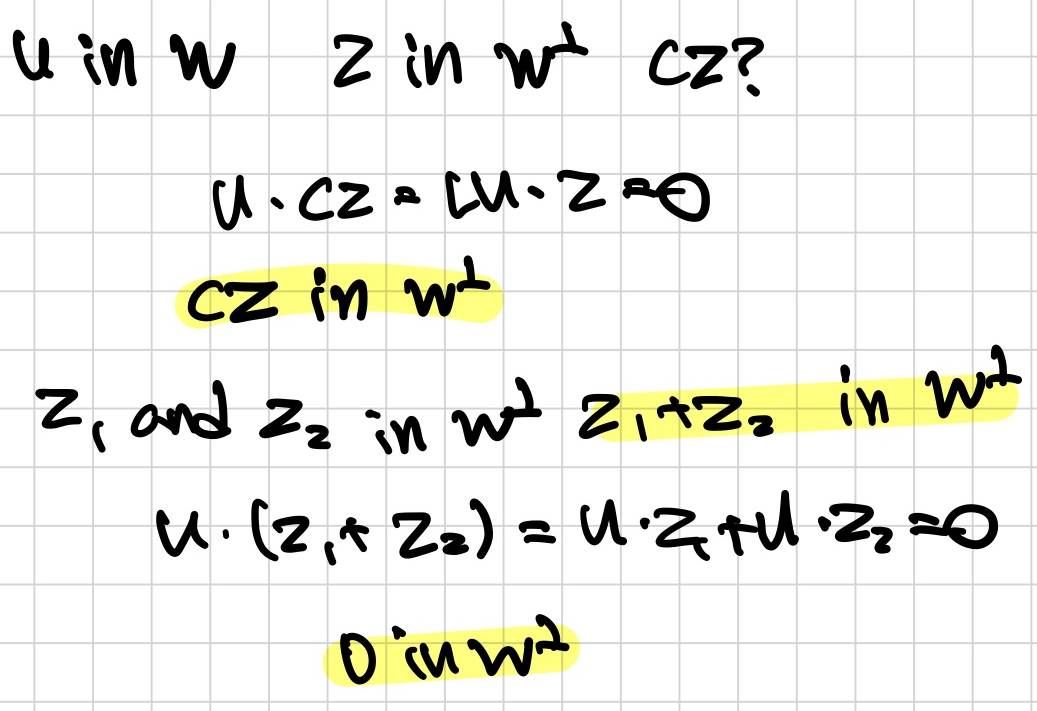
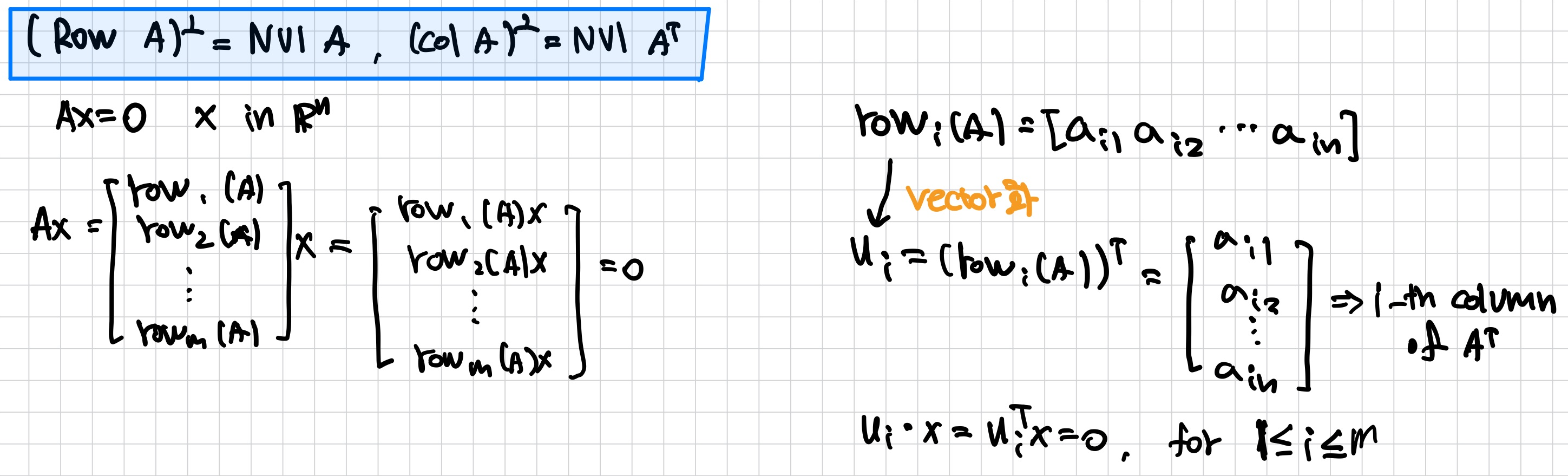
Theorem.

m x m matrix A
A의 row space의 orthogonal complement는 A의 null space이고, A의 column space의 orthogonal complement는 AT의 null space이다.