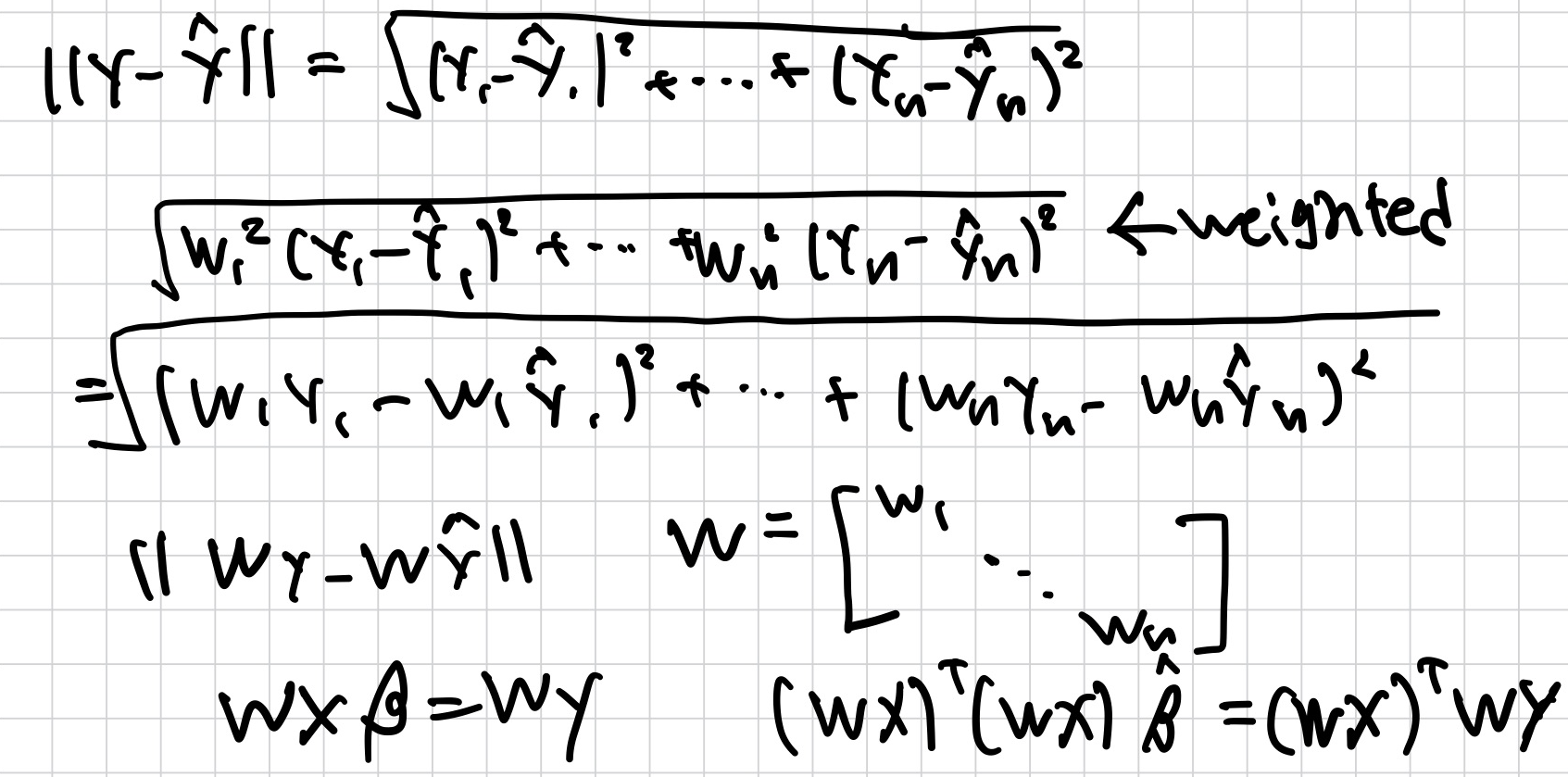[Linear Algebra] Gram-Schmidt Process & Least-Square Problems

Gram-Schmidt Process의 기본원리

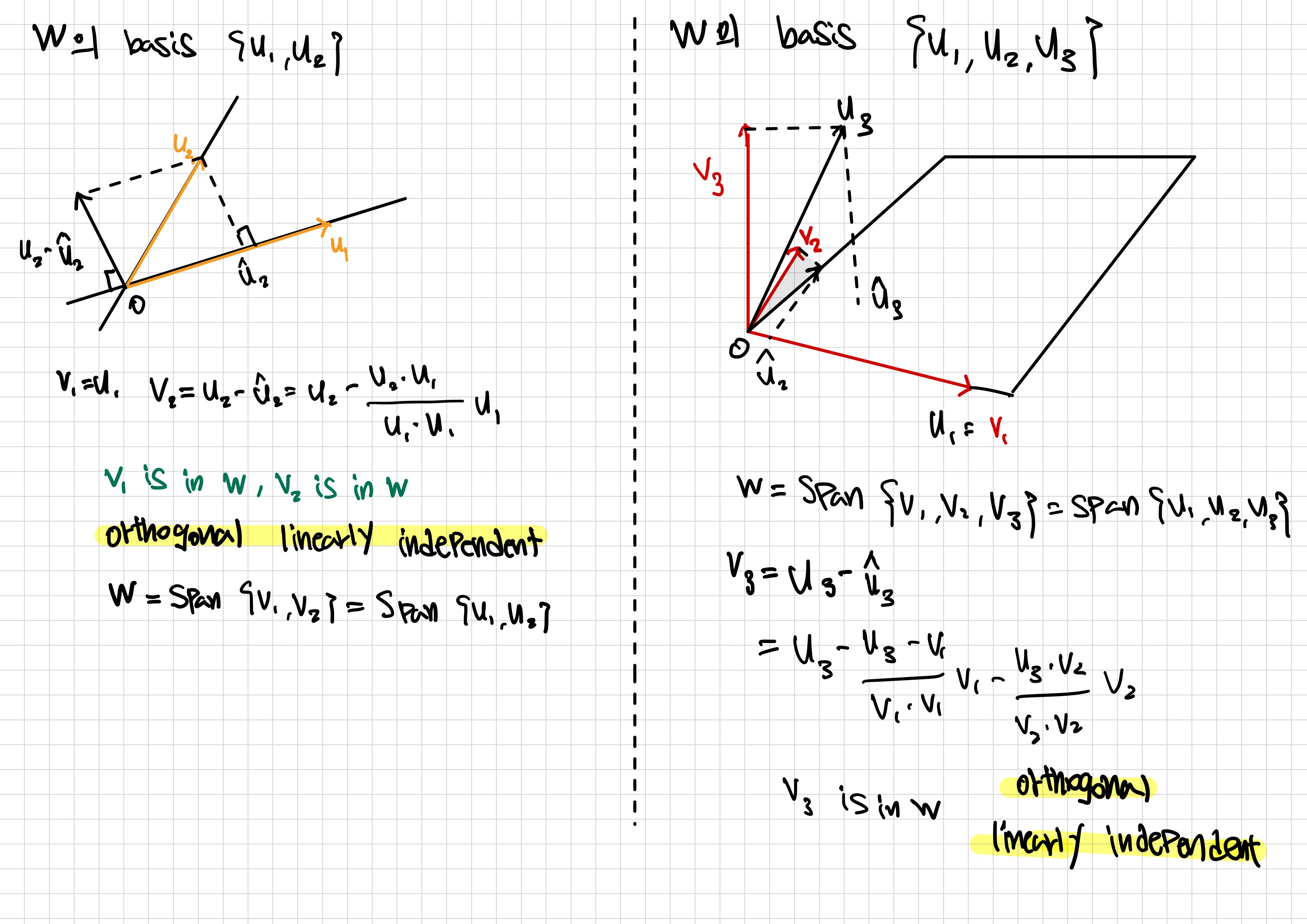
Gram-Schmidt Process

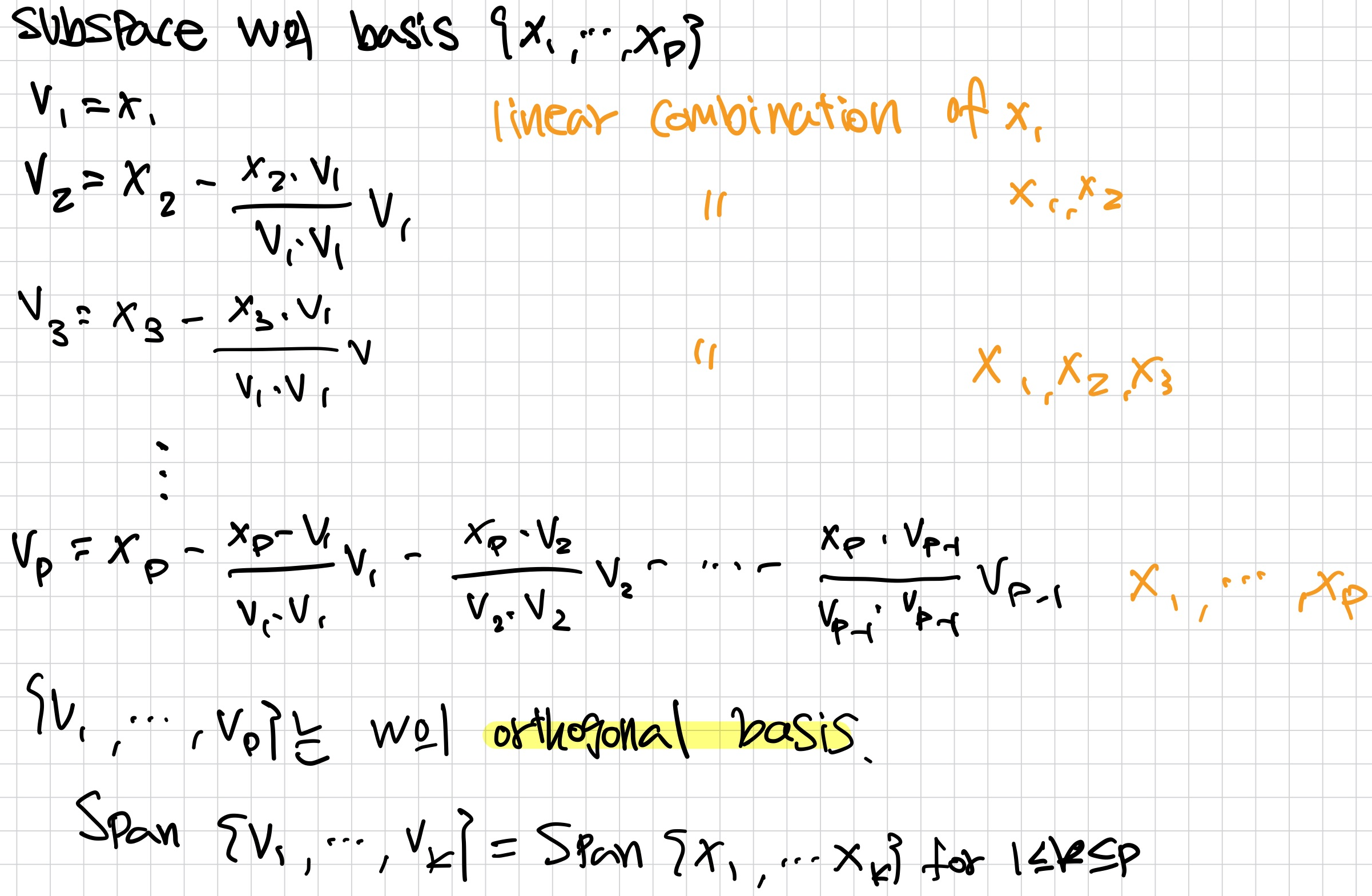
Orthonormal Basis

subspace W의 orthogonal basis를 normalizing한 set을 의미

QR factorization

• matrix m x n A가 linearly independent columns이면, A=QR로 factorization이 가능
  - Q는 Col A의 orthonormal basis m x n matrix 형태
  - R은 n x n upper triangular invertible matrix

QR factorization process

1. Gram-Schmidt 알고리즘을 통해 Col A의 orthonormal basis를 찾는다.
2. 1에서 구한 basis를 통해 matrix Q 구성
3. QTA = QT(QR) = IR = R
4. rkk<0 일 때, uk(-uk)와 rkk부터 rkn의 부호를 바꾼다.

Least-Squares Solution

m x n matirx A와 b가 Rm가 있다. Ax = b의 least-squares solution이 Rn에 x̂이다.

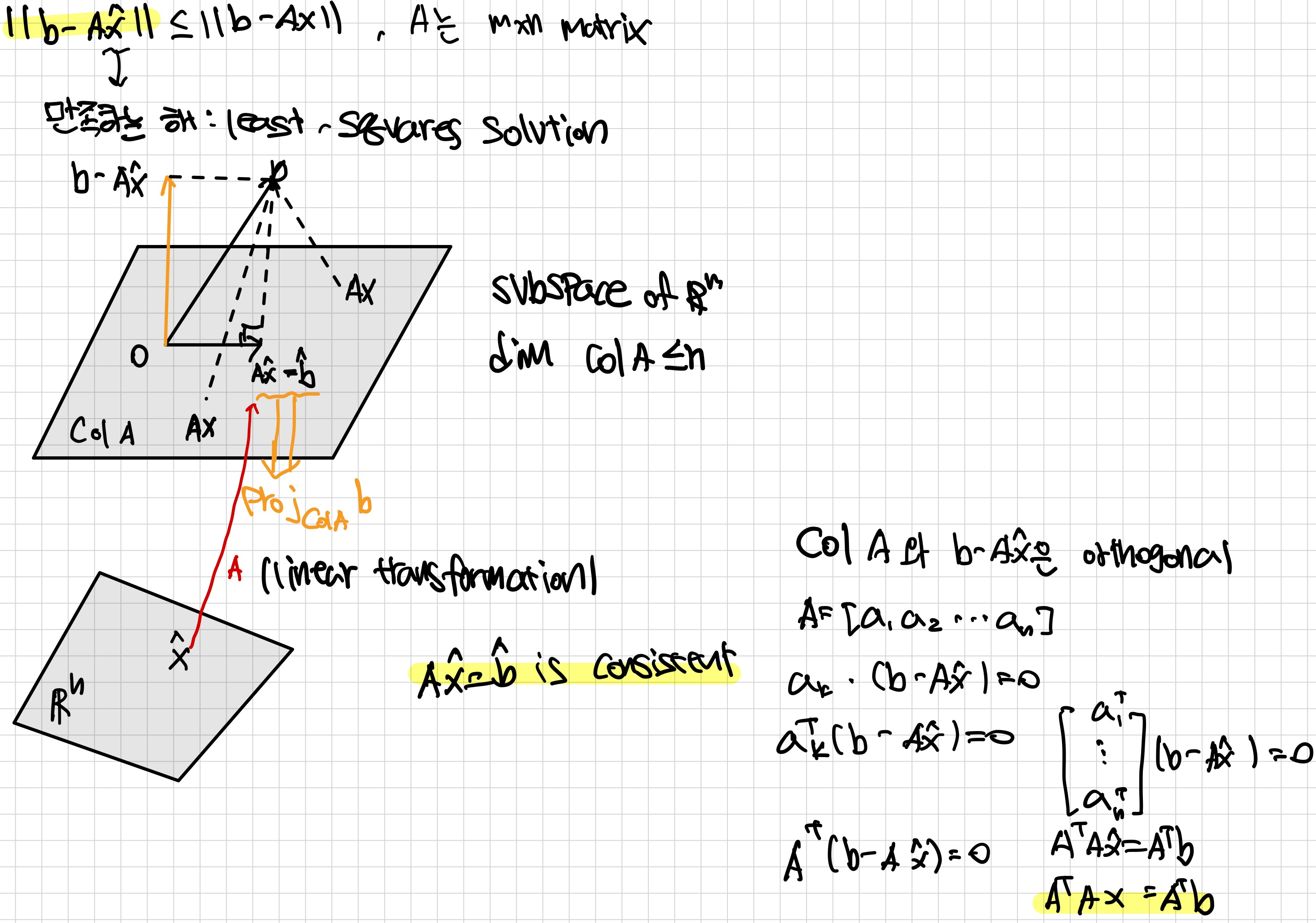
Theorem.

Ax = b의 least-squares solution set은 ATAx = ATb normal equations의 nonempty solution set과 일치하다.

Least-Squares Error

그 외의 증명

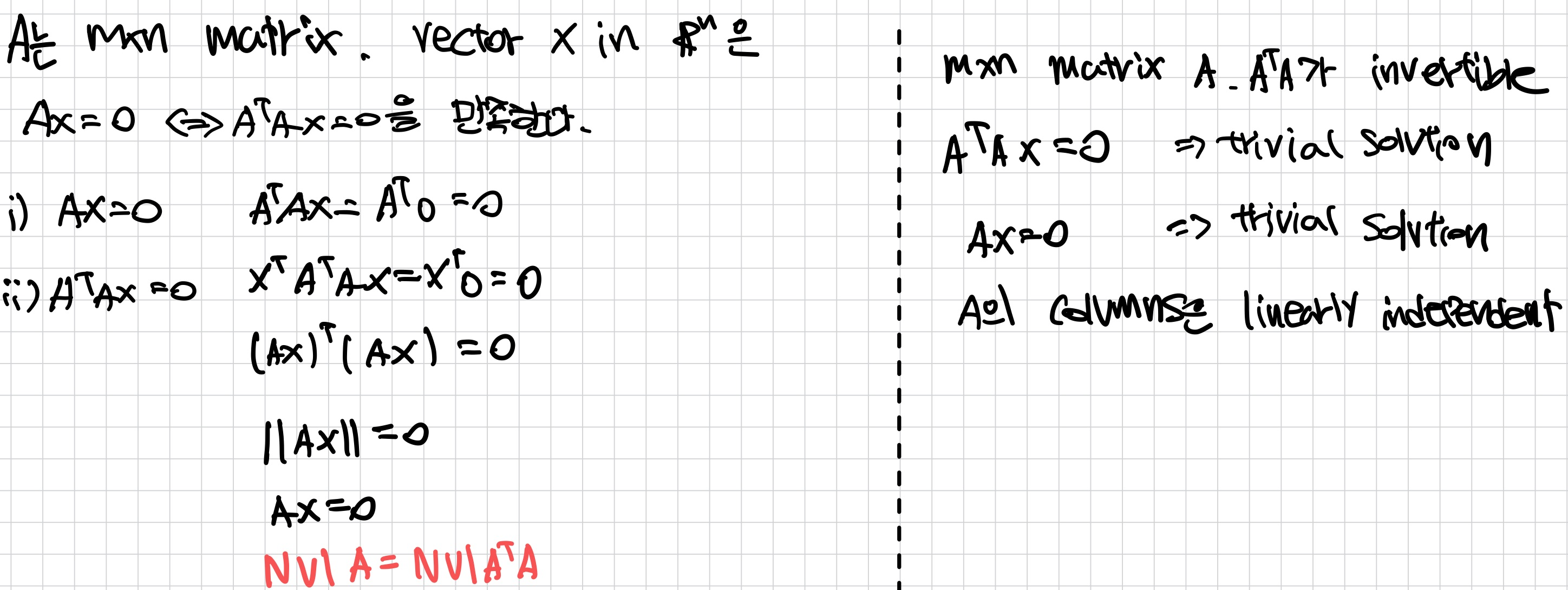
Theorem.

ATA가 invertible과 A의 columns는 linearly independent는 동치이다.

Theorem.

m x n mmatrix A가 linearly independent일 때, A=QR로 factorization이 가능하다. Ax=b equation은 unique least-squares solution을 갖는다.

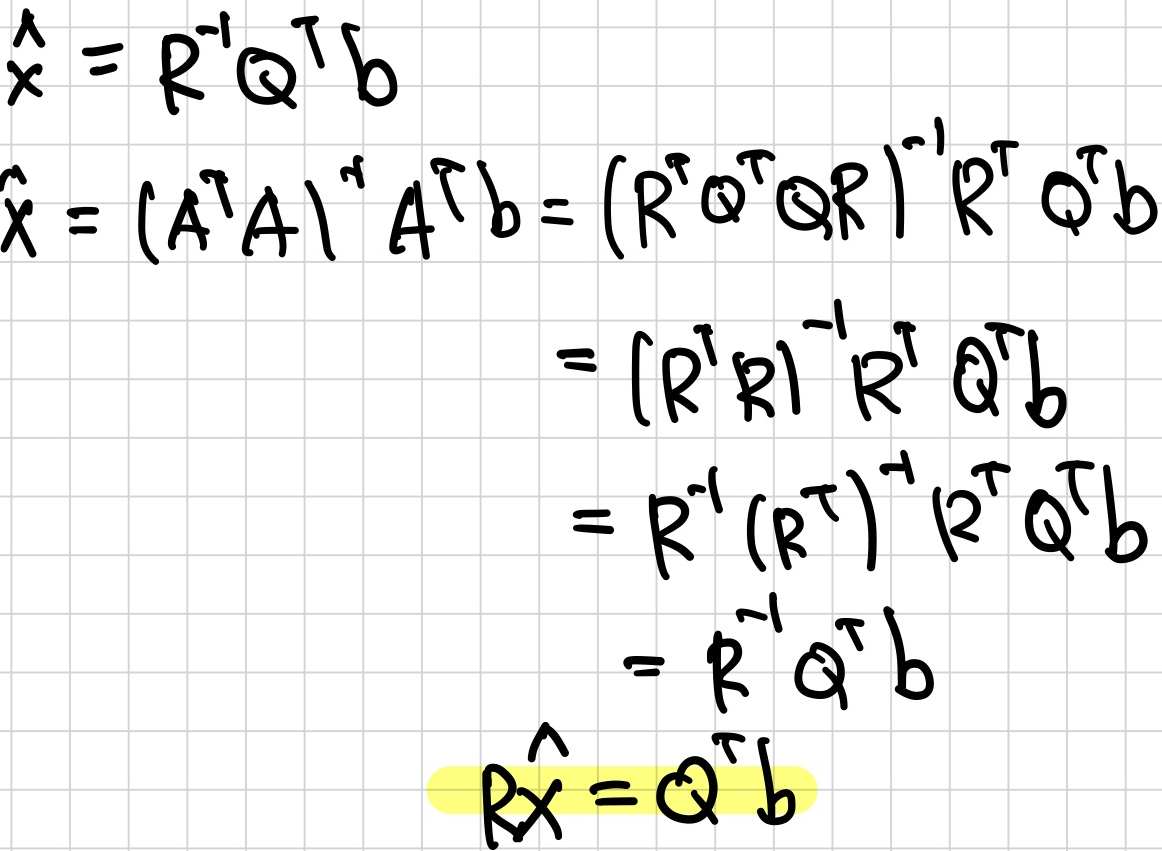
Least-squars fitting

Weighted Least-Squares

• weight를 두어 가중치를 조정