[알고리즘][DFS] DFS

DFS

DFS 알고리즘은 Depth-First Search의 줄임말로 깊이 우선 탐색이라고 부르며, 그래프에서 깊은 부분을 우선적으로 탐색하는 알고리즘이다.

그래프는 노드(Node) = 정점(Vertex)와 간선(Edge)으로 표현된다.

DFS 알고리즘에서는 주로 스택(Stack)과 재귀 함수가 주로 사용된다.

---

스택

스택(Stack)이란 선입후출(First In Last Out) 또는 후입선출(Last In First Out) 구조를 나타낸다.

python에서는 기본 자료형인 list를 통해 나타낸다.

stack = []

stack.append(1)		# [1]
stack.append(2)		# [1, 2]
stack.pop()			# [1]
stack.append(3)		# [1, 3]
stack.append(4)		# [1, 3, 4]
stack.append(5)		# [1, 3, 4, 5]
stack.pop()			# [1. 3. 4]

print(stack)

# 출력 결과
# [1, 3, 4]

---

재귀 함수

재귀 함수란 자기 자신을 다시 호출하는 함수를 말한다.

아래의 코드를 보자.

# 반복 방식
def factorial_iterative(n):
    result = 1
    for i in range(1, n+1):
        result *= i
    return result
    
# 재귀 방식
def factorial_recursive(n):
    if n <= 1:
        return 1
    return n * factorial_recursive(n-1)
    
print(factorial_iterative(5))
print(factorial_recursive(5))

# 출력결과
# 120
# 120

재귀 함수 코드에서 factorial_recursive 함수는 제일 처음 함수를 실행할 때(n=5)부터 재귀적으로 n=1이 될 때까지 총 5번 호출 되었다.

최종적으로 5!의 연산 결과인 120이 반환되었지만, 아래와 같이 코드를 바꿔보면

def factorial_recursive(n):
	print(f"함수 호출됨 n = {n}")
    if n <= 1:
        print(f"계산 완료됨 result = 1")
        return 1
    result = n * factorial_recursive(n-1)
    print(f"계산 완료됨 result = {result}")
    return result
    
print(factorial_recursive(5))

# 출력 결과
# 함수 호출됨 n = 5
# 함수 호출됨 n = 4
# 함수 호출됨 n = 3
# 함수 호출됨 n = 2
# 함수 호출됨 n = 1
# 계산 완료됨 result = 1
# 계산 완료됨 result = 2
# 계산 완료됨 result = 6
# 계산 완료됨 result = 24
# 계산 완료됨 result = 120
# 120

연산 과정이 스택과 유사하다는 것을 알 수 있다.

이러한 성질을 사용해 위 팩토리얼 예시처럼 스택을 사용하지 않고도 스택을 사용하는 것과 유사한 효과를 낼 수 있다.

---

코드

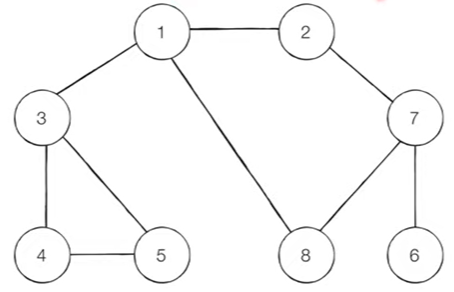
위 그림에서 각각의 노드를 연결된 다른 노들를 기준으로 코드로 표현하면 아래와 같이 나타낼 수 있다.

[
    [],			# 노드가 1번부터 시작되므로 0번에 빈 값을 넣어준다.
    [2, 3, 8],
    [1, 7],
    [1, 4, 5],
    [3, 5],
    [3, 4],
    [7],
    [2, 6, 8],
    [1, 7]
]

이것을 DFS로 풀어보면 다음과 같다(숫자가 낮은 노드를 우선적으로 탐색한다).

def dfs(graph, n, visited):
    visited.append(n)
    for i in graph[n]:
        if i not in visited:
            dfs(graph, i, visited)
    return visited

graph = [
    [],		# 노드가 1번부터 시작되므로 0번에 빈 값을 넣어준다.
    [2, 3, 8],
    [1, 7],
    [1, 4, 5],
    [3, 5],
    [3, 4],
    [7],
    [2, 6, 8],
    [1, 7]
]

print(dfs(graph, 1, []))

# 출력 결과
# [1, 2, 7, 6, 8, 3, 4, 5]