[알고리즘/복잡도] 복잡도와 빅-오 표기법

0. 🔖 목차

---

1. 알고리즘에서 복잡도를 사용하는 이유
2. 시간 복잡도
   2-1. 빅-오(Big-O) 표기법
   2-2. 빅-오(Big-O) 표기법의 수학적 의미
   2-3. 빅-오(Big-O) 사용법
3. 공간 복잡도
   3-1 공간 복잡도의 구성

1. 알고리즘에서 복잡도를 사용하는 이유

---

차를 사기위해 서로 다른 목적을 가진 두 사람이 있다고 하자.

한 사람은 트랙을 달릴 수 있는 차를 사길 원하고, 다른 사람은 패밀리카를 원한다.

트랙에서 달릴 수 있으려면 속력은 빠르고 크기는 작은 차가 필요하며 가족을 위한 차는 속력은 느리고 크기는 큰 차가 필요하다.

이 두 사람은 자신이 원하는 목적의 차를 사기 위해 차의 최고 시속과 크기를 나타낸 지표를 보고 선택할 것이다.

알고리즘도 마찬가지다. 우리가 원하는 작업, 예를 들어 대규모 트래픽 처리용으로 사용할 알고리즘을 선택하려면 속도가 빠른 알고리즘을 선택해야 하고 개발자는 각 알고리즘의 시간복잡도라는 지표를 보며 시간 복잡도가 제일 작은 알고리즘을 채택할 것이다.

이처럼 상황에 맞게 사용할 수 있는 여러 알고리즘의 성능을 비교하기 위해 복잡도라는 지표가 사용되며, 소요 시간을 나타내는 지표인 시간 복잡도와 소요 메모리를 나타내는 지표인 공간 복잡도로 나누어져 있다.

2. 시간 복잡도

---

알고리즘이 입력 크기에 따라 얼마나 빠르게 실행되는지를 나타내는 지표.
일반적으로 Big O 표기법을 사용하여 나타내며, 최악의 경우에 대한 상한을 제공한다.

2-1. 빅-오(Big-O) 표기법

차량을 구매하려고 스펙을 비교하는데 속도: "빨라용", 크기: "커용" 이런식으로 되어있으면 지표라고 할 수 없다.

알고리즘도 마찬가지로 빠름, 느림으로 표시할 순 없기 때문에 위 그림처럼 빅-오라는 표기법을 사용하여 구체적으로 나타내기로 약속했다.

빅오 표기법은 알고리즘의 실행 시간이나 공간 사용량이 입력의 크기에 따라 어떻게 증가하는지를 표현한다.

여기서 $n$은 입력의 크기를 나타내며 $O(n)$이라고 표시되어있으면 "이 알고리즘은 소요 시간이 입력의 개수 $n$에 대해서 선형적으로 증가한다!"라고 해석하면 된다.

2-2. 빅-오(Big-O) 표기법의 수학적 의미

내용이 너무 길어서 따로 정리함.

수학적 정의

위 정의의 의의와는 약간 벗어났지만 알기 쉽고 저렴하게 설명하자면 아래와 같다.

$n$이 겁나게 크면 $n^4+2n^3-4n+9$ 이거나 $n^4$ 이거나 또이또이니까
그냥 $n^4$이라고 표현하자!

실제로 그런지 확인해보자

그래프에서 보이듯 $g(n)$에 대한 $f(n)$의 비율이 발산하지 않고 수렴하는 것을 볼 수 있다. 이는 $n$이 커질수록 $g(n)$이 $f(n)$에 점진적으로 근사한다는 의미이다.

실제로 n이 충분히 큰 경우인 $n = 1000000$ 일 때 $h(n)$은 $1.000002$정도이다.
이는 $n = 1000000$이면 빅-오 표기법으로 표기한 값이 실제값과 고작 0.0002%의 오차라는 뜻이다.

따라서 어떤 알고리즘의 입력 $n$에 대해 걸리는 소요 시간을 표기하기 위해서 $n^4+2n^3-4n+9$라고 쓰지 않고 $O(n^4)$라고 단순화하여 표시할 수 있으며 이것이 알고리즘에서 빅-오 표기법의 존재 이유다.

공식적인 정의를 알고 싶으면 앞서 언급한 수학적 정의를 보는걸 추천, 최대한 쉽게 설명했다.

2-3. 빅-오(Big-O) 사용법

사실 다 필요없고 아래 두 개만 외우면 된다.

1. 최악의 경우를 고려: 빅오는 주로 최악의 경우에 대한 상한을 표현한다.

2. 상수항 무시: 빅오 표기법에서는 상수항이나 낮은 차수의 항을 무시한다. 예를 들어, $O(2n)$은 $O(n)$으로 표현되며, $O(3n^2 + 2n + 1)$은 $O(n^2)$으로 간소화한다.

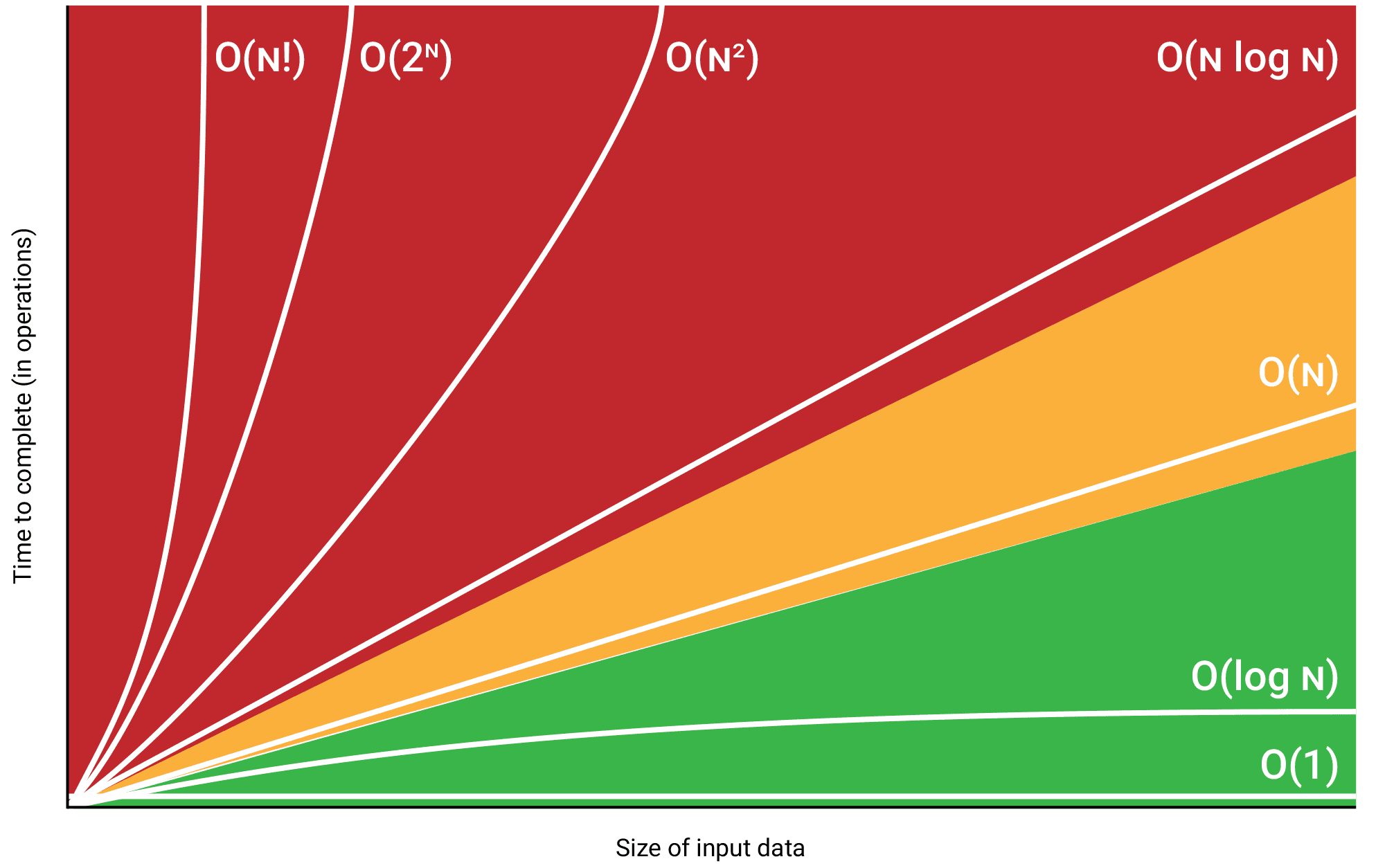
아래는 몇가지 빅-오 표기법에 대한 설명과 그래프다. 그래프를 참고하여 각 표기법의 대소관계를 알아두자

• $O(1)$ - 상수 시간 복잡도: 입력 크기와 무관하게 일정한 실행 시간이 소요
• $O(log n)$ - 로그 시간 복잡도: 입력 크기에 대해 로그 증가하는 시간 복잡도
• $O(n)$ - 선형 시간 복잡도: 입력 크기에 비례하여 선형으로 증가하는 시간 복잡도
• $O(n^2)$ - 이차 시간 복잡도: 입력 크기의 제곱에 비례하여 증가하는 시간 복잡도
• $O(n!)$ - 팩토리얼 시간 복잡도: 입력 크기의 팩토리얼에 비례하여 증가하는 시간 복잡도

$O(2^n)$의 시간 복잡도를 가진 알고리즘에 크기가 10인 입력을 넣으면 1024번의 계산을 한다는 결과가 나온다. 그럼 1024초가 걸린다는 건가? 1024분이 걸린다는건가?

빅-오 표기법은 소요되는 시간의 정량적인 값을 중점으로 보는게 아니다.

이 알고리즘이 입력의 크기에 따른 소요 자원이 어떠한 형태로 증가하는지, 다른 알고리즘과의 자원 소모를 비교하면 어느정도인지를 파악하는게 주 목적이다.

따라서 $O(2^n)$의 시간 복잡도를 가진 알고리즘을 본다면 "이 알고리즘은 입력에 대해서 지수적으로 증가하는 알고리즘이구나, 대용량 데이터를 처리할때 사용하면 안되겠어."와 같이 판단하는게 좋다.

3. 공간 복잡도

---

공간 복잡도는 알고리즘이나 프로그램이 얼마나 많은 메모리를 사용하는지를 나타내는 지표이다. 시간 복잡도와 마찬가지로 빅-오 표기법을 사용한다.

3-1. 공간 복잡도의 구성

나는 맨 처음에 "데이터 $n$개를 처리하려면 무조건 데이터 $n$개가 메모리에 올라와 있긴 해야하니까 공간 복잡도는 최소 $O(n)$이어야 하는거 아냐?" 라고 생각했는데 아니다.

공간 복잡도는 고정 공간과 가변 공간의 합으로 나타내는데

• 고정 공간(알고리즘과 무관한 공간)
  - 코드 저장 공간, 단순 변수 및 상수
• 가변 공간(알고리즘 실행과 관련있는 공간)
  - 실행 중 동적으로 필요한 공간

보통 공간 복잡도를 빅-오로 표기할 때는 저 가변 공간을 나타내는 것 같다. 내가 앞서 생각한 알고리즘을 적용할 데이터 그 자체는 고정 공간에 포함된 데이터인듯(확실하지 않음,,, 나중에 수정할 예정)

예를 들어 버블 정렬을 하기 위해 길이가 $100000$인 배열을 입력으로 준다면
고정 공간은 $100000$ 즉 $O(1)$, 가변 공간은 $O(1)$이 된다.

버블 정렬을 하는 동안에는 많아봐야 변수 몇개를 선언하는 것 말고는 더 필요하지 않기 때문

def fact(x):
	if x <= 0: 
    	return 1
    else:
		n = x*fact(x-1)
		return n

반면에 팩토리얼을 구하기 위한 재귀 알고리즘에서 입력으로 $1000$이 들어갔다면 재귀로 인해 아래 코드의 변수 n이 $1000$개 더 필요하게 되므로 $O(n)$이 된다.

def fact(x):
	tmp = 1
	for i in range(1,x+1):
    	tmp *= i
    return tmp

근데 만약 팩토리얼을 재귀가 아니라 반복문을 통해서 구한다고 하면 $O(1)$이 된다. 변수가 i 밖에 필요하지 않고 같은 i 변수에 다른 값이 대입되기 때문이다.