[알고리즘/복잡도] 빅-오(Big-O)표기법의 수학적 의미

0. 🔖 목차

---

1. 수학적 정의
2. 첫 번째 정의
3. 세 번째 정의

1. 수학적 정의

---

위 그림은 위키백과에서 찍어온 빅-오 표기법에 대한 정의이다. 이렇게만 보면 무슨 말인지 이해가 안간다. 천천히 알아보자

2. 첫 번째 정의

---

충분히 큰 모든 $x>x_0$에 대해 $|f(x)<M|g(x)|$가 성립한다는 것은 $|g(x)|$ 함수에 상수 $M$을 곱한 값은 $x$가 어떤 점($x_0$) 이상부터 $|f(x)|$의 값을 항상 상회한다는 뜻이고 첫번째 정의는 이러한 $M$과 $x_0$가 존재한다는 뜻이다.

백문이 불여일견이니 직접 예시를 들어보자.

$f(x)=2x^2-6x+1$
$g(x)=x$
$M=10$

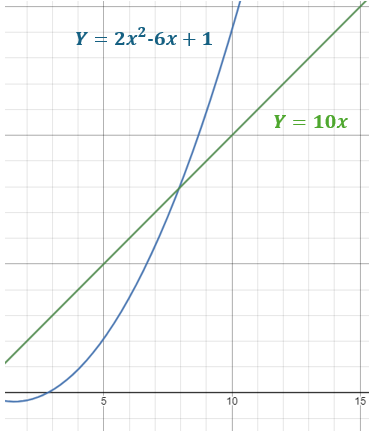
위 경우를 생각해보자

$x_0$를 대충 3정도라고 했을 때 $g(x)$의 절대값에 $M$을 곱한 결과(그림에서 초록색 그래프)가 모든 $x>x_0$인 $x$에 대해서 $|f(x)|$보다(그림에서 파란색 그래프) 위에 있는가?

약 $x=8$정도 부터 성립하지 않는걸 확인할 수 있다. $M$을 계속 키워서 초록색 그래프의 기울기를 올려도, $x_0$를 음수가 아닌 어느 부분에 놓아도 증가율이 다르기 때문에 언젠가는 파란색 그래프가 추월하는 부분이 생긴다.

즉 $g(x)=x$라고 했을 때 이를 만족하는 $M$과 $x_0$가 존재하지 않으므로 $f(x)=O(x)$라고 표기할 수 없다.

$f(x)=2x^2-6x+1$
$g(x)=x^2$
$M=2$

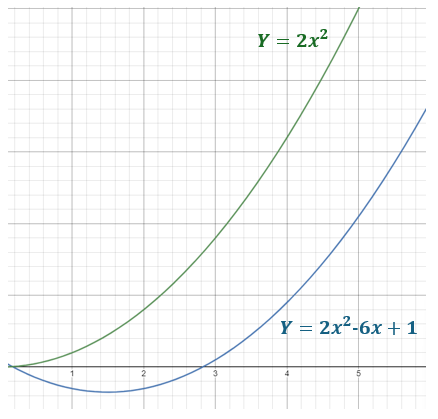
이번엔 위 경우를 생각해보자

$x_0$를 어림잡아 3정도라고 해도 $g(x)$의 절대값에 $M$을 곱한 결과(그림에서 초록색 그래프)가 모든 $x>x_0$인 $x$에 대해 $|f(x)|$보다(그림에서 파란색 그래프) 위에 있다.

증가율이 같기 때문에 상수배만 해도 추월당하지 않는 것이다.

즉 $g(x)=x^2$이라고 했을 때,
이를 만족하는 $M$과 $x_0$가 존재하므로 $f(x)=O(x^2)$라고 표기할 수 있다!

$f(x)=2x^2-6x+1$
$g(x)=x^3$
$M=0.2$

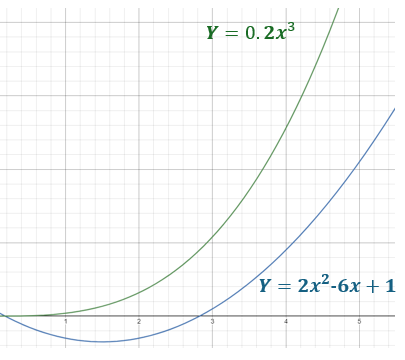
위 경우도 생각해보자

이젠 $M$이 0.2만 되어도 조건을 만족한다.

$x^3$증가율이 $x^2$의 증가율보다 높기 때문이다.

즉 $g(x)=x^3$이라고 했을 때,
이를 만족하는 $M$과 $x_0$가 존재하므로 $f(x)=O(x^3)$이라고도 표기할 수 있다.

지금까지의 내용을 모두 정리해봤을 때 $f(x)=2x^2-6x+1$에서 빅-오 표기법으로 나타낼 수 있는 $g(x)$는 $x^2$, $x^3$, $x^4$, $x!$, $2^x$, ... 등등 무수히 많을 것이다.

그래서 $f(x)=O(g(x))$라고 하면 문제가 생긴다.
하나의 $f(x)$에 여러 $O(g(x))$가 있을 수 있기 때문이다(vice-versa).
따라서 이를 집합으로 여기며 $f(x)∈O(g(x))$라고 표기하기도 한다.

3. 세 번째 정의

---

세 번째 부분도 첫 번째 부분과 같은 의미다. 세 번째 부분을 쉽게 설명하자면
$limsup_{x->a}|f(x)/g(x)|<∞$는 $x$가 $a$에 접근할 때,
$g(x)$에 대한 $f(x)$의 비율이 발산하지 않음을 의미한다.

g(x)가 f(x)와의 증가율이 같거나 보다 높다면(다항식의 경우, 최고차항의 차수가 같거나 더 높다면) 위 비율은 특정 값으로 수렴(같은 경우)하거나 0으로 수렴(높은 경우)한다.

즉, 발산하지 않기 때문에 세번째 부분을 만족하므로 $f(x)$보다 증가율이 같거나 높은 $g(x)$는 $f(x)$에 대한 빅-오 표기법으로 사용 가능하다.

다항식에서 최고차항을 언급한 이유는 보통 다항식에서 증가율을 지배하는 것은 최고차항이기 때문이다.

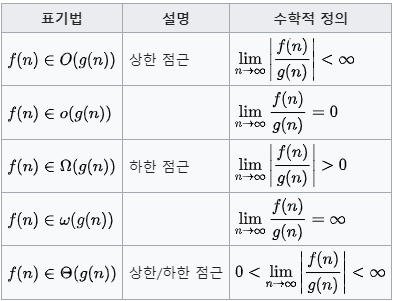
이를 감안하여 위 정의를 보면 나머지 기호들도 이해하기 쉬워진다.

• 빅-오의 경우 $f(n)$보다 증가율이 높거나 같은 $g(n)$을 사용해야 한다.

  따라서 $f(n)=O(g(n))$라고 되어있으면 "아 $f(n)$의 증가율이 아무리 커봤자 $g(n)$정도거나 더 작겠구나"라고 이해하면 된다. 그래서 상한 점근이라고 한다.

  통상적으로 알고리즘의 복잡도를 표기할 때 "이 알고리즘은 아무리 증가율이 커봤자(제일 최악의 상황일 때)이정도 증가율이에요"에서 "이정도 증가율"이 위의 맥락과 일치하기 때문에 알고리즘에서 빅-오 표기법을 사용한다.

• 리틀-오의 경우 $f(n)$보다 증가율이 높은 $g(n)$을 사용해야 한다.

• 빅-오메가의 경우 $f(n)$보다 증가율이 낮거나 같은 $g(n)$을 사용해야 한다.

  따라서 $f(n)=Ω(g(n))$라고 되어있으면 "아 $f(n)$의 증가율이 아무리 작아봤자 $g(n)$ 정도거나 더 크겠구나"라고 이해하면 된다. 그래서 하한 점근이라고 한다.

  알고리즘에서 최선의 경우를 표현할 때 "이 알고리즘은 아무리 증가율이 작아봤자(제일 최선의 상황일 때)이정도 증가율이에요"에서 "이정도 증가율"이 위의 맥락과 일치하기 때문에 알고리즘에서 최선경우 시간 복잡도를 표기할 때 빅-오메가 표기법을 사용한다.

• 리틀-오메가의 경우 $f(n)$보다 증가율이 낮은 $g(n)$을 사용해야 한다.

• 빅-세타의 경우 $f(n)$과 증가율이 같은 $g(n)$을 사용해야 한다.

  따라서 $f(n)=Θ(g(n))$라고 되어있으면 "아 $f(n)$의 증가율은 $g(n)$의 증가율과 같구나"라고 이해하면 된다. 상한 이하, 하한 이상의 모든 $g(n)$의 집합이 여기에 해당될 수 있으며 이때문에 알고리즘에서 평균의 경우를 표현할 때 사용된다.