0. 🔖 목차
- 다익스트라 알고리즘
1-1. 개요
1-2. 알고리즘
1-3. 그림으로 이해하는 다익스트라
1. 다익스트라 알고리즘
1-1. 개요

가중치 그래프에서 특정 노드와 다른 모든 노드들과의 최단 경로를 점진적으로 구해주는 알고리즘이다.
두 개의 노드 사이의 최단 경로를 찾고 싶다면 하나의 노드를 시작으로 다익스트라 알고리즘을 실행한 뒤 다른 하나의 노드의 최단 거리가 확정되면 중단하는 방식으로 최단 경로를 구할 수 있다.
- 초기화: 시작 노드의 거리 값을 0으로 설정하고, 나머지 노드들의 거리 값을 무한대로 설정
- 거리 업데이트: 현재 노드에서 인접한 노드들까지의 거리를 계산(현재 길이 + 노드까지의 거리)하고, 만약 계산한 거리가 기존에 기록한 거리보다 짧다면, 거리 값을 업데이트하면서 우선순위 큐에 저장
- 노드 선택: 아직 방문하지 않은 노드 중에서 계산한 거리 값이 가장 작은 노드를 선택하고, 이 노드를 현재 노드로 변경 후 2를 반복
- 종료 조건: 모든 노드를 방문하거나, 목적지 노드에 도달하면 종료
- 결과: 시작 노드로부터 각 노드까지의 최단 거리와 경로를 제공
1-2. 알고리즘
import heapq # 우선순위 큐를 위한 힙큐 모듈
def dijkstra(graph, start):
# 거리 정보를 저장할 딕셔너리, 무한대로 초기화
distances = {vertex: float('infinity') for vertex in graph}
distances[start] = 0 # 시작 노드의 거리는 0
# 모든 노드를 방문할 때까지의 거리 정보를 우선순위 큐에 저장
priority_queue = [(0, start)]
while priority_queue:
# 가장 짧은 거리를 가진 노드 선택
current_distance, current_vertex = heapq.heappop(priority_queue)
# 이미 방문한 노드는 무시
if current_distance > distances[current_vertex]:
continue
# 인접 노드 거리 업데이트
for neighbor, weight in graph[current_vertex].items():
distance = current_distance + weight
# 더 짧은 경로 발견 시 거리 업데이트 및 큐에 추가
if distance < distances[neighbor]:
distances[neighbor] = distance
heapq.heappush(priority_queue, (distance, neighbor))
return distances
# 간단한 가중치가 있는 방향 그래프 예시
graph = {
'A': {'B': 1, 'C': 4},
'B': {'C': 2, 'D': 5},
'C': {'D': 1},
'D': {}
}
# 'A'에서 시작하여 각 노드까지의 최단 거리 계산
print(dijkstra(graph, 'A'))1-3. 그림으로 이해하는 다익스트라

여기 내 친구 Josh가 있다.
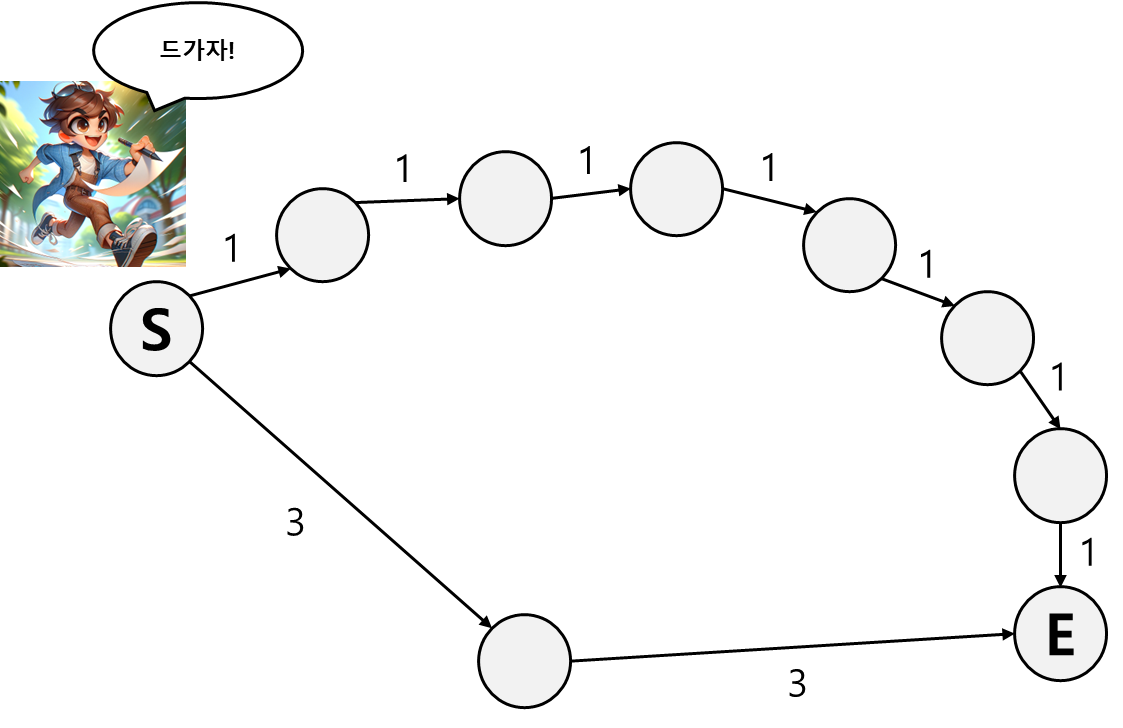
Josh는 S부터 E 까지의 최단 경로를 찾고자 한다.
그리고 이를 찾기 위해 그리디 알고리즘을 사용하려 한다.
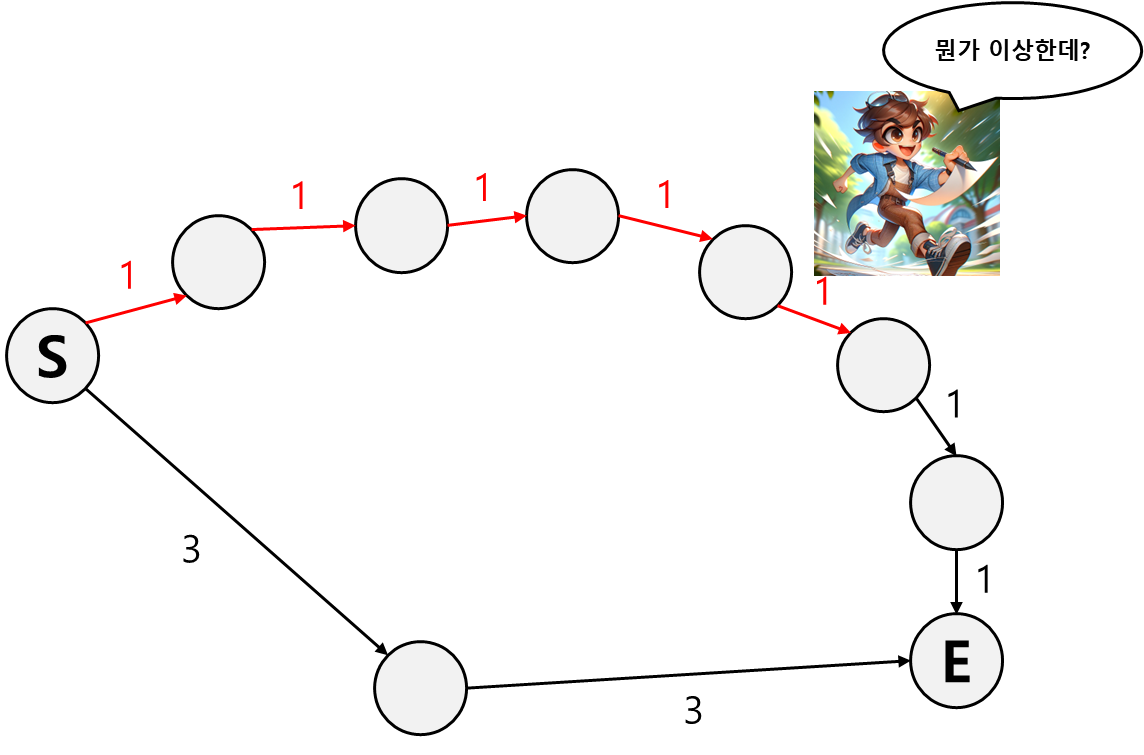
어느정도 도달한 뒤 Josh는 이상한 점을 깨닫게 된다.
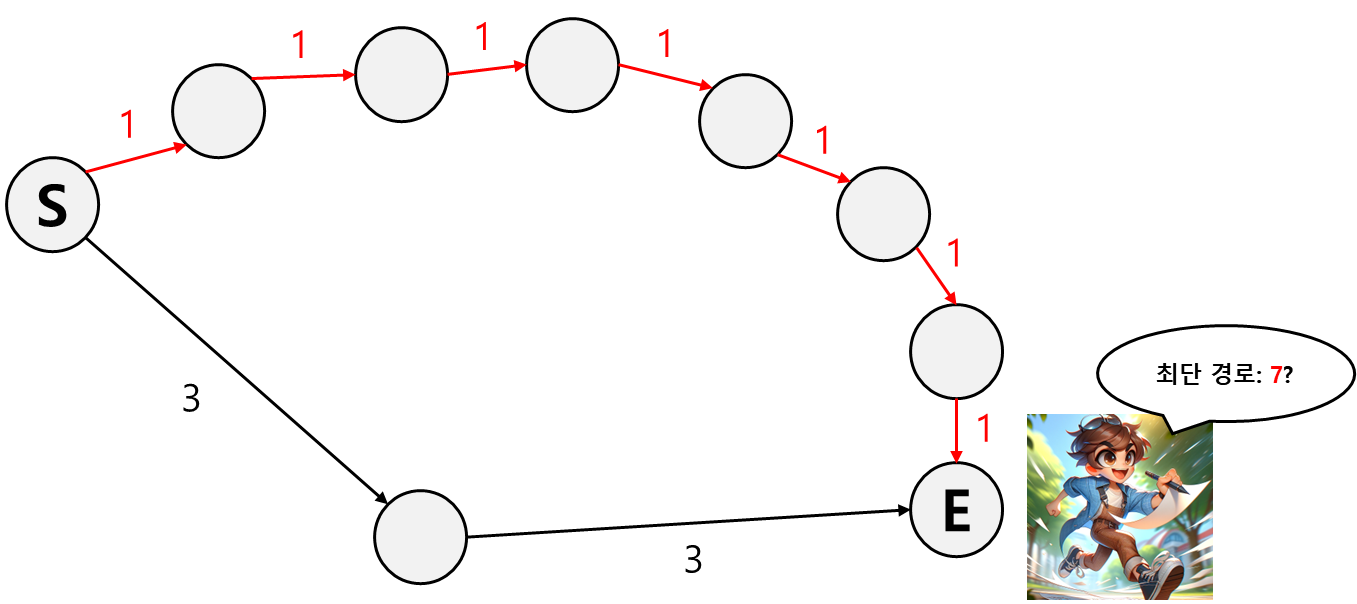
분명 그리디 알고리즘대로 매 순간마다 최단의 경로를 선택해왔는데 옆에 누가봐도 더 짧은 경로가 보인다.
아무래도 그리디 알고리즘만으로는 최단 경로를 찾을 수 없을 것 같다.
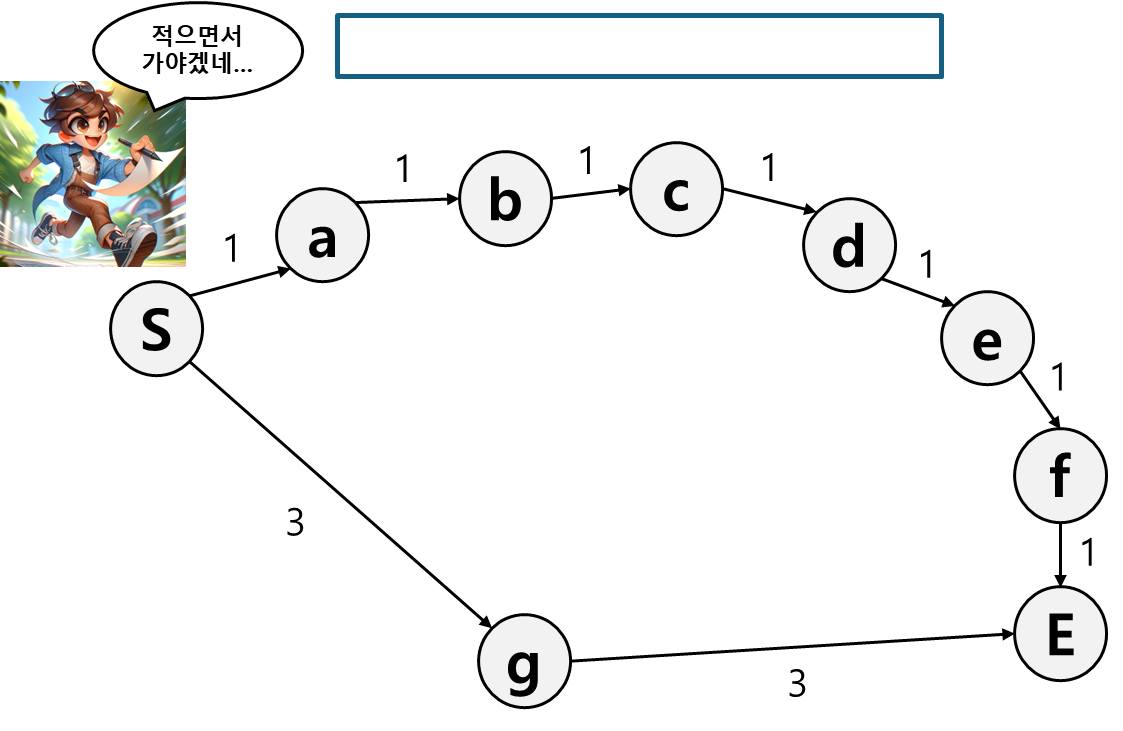
그래서 Josh는 마주치는 분기마다의 경로를 저장하고 최소가 되는 경로만 선택하기로 한다.
우리가 탕후루를 만들기 위해 설탕, 나무 꼬치, 귤을 사려고 쿠팡에 설탕을 검색했다가 그 3개가 다 들어있는 탕후루 밀키트를 보게 되었다면 어떻게 할 것인가?
- 일단 그 탕후루 밀키트의 가격을 "기록"해두고
- 설탕만 샀을 때의 가격과 비교, 밀키트가 더 싸면 밀키트 구매
- 설탕, 나무 꼬치를 샀을 때의 가격과 비교, 밀키트가 더 싸면 밀키트 구매
- 설탕, 나무 꼬치, 귤을 샀을 때의 가격과 비교, 밀키트가 더 싸면 밀키트 구매
현명한 소비자라면 위와 같은 과정으로 진행할 것이다.
Josh가 분기마다 경로를 기록하는 것도 같은 이유다.
- 지금은 더 짧은 경로로 가다가(설탕, 나무 꼬치, 귤을 하나씩 사다가)
- 어느 순간 내가 이전에 기록해둔 경로가 더 짧다면(밀키트가 더 싸다면)
- 그 경로로 가는게 훨씬 이득(밀키트 사는게 더 이득)이라는 것이다
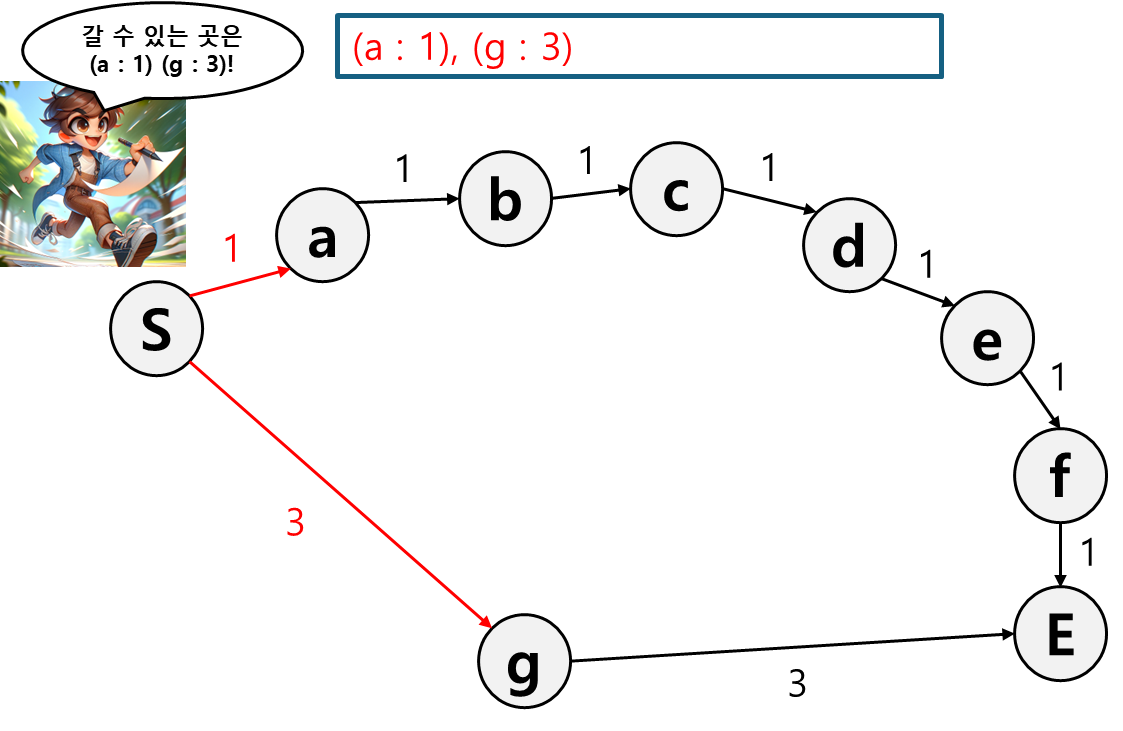
그렇게 첫 분기에서 두 경로를 기록하고
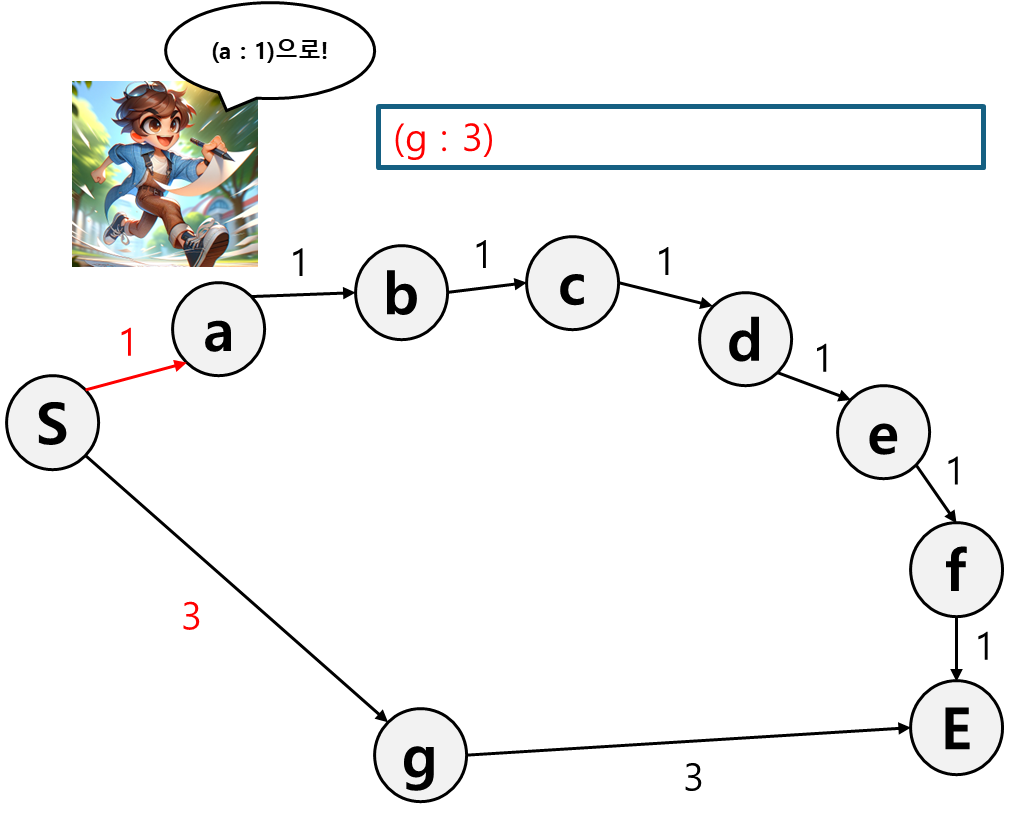
일단은 먼저 짧은 경로를 선택한다.
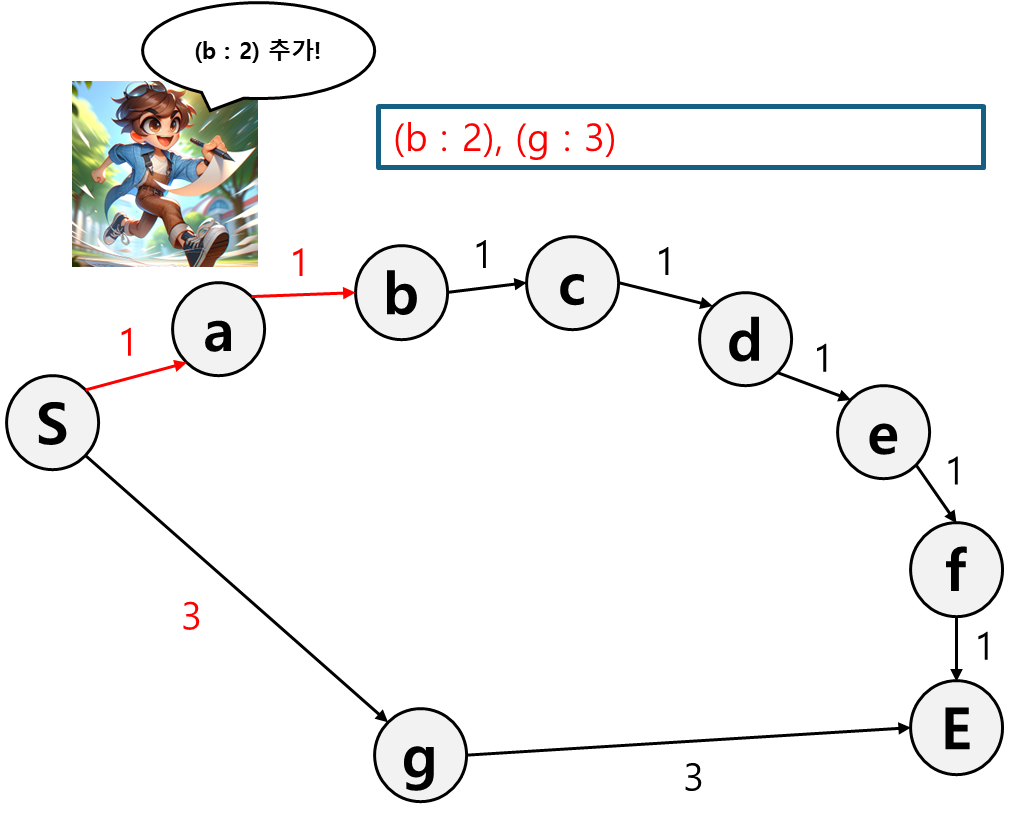
현재 분기는 b로 가는 경로밖에 없으니 b로 가는 경로의 비용을 기록한다.
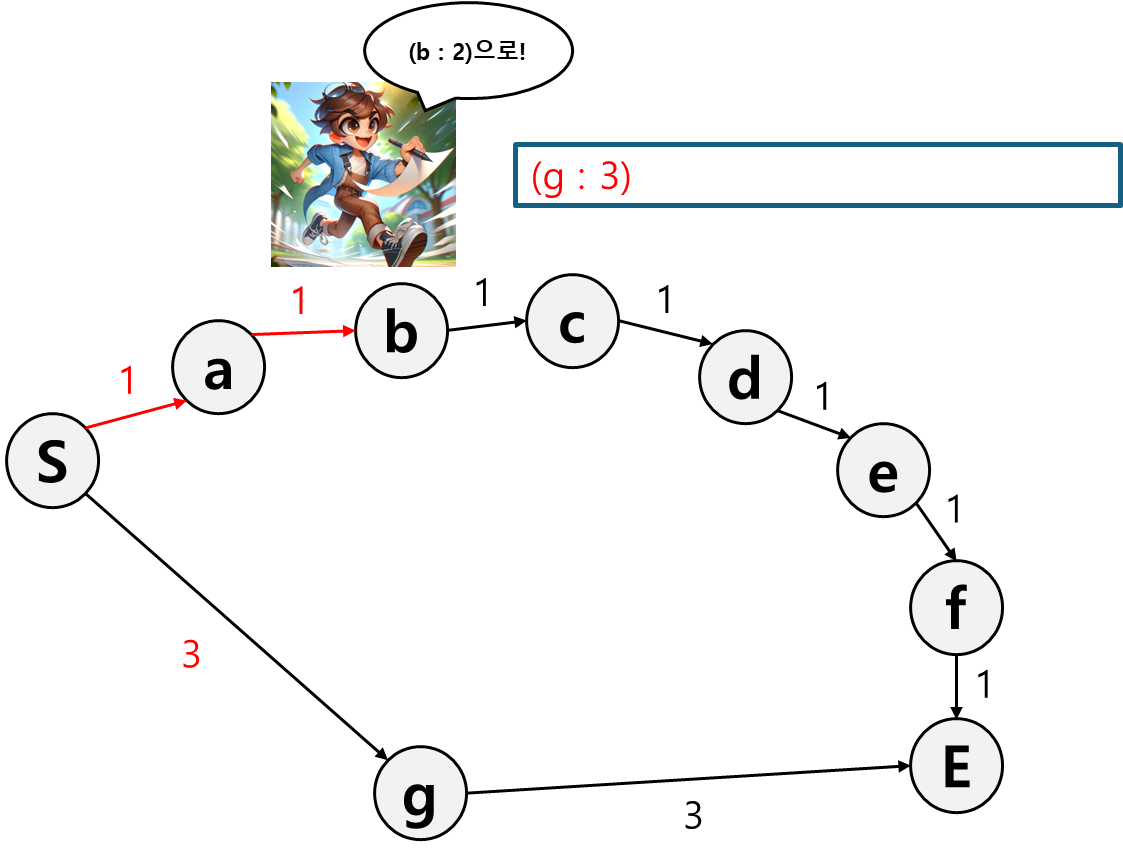
아직까진 b로 가는게 g로 가는거보다 싸니까 b로 간다.
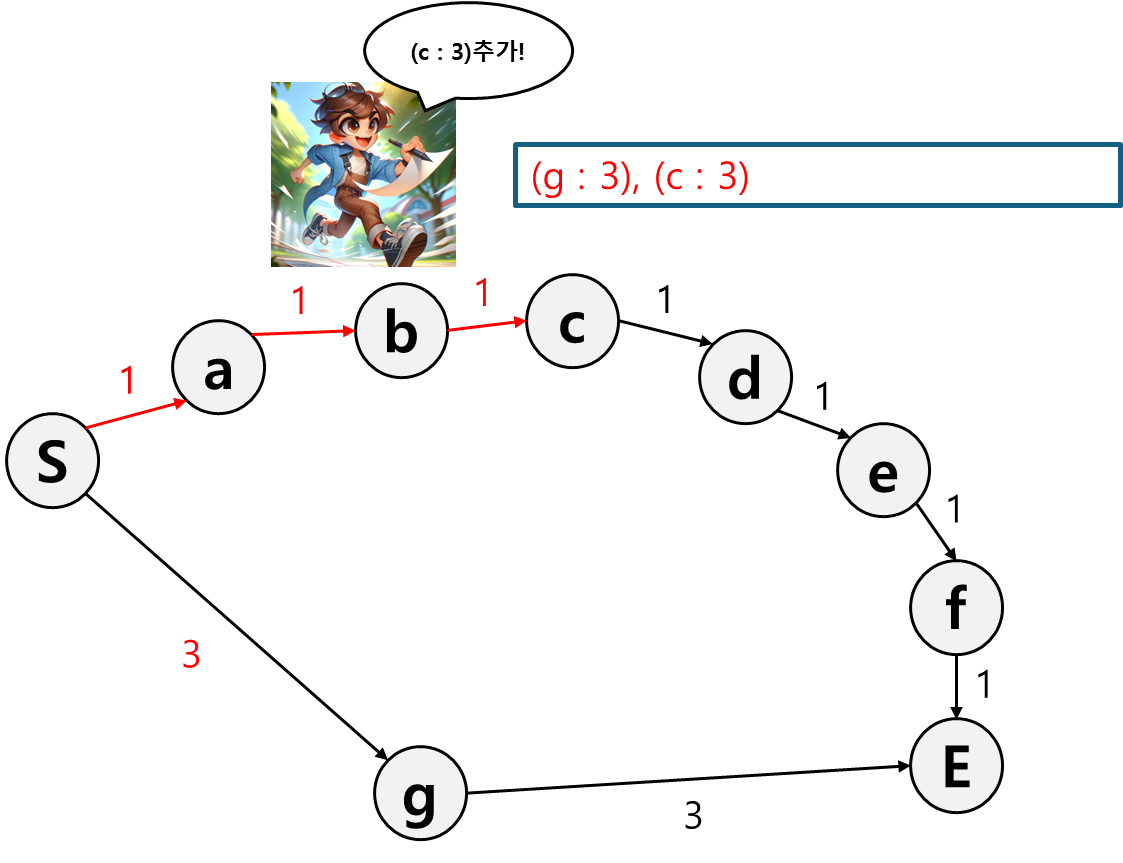
c 경로의 비용을 추가해준다.
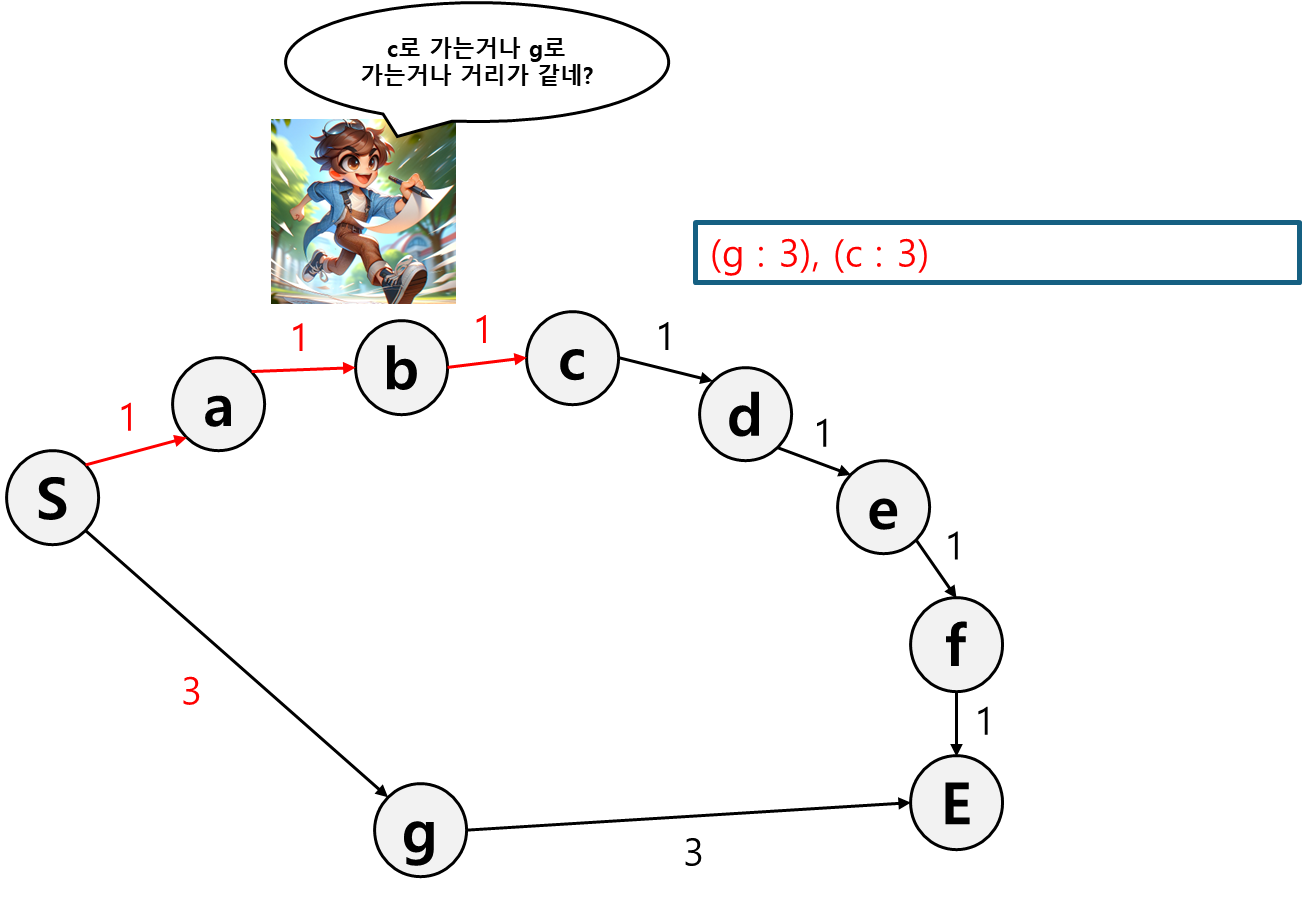
이제는 c로 가는 것이나 g로 가는 것이나 비용이 같아졌다.
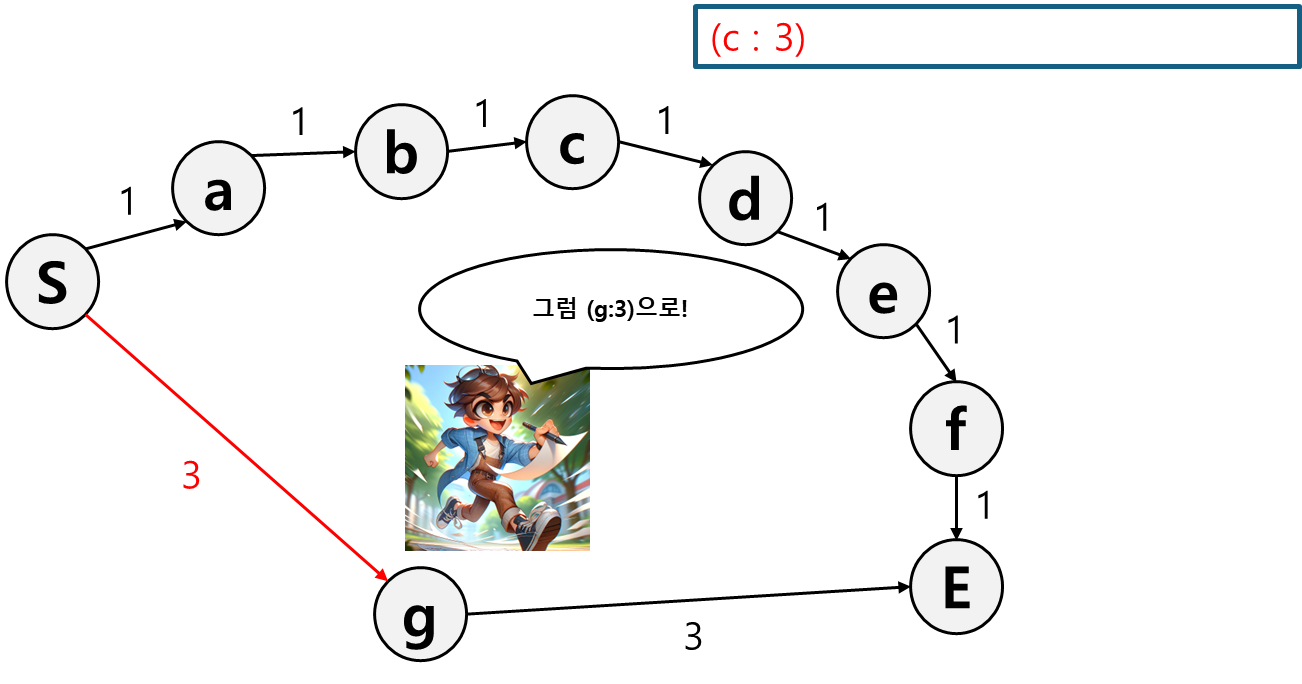
앞서 먼저 기록해뒀던 g로 이동한다.
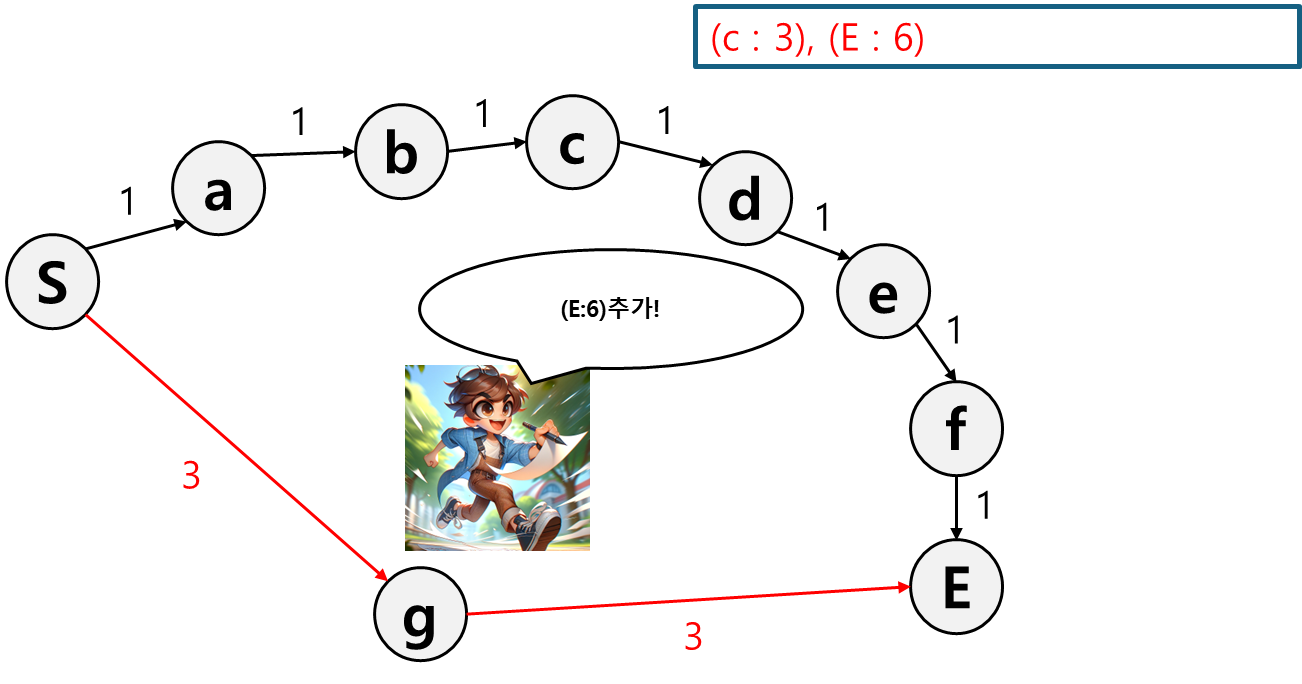
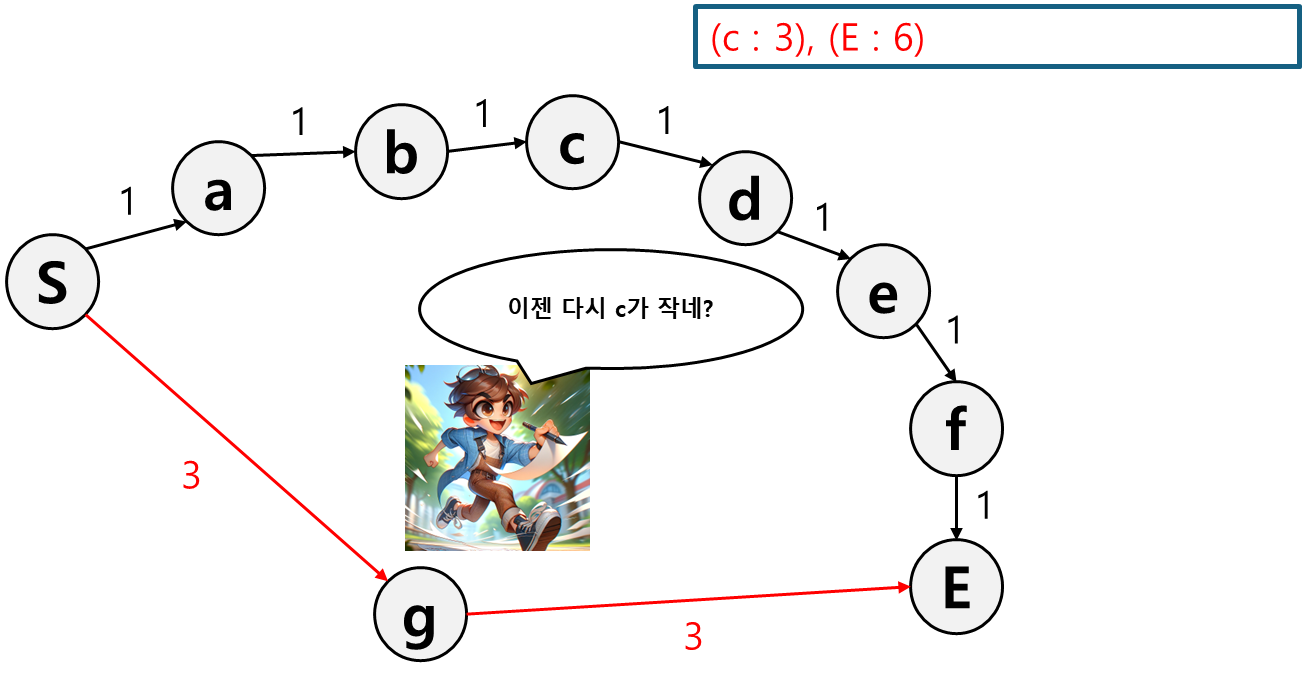
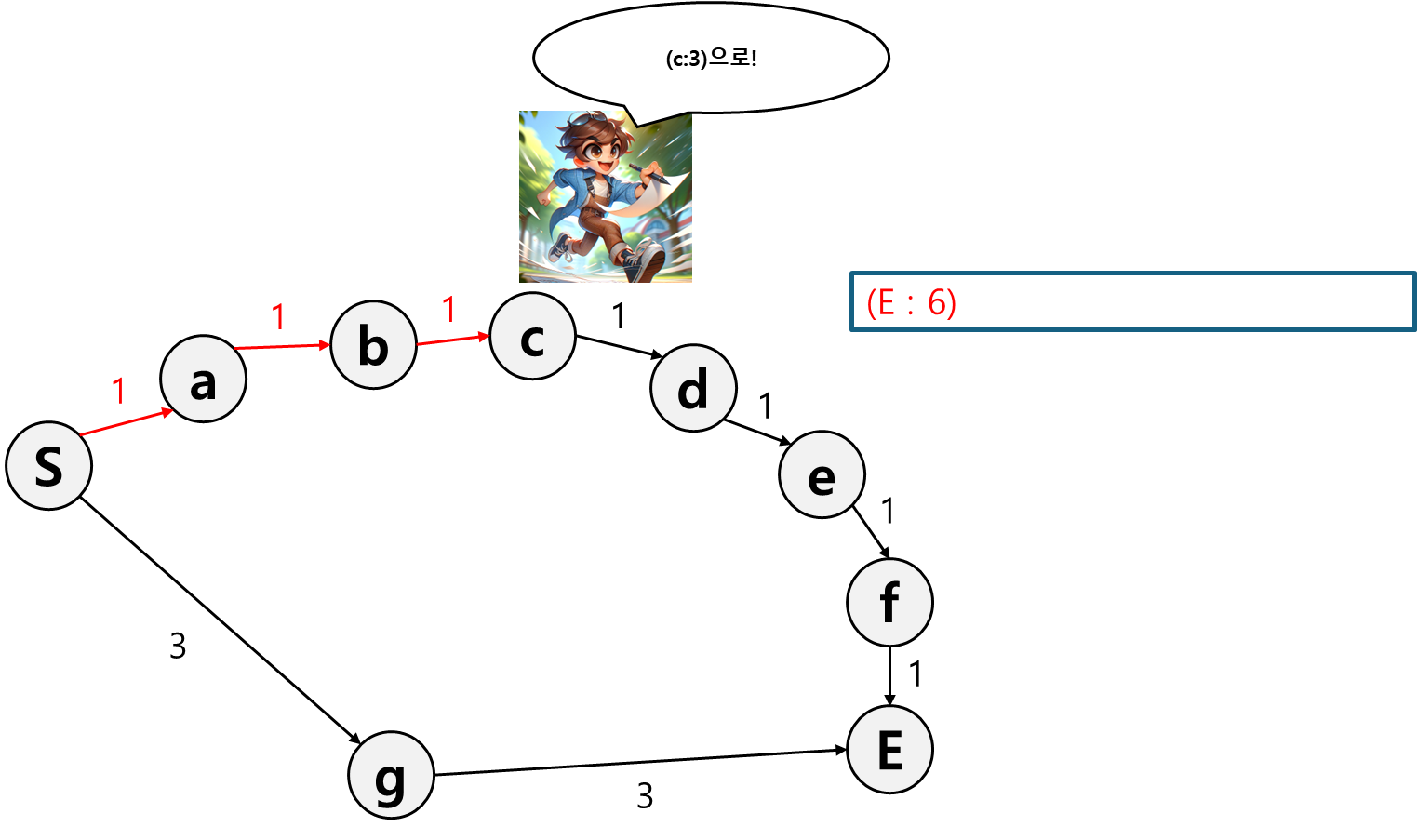
E 경로를 기록했더니 이번엔 c가 제일 작다. 그러니 c로 이동한다.
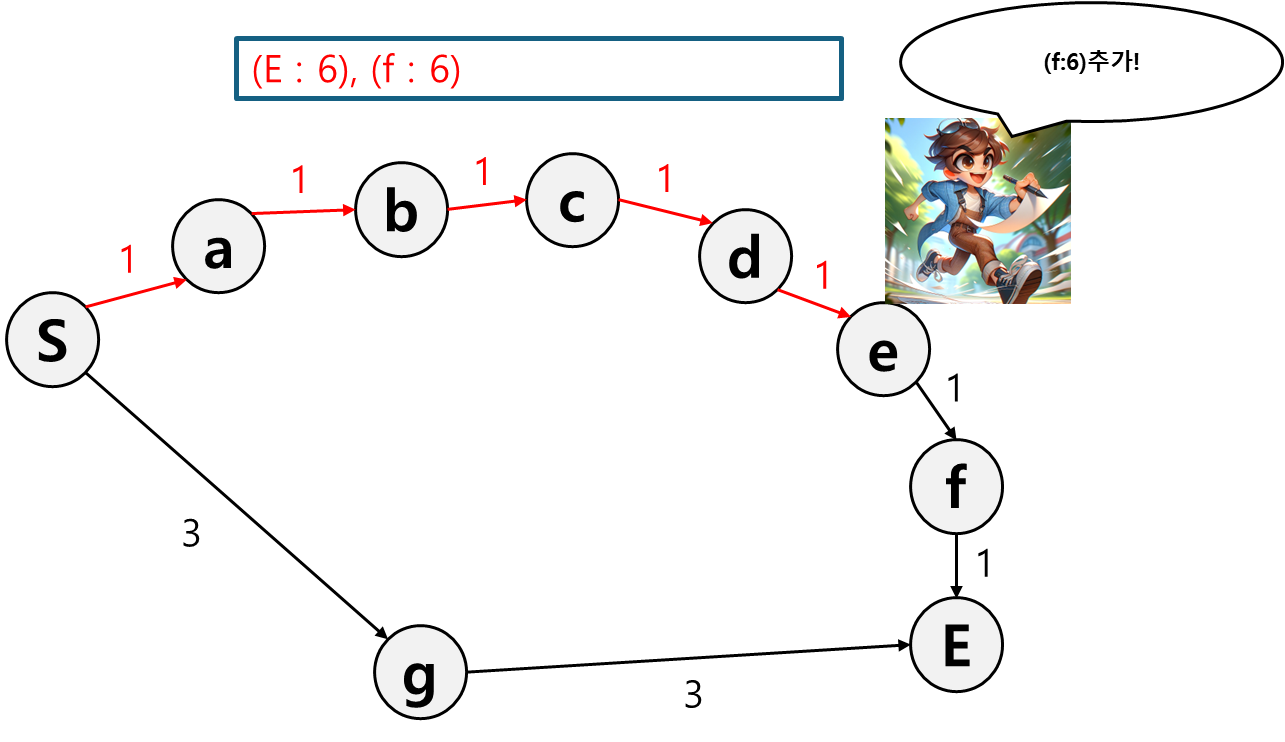
그렇게 쭉 가다가 f 경로를 추가하려 할 때 E 경로와 길이가 같기 때문에 먼저 기록해 두었던 E 경로로 진행한다.
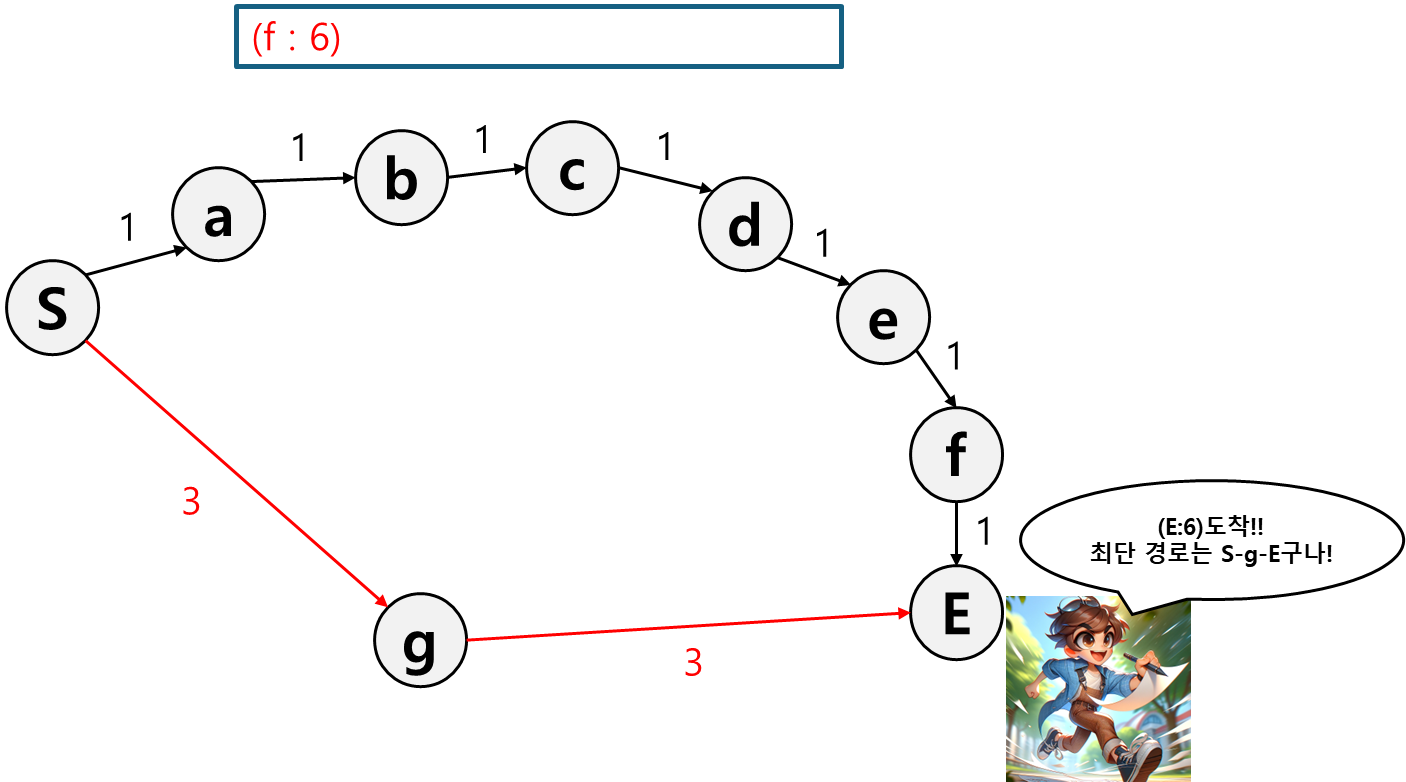
이렇게 Josh는 최단 경로를 찾을 수 있었다.
이 과정이 바로 다익스트라 알고리즘의 동작 방식이고 Josh가 기록했던 리스트(그림에서 파란 박스)는 최대 힙으로 구현된 우선순위 큐이다.


역시...