📖 Conventional Circle Generating
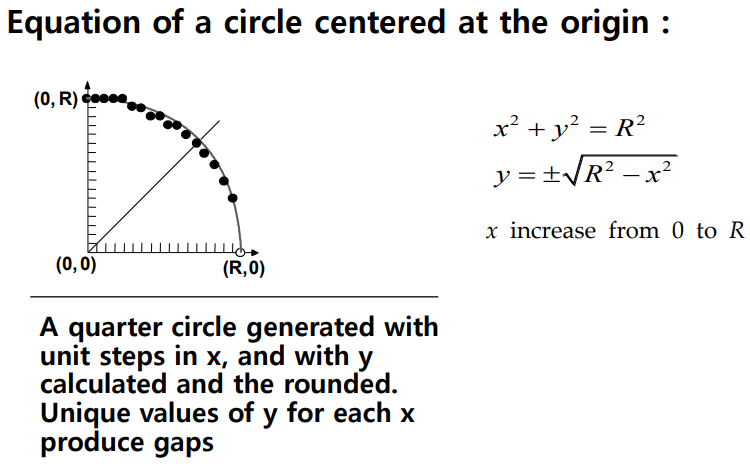
- x=0~R까지 각 x에 대해 y 값을 구하면 그것이 원점에서 R 만큼 떨어진 점들이다
- 4분원에 따라 x와 y의 값을 바꾸면서 구할 수 있다(좌표계에서 1,2,3,4분면으로 나뉘어 있으므로)
- 각 x에 따라 y의 값의 차이가 크다(일정하지 않음)
 8분원으로 나눴을 경우 문제점
8분원으로 나눴을 경우 문제점
-
x에 따라 픽셀들의 밀도 차이가 생긴다 (간격이 일정하지 않음)
- 두번째 Octant는 밀도가 좋지만, 첫번째 Octant는 밀도가 좋지 않다
- 화질(해상도)에 영향을 끼침
- 기울기에 따라 생기는 문제
-
시간이 많이 걸린다
- sqrt, *, round, 실수 산수
📖 Polar(Non-Cartesian) Coordinate System
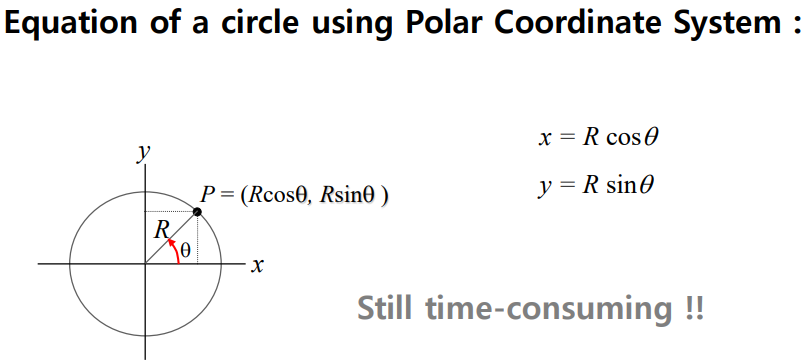
- 각도를 변수로 사용하면 간격이 일정하지 않는 문제점 해결

- 삼각함수를 계산해야 하므로 시간은 여전히 많이 걸린다.
📖 Eight-Way Symmetry (8방향 대칭성)
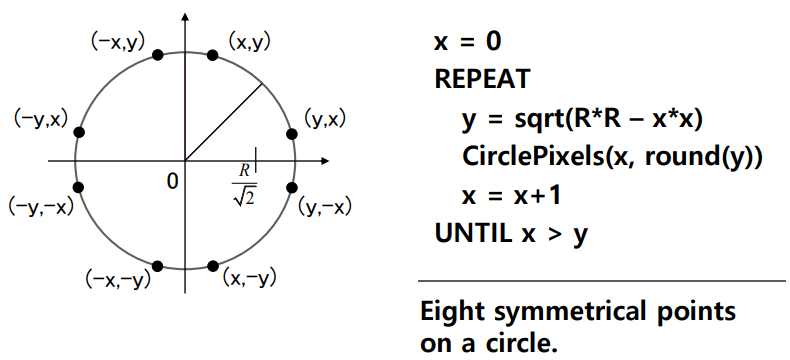
-
두번째 Octant가 밀도 높은 점을 이용해서 두번째 Octant만 구하고 8방향에 맞춰 x,y값 변경
-
구간을 줄여서 계산식 시간효율도 챙기고, 픽셀 간격도 줄일수 있다
-
두번째 Octant는 ~ 에 대한 y값 모음이다
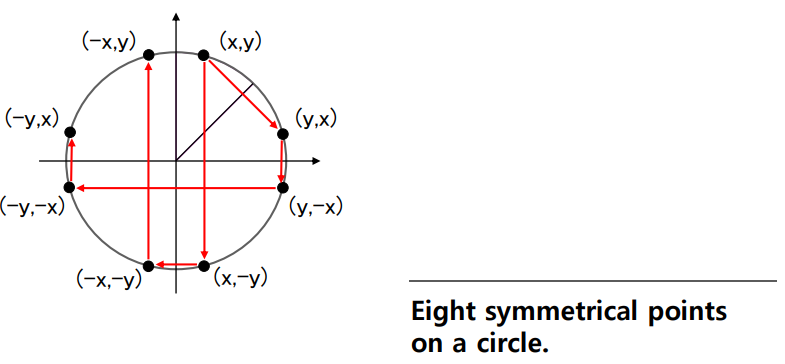
- 2 Octant를 구해, 나머지 7부분은 위 그림처럼 값 바꿔주면 된다
📌 Midpoint Circle Algorithm
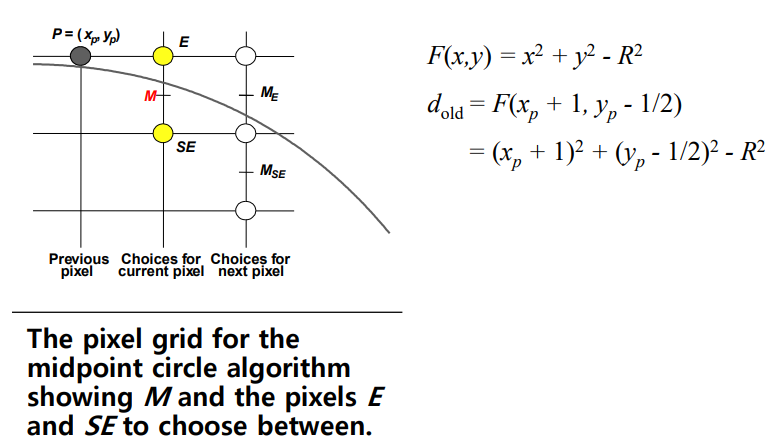
-
Midpoint Line Algorithm과 완전 동일하다. 원 방정식만 넣으면 됨
-
맨 처음 값은 시작점 으로 계산한다.
-
첫 값 기준, 이고, 이는 이다
-
이 말은, 첫 값 기준 값은 라는 뜻이다. (, 는 원 위에 있는 점이므로)
기준 값은 이고, 이 값을 라고 칭하면,
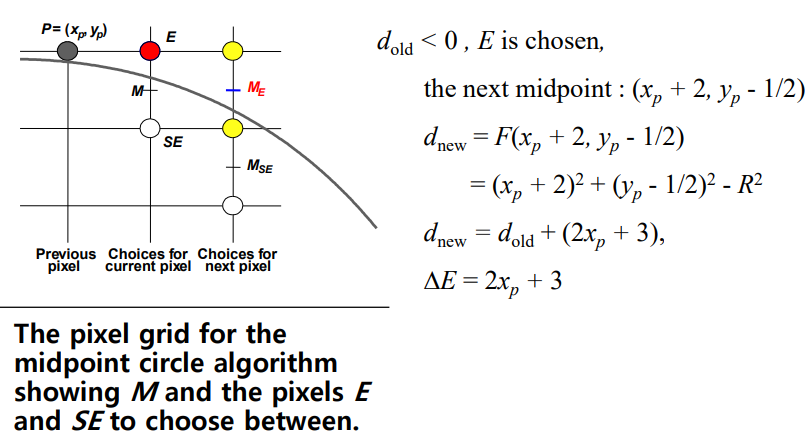
-
가 선택되었을 경우, 다음 에 대한 d값은 이다
-
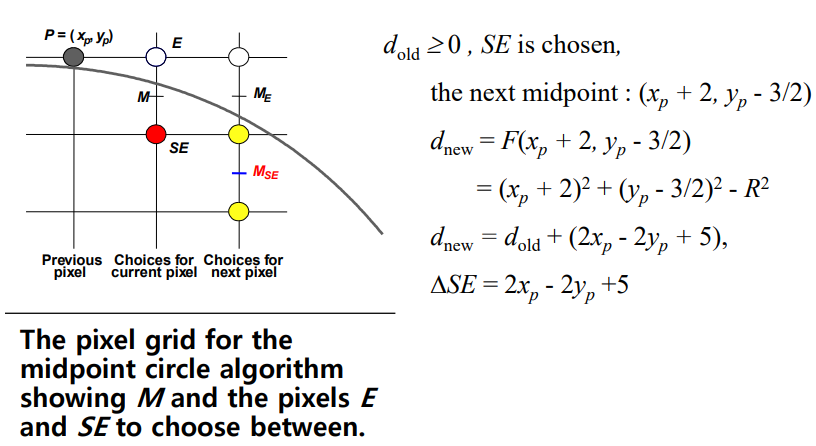
- SE가 선택되었을 경우, 다음 M에 대한 d값은 이다
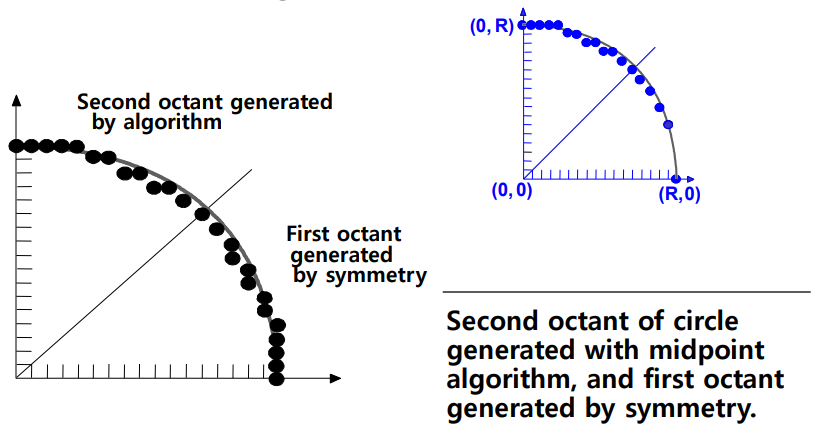
- 최종 알고리즘에 따라 나온 Second Octant를, 다른 Octant에 맞게 값만 바꿔 처리하면 된다
void MidpointCircle(int x0, int y0, int radius, int value) {
int incrE, incrNE, d, x, y, r;
r=radius;
x =0; //(x0,y0)는 원점
y =r-1; //(x, y)는 Eight way를 표현하기 위해 사용하는 값
d =2x0-y0+5/4; //맨 처음 M값에 대한 d값
incrE=2x0+3; //E가 채택되고 다음 M값에 대한 d값 증가량
incrSE=2x0-2y0+5; //SE가 채택되고 다음 M값에 대한 d값 증가량
SetCirclePoints(x0,y0,x,y,value);
while(x<y) {
if (d <= 0) {
d += incrE;
x++;
}
else {
d += incrSE;
x++;
y--;
}
SetCirclePoints(x0,y0,x,y,value);
}
}
void SetCirclePoints(int x0, int y0,int x,int y,int value){
WritePixel(x0 + x, y0 + y, value);
WritePixel(x0 + y, y0 + x, value);
WritePixel(x0 + y, y0 - x, value);
WritePixel(x0 + x, y0 - y, value);
WritePixel(x0 - x, y0 - y, value);
WritePixel(x0 - y, y0 - x, value);
WritePixel(x0 - y, y0 + x, value);
WritePixel(x0 - x, y0 + y, value);
}
[출처] Scan Converting Circles|작성자 노트📖 Summary
- 원(circle)은 선분의 경우와 달리 2차 방정식으로 표현되어 계산 시간이 더 걸린다.
- 따라서 계산 시간의 절약을 위해서 원이 가지는 8-방향 대칭성을 이용한다
- 정수형 연산만으로 이루어진 스캔 변환 알고리즘을 구현하는 것이 중요하다.
