[CGs] Parametric (Bi)Cubic Curves(Surfaces)

매개변수형 3차곡선(곡면)

• cubic = 4개의 점으로 3차 다항식
• 3차 다항식으로 정의되는 곡선
• n개의 점 : n-1차 다항식

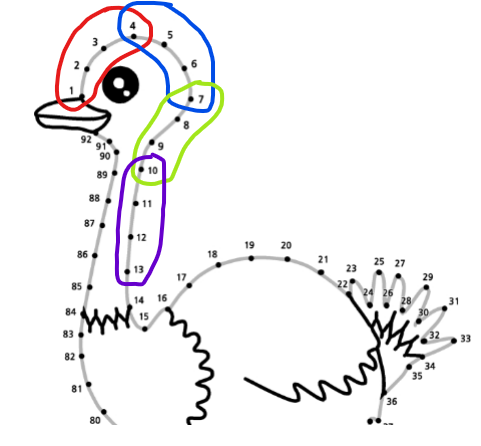
위 그림은 총92개의 점으로 91차 다항식이지만 이는 현실적으로 불가능하다.
따라서 연속된 3차 다항식으로 위의 그림을 표현한다.

• Joint point : 연결포인트 (연속성을 가짐)
  • ex) 4, 7, 10, 13 ...

Displaying 3D Curved Lines and Surfaces

• 객체를 정의하는데 다항식 사용

  • 고차 다항식이 필요

• 사용자 지정 데이터 포인트 집합 사용

  • 사용자가 제공하는 점을 가지고 곡선을 표현(3차 다항식을 이어서 곡선을 표현)

  • 객체의 모양(외곽)을 본 뜬 점들을 만든다.

  • Spline 곡선을 사용하여 부드러운 곡선과 곡면 표현

  • 이러한 방법은 일반적으로 새로운 객체 모양을 설계하고 도면을 디지털화하며 애니메이션 경로를 설명하는데 사용된다.

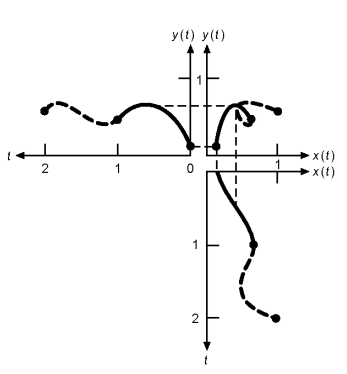
Basic Characteristics(기본 특성)

• 곡선을 정의하는 매개변수형 3차 다항식

• 곡선의 조각들을 이어 하나의 큰 그림 만들기

  • 각 곡선은 3차로 정의

  • 이어지는 부분은 부드럽게

Interpolation Splines(보간 곡선)

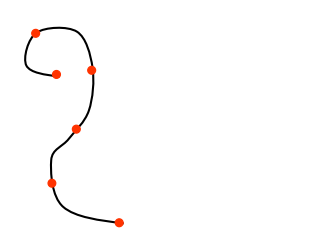
• 제시된 점들을 시작부터 마지막까지 모두 통과하는 곡선

Approximation Splines(근사 곡선)

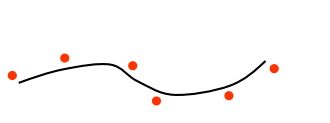
• 주어진 점들의 근처를 지나가는 곡선
• 점들의 역할 : 곡선이 지나가는 경로에 대해 인력을 부과

Convex Hull

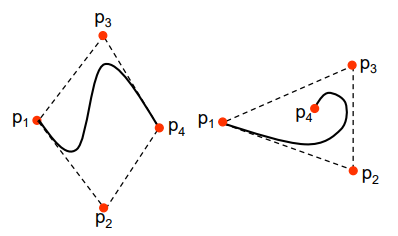
• 점들로 둘러진 볼록다각형의 경계선
• 곡선을 완전히 포함하는 다각형, 만들어지는 곡선의 모양을 예측할 수 있는 근거가 된다.
• Control point 두개 통과($P_{1}$,$P_{4}$) - 첫점과 끝점은 보간
• 이외의 point는 근사 곡선으로 선을 땡겨주는 역할

---

Continuity between Curve Segments

• 곡선 조각을 이어서 전체의 완전한 조각을 만든다. 이 때 각각의 곡선 조각들은 3차 다항식

• 연속 조건 2가지

  • Parametric Continuity Condition
  • Geometric Continuity Condition

• 필요에 따라 연속 조건을 접점에 부여

Parametric Continuity Condition

• $C^{0}$ : 0차 Parametric Continuity

  • 단순히 2개의 곡선 조각이 연결점에서 만나기만 하면 0차의 연속 조건 만족

• $C^{1}$ : 1차 Parametric Continuity

  • 연결점에서 각각 tangent line(접선)의 기울기가 같도록 2개의 곡선 조각이 이어져야 한다.

  • 즉, 접선의 기울기만 같으면 된다.

  • 보통 1차 연속 조건만 부여해도 일반적인 객체의 현상을 부드럽게 만드는데 지장이 없다.

• $C^{2}$ : 2차 Parametric Continuity

  • 연결점에서의 1차 미분(접선의 기울기)뿐만 아니라 2차 미분(기울기의 변화율)까지 같아야 한다.

  • 접선의 기울기와 변화율까지 같다는 의미는 이어지는 연결점에서 부드럽게 이어지는 것 뿐만아니라 이후에 급격하게 곡선의 모양이 바뀌는 것을 방지한다.

  • ex) Animation Path, 정밀 CAD, Camera Path

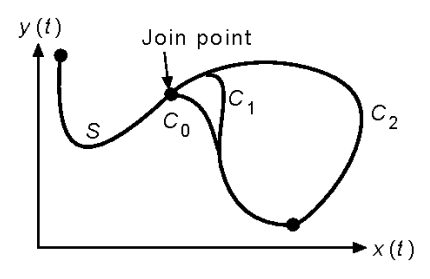
• $C^{2}$는 기울기가 $C^{1}$처럼 급작스럽게 변하지 않음.

Geometric Continuity Condition

• $G^{0}$ : 0차 Geometric Continuity

  • 단순히 곡선 조각들이 서로 이어지는 접점에서 좌표값만 같으면 된다.

• $G^{1}$ : 1차 Geometric Continuity

  • tangent vector의 방향만 같으면 된다. (크기는 달라도 상관 없음)

  • 따라서 $C^{1}$이 $G^{1}$ 보다 더 엄격한 1차 연속 조건이다.

  • $C^{1}$ 조건을 만족한다면 $G^{1}$ 조건을 만족

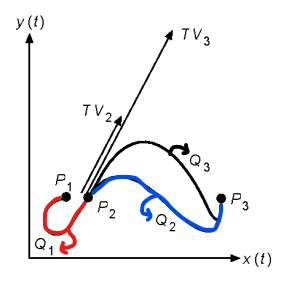
• $G^{2}$ : 2차 Geometric Continuity

  • 연결 접점에서 tangent vector의 방향은 같고 크기의 변화율이 서로 비례해서 변한
    다.
  • $C^{2}$처럼 접점의 기울기 변화율이 같은 것이 아니라 비례해서 커지거나 작아질 수 있다.

• $TV_{2}$와 $TV_{3}$의 방향은 같지만 크기는 다르다.

• $Q_{1}$ , $Q_{2}$ : $C_{1}$ 조건을 만족하면서 연결된 것

• $Q_{1}$ , $Q_{3}$ : $G_{1}$ 조건을 만족하면서 연결된 것