[CGs] Three Major Types of Curves

• 각각의 곡선 조각 $Q(t)$ 는 매개변수형 3차 다항식으로 정의

  • 끝점, tangent vector, 연속 조건 존재

  • 이들을 이용하여 4개의 식을 만들어내고 제약조건을 어떻게 만들어 내느냐에 따라 여러 형태의 곡선이 정의된다.

• 3차 다항식 : $ax^{3}+bx^{2}+cx+d$

  • 4개의 계수가 존재 (4개의 미지수를 풀기 위해 4개의 식 필요)

  • 4개의 제약 조건을 사영해서 4개의 식을 만들어내고 이 4개의 식으로부터 4개의 계수를 결정

Hermite curve

• 두개의 끝점(endpoints)과 두 끝점에서의 tangent vector를 이용해서 4개의 제약조건 만든다.

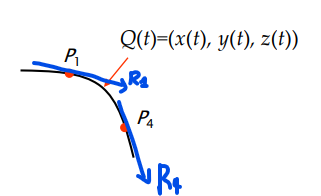
• 끝점 $P_{1}$ 및 $P_{4}$의 제약 조건과 끝점에서의 tangent vector $R_{1}$ 및 $R_{4}$에 의해 결정된다.

Family of Hermite Parametric Cubic Curves

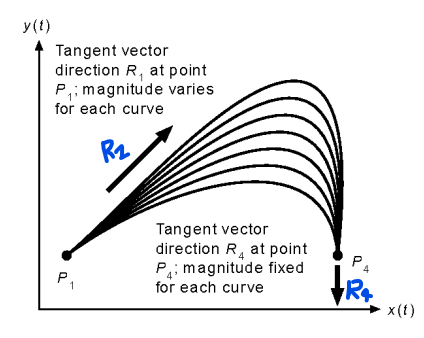
• $R_{4}$는 모두 동일한 곡선 7개

• $R_{1}$의 크기에 따라 만들어지는 여러개의 곡선

• $R_{4}$는 모두 동일

• $R_{1}$의 크기는 같고 방향만 다른 곡선

Interactive Control of the Hermite Curves

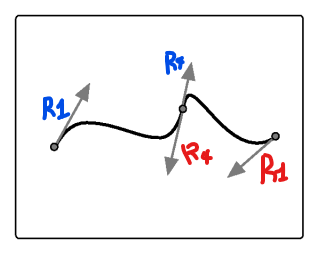
2개의 곡선이 연결되어 있는 상태이다.
그림 상에서 $R_{4}$ 와 $R_{4}$ 는 방향과 크기가 다르므로 접점은 $C^{0}$의 조건을 만족한다.

---

Bezier Curves

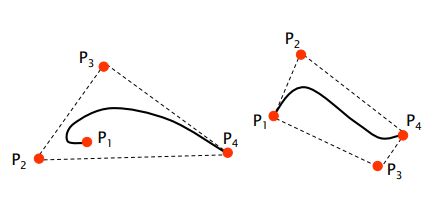
• 두개의 끝점과 두개의 중간점 사용
• 두 끝점은 interpolation(보간) 제약 조건 사용 - 2개
• 두 중간점은 Approximation(근사) 제약 조건 사용 - 2개

Joining of Bezier Curve Segments

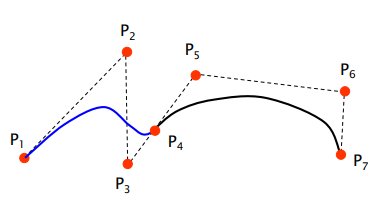
• $P_{3} - P_{4}$ = $k(P_{4}-P_{5})$라면 두 vector는 일직선. 즉, $G^{1}$조건 만족

• $k$ = 1일 경우 $C^{1}$ 조건 만족

  • 즉, $P_{3} - P_{4}$ = $P_{4}-P_{5}$이므로 두 vector의 크기는 같다.

• $k$ != 1일 경우 $G^{1}$

Bezier Surfaces

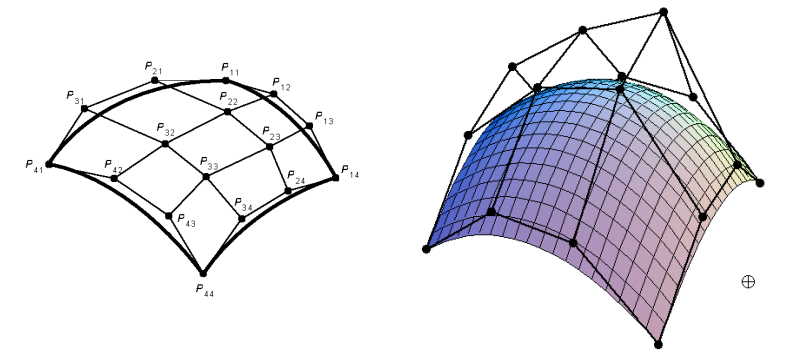
• Bezier Surfaces에 대한 매개변수 벡터 함수는 Bezier 혼합 함수의 데카르트 곱으로 형성된다.

Joining of Two Bezier Patches

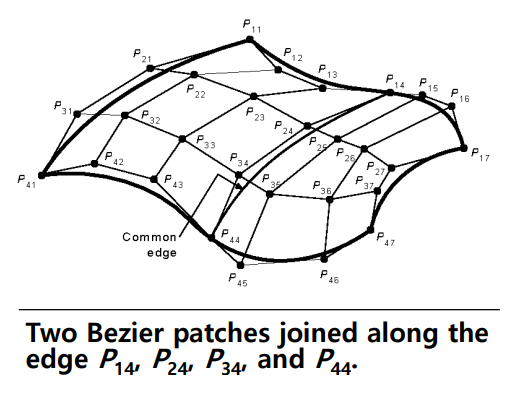
Several kinds of Splines

• 다양한 형태의 Spline이 존재하는데 제약조건을 어떻게 부여하느냐에 따라 결정
• 4개의 control points 사용

Summary

• 곡선과 곡면의 표현법

  • 곡선과 곡면 모델링은 사실감 있는 물체 표현을 위해 필수적인 기법

  • 폴리곤 매쉬에 의한 곡면 표현 모델링 기법

  • 매개변수형(Hermite, Bezier) 3차 곡선 및 곡면 표현 모델링 기법