[CGs] Filling Polygons

박원준·2023년 3월 24일

컴퓨터 그래픽스

CGs

목록 보기

6/20

💻 General Ideas about Polygon Filling

3 Types of Polygons

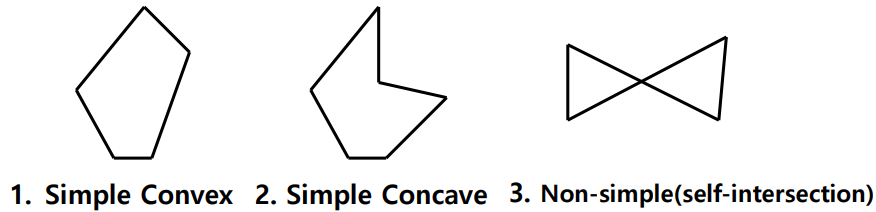
Simple Convex(볼록)
Simple Concave(오목)
Non-simple Polygon(Self-intersection : 교차)

Some Problems

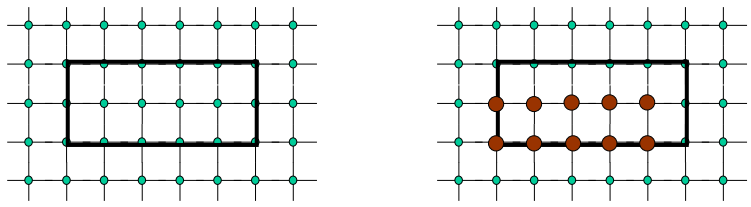
다각형의 경계선에서 위쪽과 오른쪽의 경계선은 왜 채우지 않을까?
✍️ Double-filling Problem : 두 개의 polygon이 인접하게 되면 두번 그려지는 현상

비효율적
마지막 색상은 polygon이 그려진 순서에 따라 결정되고, flicker현상이 나타날 수도 있다.
착시현상 발생할 수도 있다.

따라서, 위쪽과 오른쪽을 채우지 않음으로써 서로 인접하게 돼도 Double-filling problem이 나타나지 않도록 한다

General Ideas about Polygon Filling

✍️ Rules for shared edges

사각형의 오른쪽 edge는 채우지 않는다
사각형의 위쪽 edge는 채우지 않는다

💻 Illustration of Filling Polygon

컴퓨터는 내부, 외부를 scan line 단위로 판별한다.
하나의 scan line을 가지고 한 쌍의 교차점이 있다면 두 교차점 사이는 내부이다.

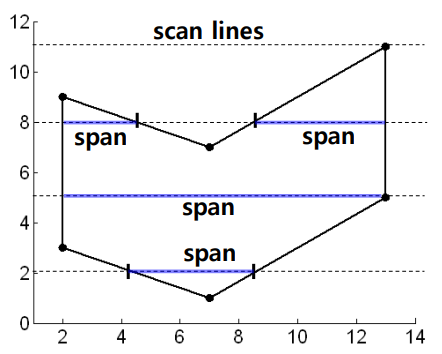
✍️ Span : 한 쌍의 교차점에 의해 내부 픽셀로 판정된 픽셀들의 모음, 내부 픽셀들
공간의 일관성 : 같은 scan line상의 이웃한 픽셀들 또는 이웃한 scan line들은 같은 속성일 가능성이 높다.
edge 일관성 : scan line i에 교차하는 많은 edge는 scan line i+1에도 교차한다.
-> (밑에서 자세히 소개)

💻 Filling The Spans

✍️ 3가지 단계 존재
1. scan line과 다각형의 변과 교차점 계산(일관성을 이용하면 편리)
2. 교차점의 x좌표를 기준으로 오름차순으로 정렬
3. 정렬 후 내부로 판정된 픽셀들을 채워준다.

✍️ 문제점

교차점을 어떻게 효율적으로 찾을 것인가?
어떻게 픽셀이 polygon 내부인지 외부인지 판단할 것인가?
- 토대 : Parity(odd-Even) Rule
- 기준은 총 4가지로 구성

Parity (Odd - Even) Rule

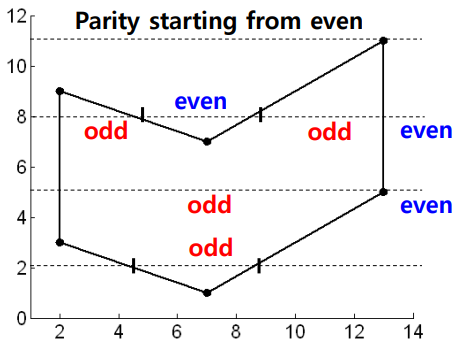
✍️ Parity로 내부/외부 판정

교차점을 만날 때 마다 Parity값을 갱신
ex) 초기 Parity = 0일경우 교차점을 지나 1로 변경되면서 도형의 내부로 들어가고 다시 교차점을 지나 짝수가 되면서 도형을 빠져나가게 된다. 그럼 홀수의 값을 가진 픽셀들은 내부로 판정

4가지 Elaboration of 2nd Question

✍️ 픽셀이 내부인지 외부인지 판단하는 4가지 기준

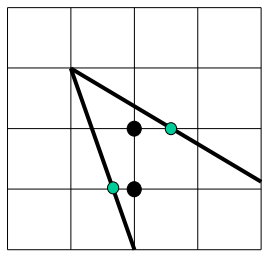
Q1 : $x$ 값의 교차점이 실수로 주어지면 어떻게 어떤 픽셀이 내부에 있다는 것을 정의하는가?
A1 : 엄격한 내부 룰로 정의

어떻게든 안쪽인 픽셀을 선택한다.
도형으로 들어가는 교차점의 경우 다음 픽셀부터 내부, 나올때는 전 픽셀까지 내부

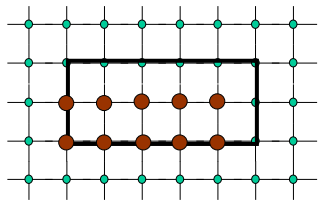
Q2 : 정수 픽셀 좌표의 교차점같은 특별한 상황에서는 어떻게 처리할 것인가?
A2 : 공유되는 픽셀 사이에 충돌을 피하는 기준을 사용한다

만약 span에서 왼쪽 끝 픽셀이 정수 $x$ 좌표를 가지면, 그것은 내부로 정의한다
만약 오른쪽 끝 픽셀이 정수 $x$ 좌표를 가지면, 그것은 외부로 정의한다

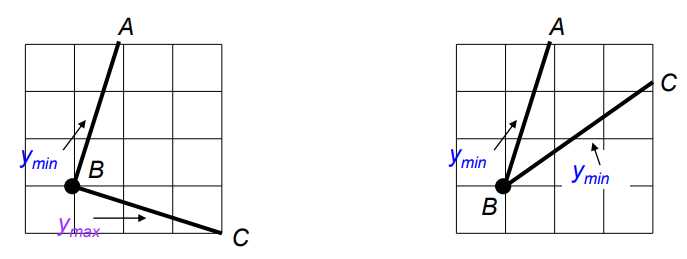
Q3 : 공유된 꼭짓점에 대해서는 어떻게 처리할 것인가?
A3 : $y_{min}$ 꼭짓점의 개수에 따라 parity를 계산해 처리한다
변과 꼭지점의 정보는 이미 알고 있다.

🖊️ ex) 첫번째 그림의 공유된 꼭짓점 : B

AB선분에선 B의 y는 A의 y보다 작으므로 $y_{min}$ → parity계산 한다
BC선분에선 B의 y는 C의 y보다 크므로 $y_{max}$ → parity계산 하지 않는다
따라서 B이후 parity는 홀수가 되어 polygon 내부로 처리한다

🖊️ ex) 두번째 그림의 공유된 꼭짓점 : B

AB선분에선 B의 y는 $y_{min}$ → parity계산 한다
BC선분에선 B의 y는 $y_{min}$ → parity계산 한다
따라서 B이후 parity는 짝수가 되어 polygon 외부로 처리한다

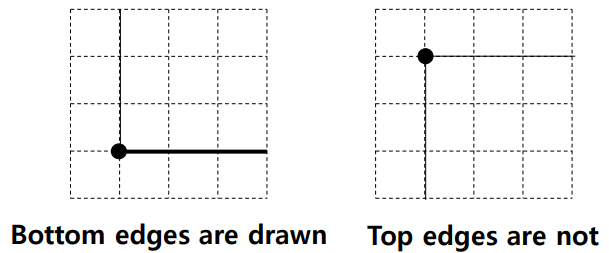
Q4 : 꼭짓점이 수평한 edge에 있는 특수한 상황은 어떻게 처리할 것인가?
A4 : bottom edge는 내부로, top edge는 외부로 처리

🖊️ ex) 첫번째 그림의 공유된 꼭짓점

수직선분에선 y는 ymin → parity계산 한다
수평선분에선 y는 ymax도 ymin도 아니다→ parity계산 하지 않는다
따라서 꼭짓점 이후 parity는 홀수가 되어 polygon 내부로 처리한다

🖊️ ex) 두번째 그림의 공유된 꼭짓점

수직선분에선 y는 ymax → parity계산 하지 않는다
수평선분에선 y는 ymax도 ymin도 아니다→ parity계산 하지 않는다
따라서 꼭짓점 이후 parity는 짝수가 되어 polygon 외부로 처리한다

Four Elaborations

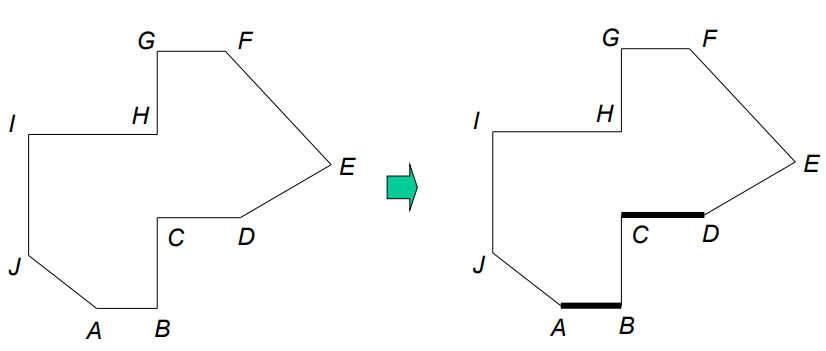
AB와 CD는 내부, IH와 GF는 외부

💻 Edge Coherence

🖊️ 매번 연립 방정식을 풀어서 교차점의 좌표값을 구하는 것이 아니라 전 단계에서 구한 좌표값을 edge간에 발생하는 일관성을 이용해서 쉽고 빠르게 계산한다.

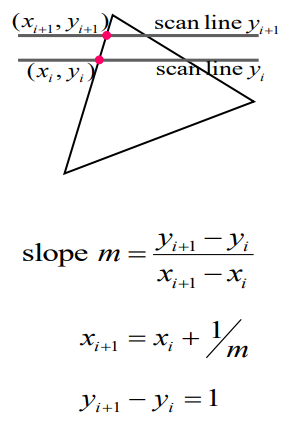
$(x_{i},y_{i})$ 와 $(x_{y+1},y_{i+1})$ 은 이웃하기 때문에 한 픽셀 차이.
$y_{i+1} = y_{i} + 1$
따라서 $x_{y+1} = x_{i} + {1\over m}$

Ex)

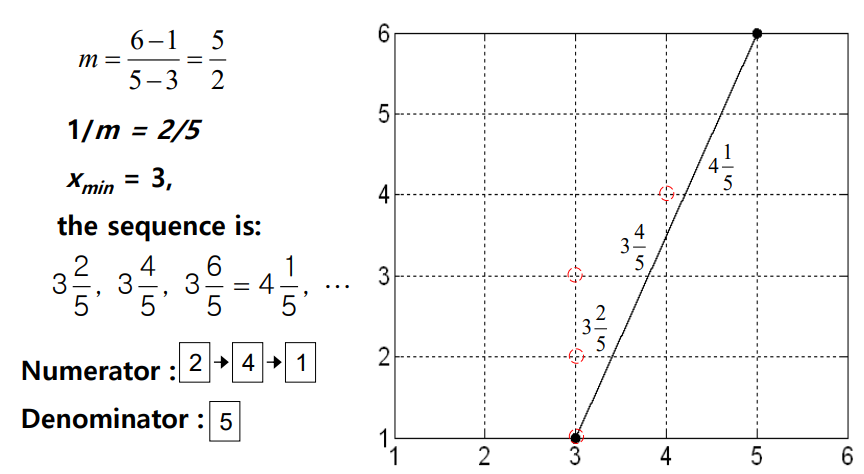
scan line i에 교차하는 많은 edge는 scan line i+1에도 교차한다
edge의 교차점 x로 새 교차점을 계산한다

Slivers

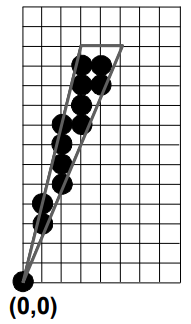
✍️ Slivers : 다각형이 가늘고 뾰족함
어떤 Scan line은 Span에 포함되는 픽셀이 없거나 아주 적을 수 있다. 이렇게 되면 시각적으로 매끄럽지 못하게 되어 퀄리티가 낮게된다.

polygon이 너무 얇아서 엄격한 내부 룰을 쓰게 되면 한 픽셀이거나 픽셀이 없는 상황이 생긴다
픽셀이 사라지는 것은 aliasing(앨리어싱) 문제의 한 예시다
🖊️ aliasing : 채워진 pixel의 개수가 아주 적거나 없어서 우리가 시각적으로 느끼는 부자연스러운 시각적 현상을 의미
anti-aliasing(안티앨리어싱) 기술이 이 문제를 해결해 준다