Introduction
DLX란?
Knuth's Algorithm X를 Dancing Links 기법을 이용해 구현한 것
Knuth's Algorithm X란?
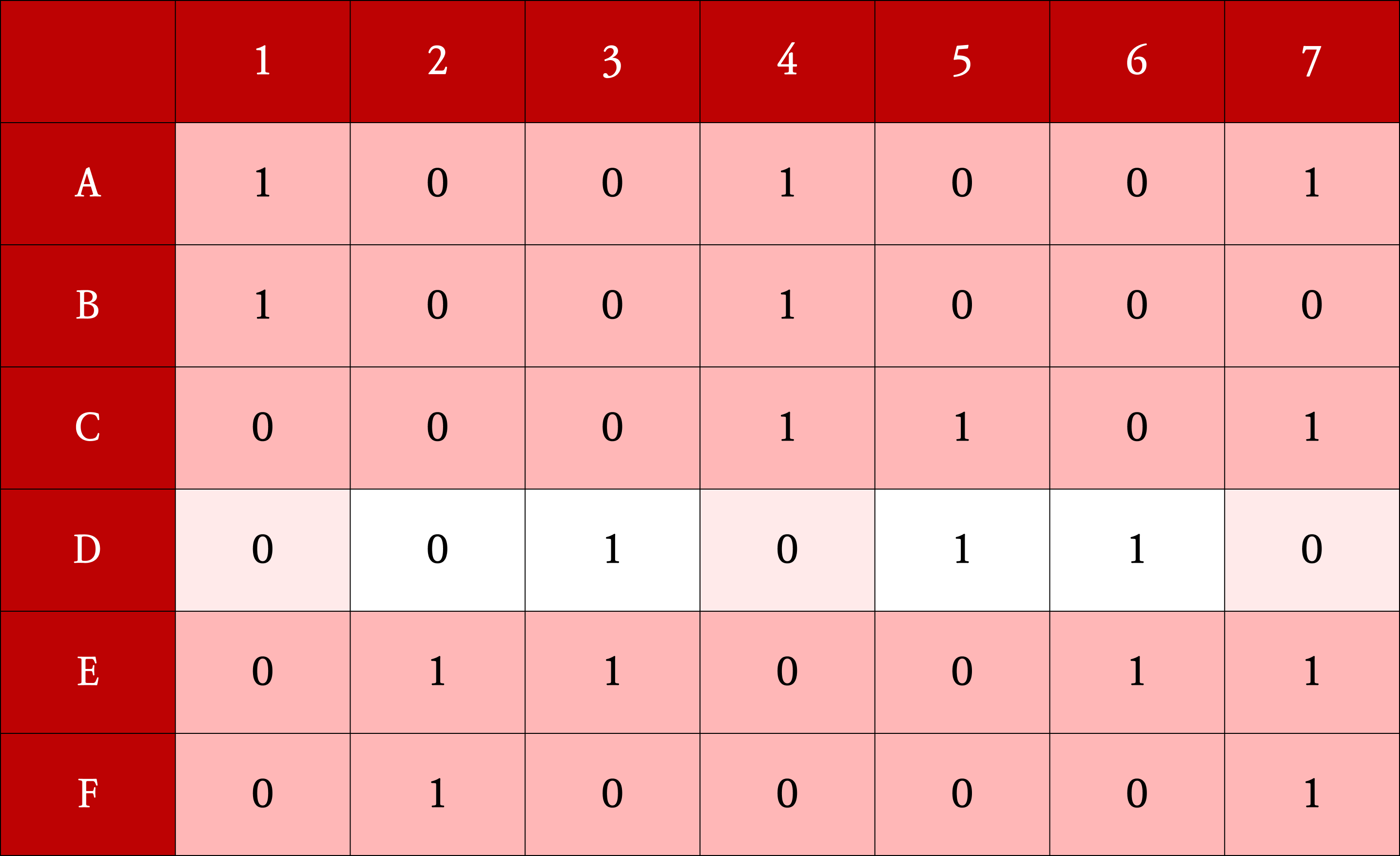
- Exact cover 문제를 0, 1로 구성된 행렬을 이용해 해결하는 방법
- Exact cover 문제는 1이 각 열에 정확히 한번씩만 등장하는 행들의 부분집합을 구하는 문제 (B, D, F)
- 여기에서 단순 백트래킹보다 속도가 더 빠른 휴리스틱 백트래킹이 Knuth's Algorithm X이다.
Knuth's Algorithm X
- 만약 행렬이 비어있지 않다면, 알고리즘을 계속 진행한다.
- 1의 개수가 가장 적은 열을 하나 선택한다. 만약, 1이 하나도 없는 열이 존재한다면 알고리즘이 실패했음을 의미하므로 해당 분기를 종료한다.
- 2에서 선택한 열에서 1이 있는 행을 partial solution에 포함 후 제거한다. (nondeterministically)
- 3에서 선택한 행에서 1이 속한 열을 모두 제거한다.
- 4에서 선택한 열에서 1이 속한 행을 모두 제거한다.
- 남은 행렬에 대해서 앞선 과정을 반복한다.
1의 개수가 가장 적은 열을 하나 선택한다.
만약, 1이 하나도 없는 열이 존재한다면 알고리즘이 실패했음을 의미하므로 해당 분기를 종료한다.

2에서 선택한 열에서 1이 있는 행을 partial solution에 포함 후 제거한다. (nondeterministically)
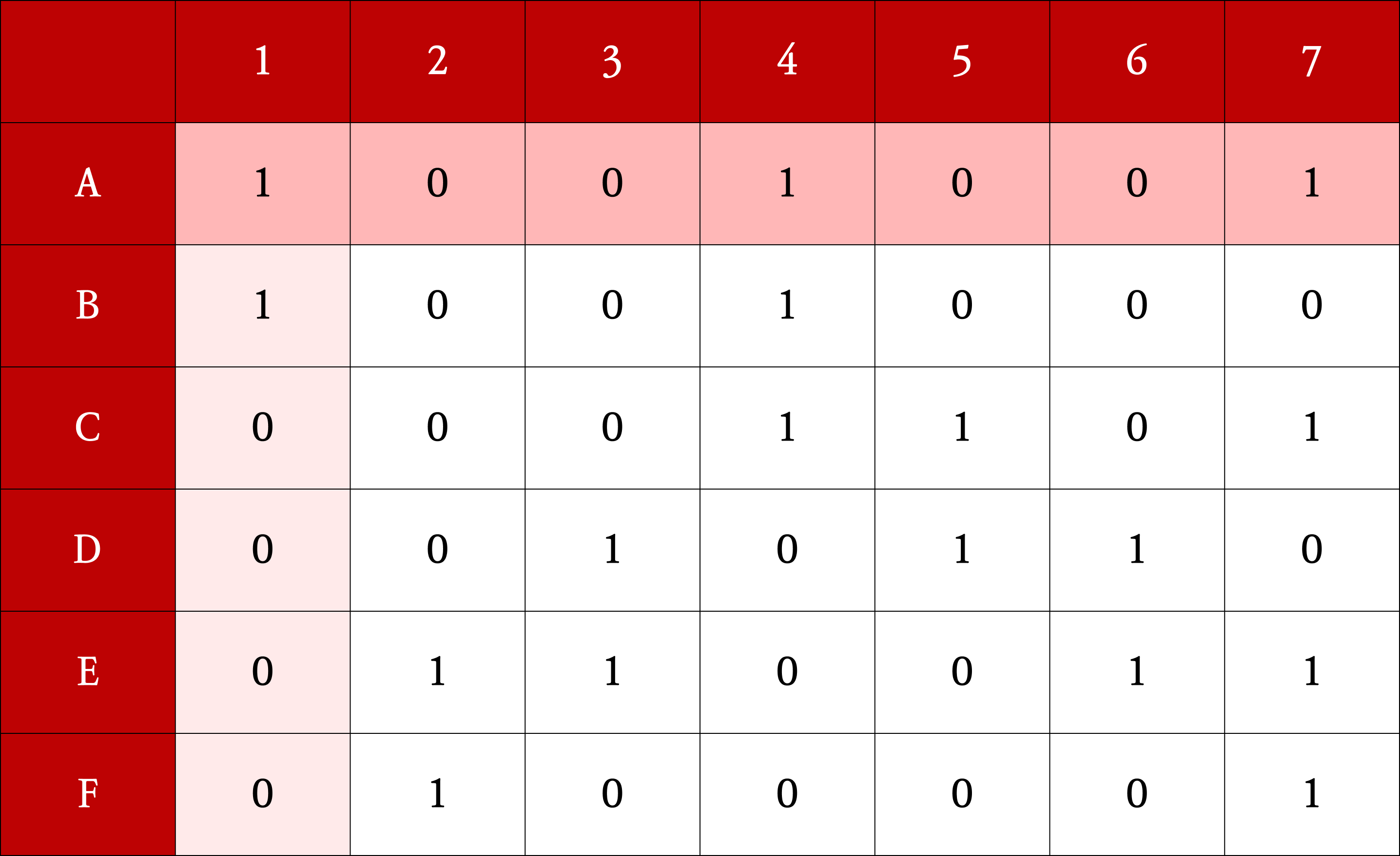
3에서 선택한 행에서 1이 속한 열을 모두 제거한다.

4에서 선택한 열에서 1이 속한 행을 모두 제거한다.
남은 행렬에 대해서 앞선 과정을 반복한다.

1의 개수가 가장 적은 열을 하나 선택한다.
만약, 1이 하나도 없는 열이 존재한다면 알고리즘이 실패했음을 의미하므로 해당 분기를 종료한다.
2에서 선택한 열에서 1이 있는 행을 partial solution에 포함 후 제거한다. (nondeterministically)
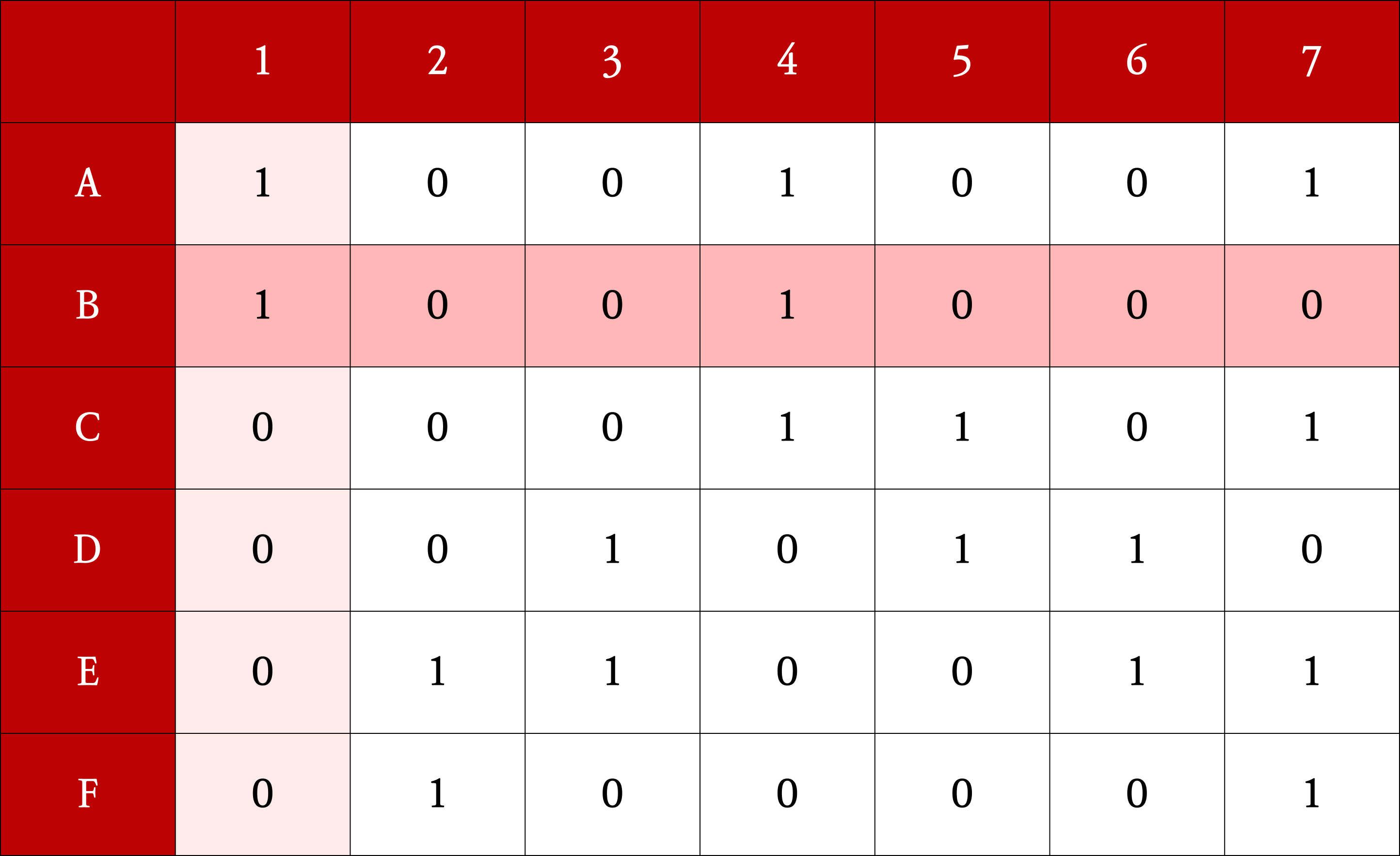
3에서 선택한 행에서 1이 속한 열을 모두 제거한다.

4에서 선택한 열에서 1이 속한 행을 모두 제거한다.
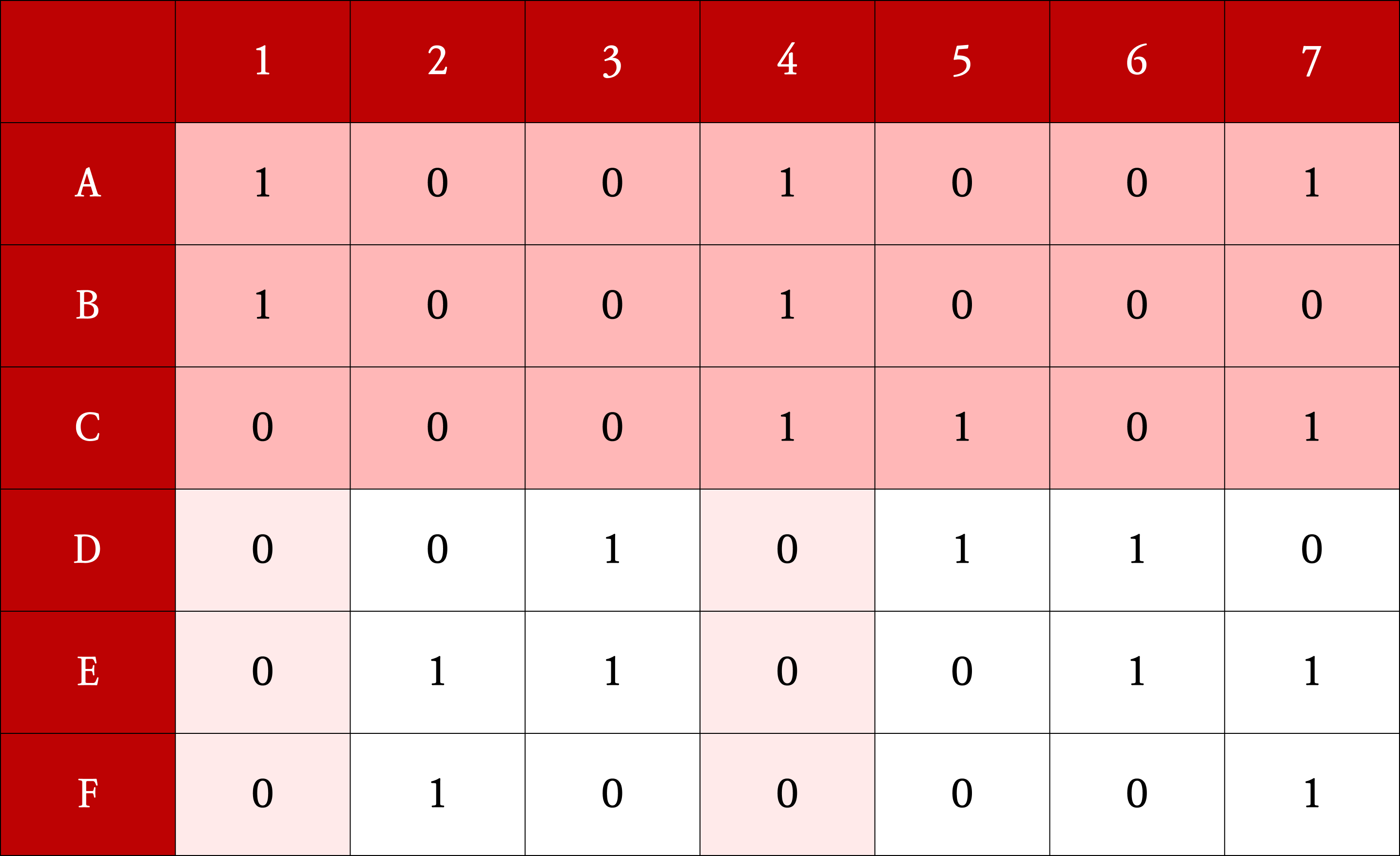
남은 행렬에 대해서 앞선 과정을 반복한다.
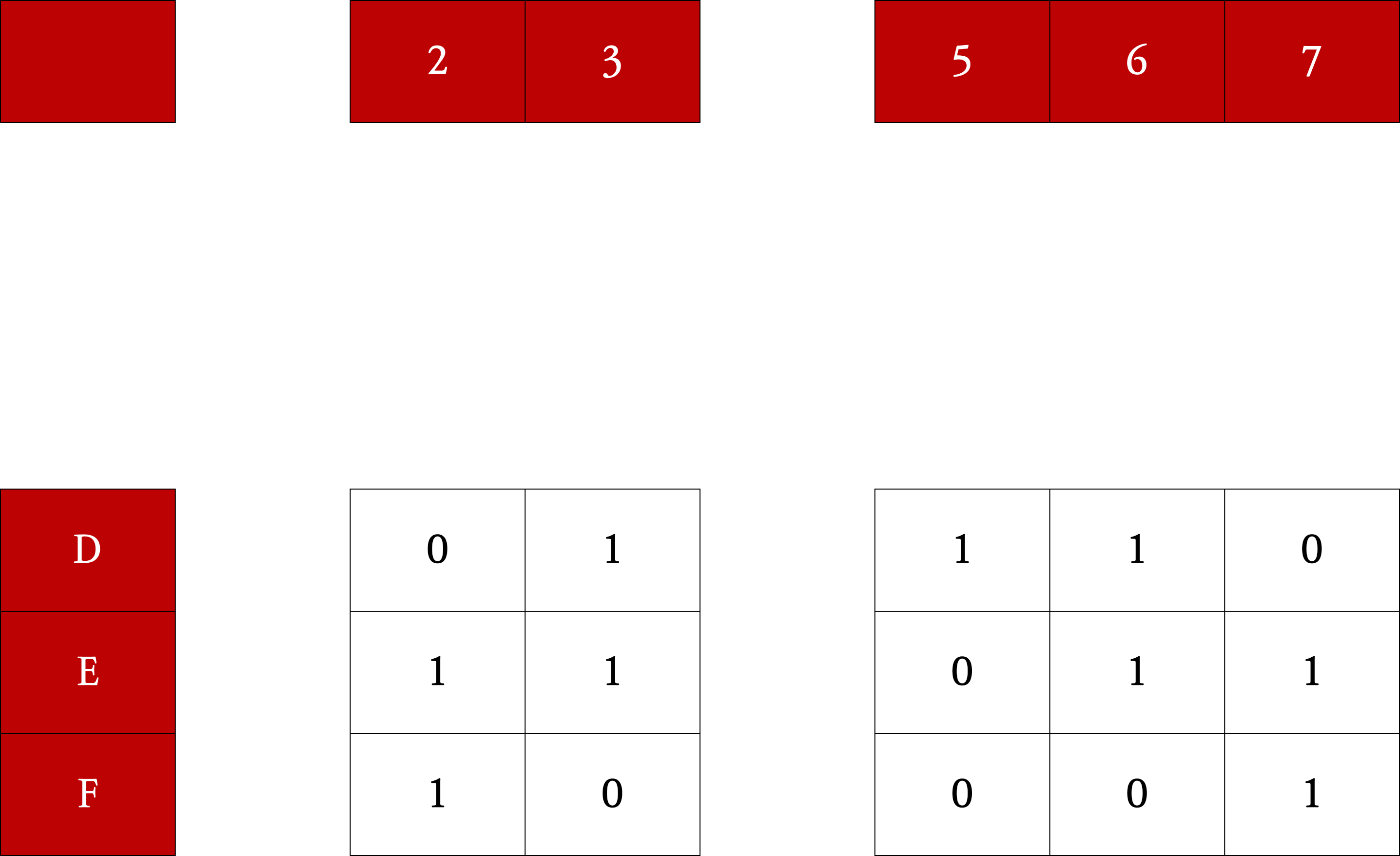
1의 개수가 가장 적은 열을 하나 선택한다.
만약, 1이 하나도 없는 열이 존재한다면 알고리즘이 실패했음을 의미하므로 해당 분기를 종료한다.
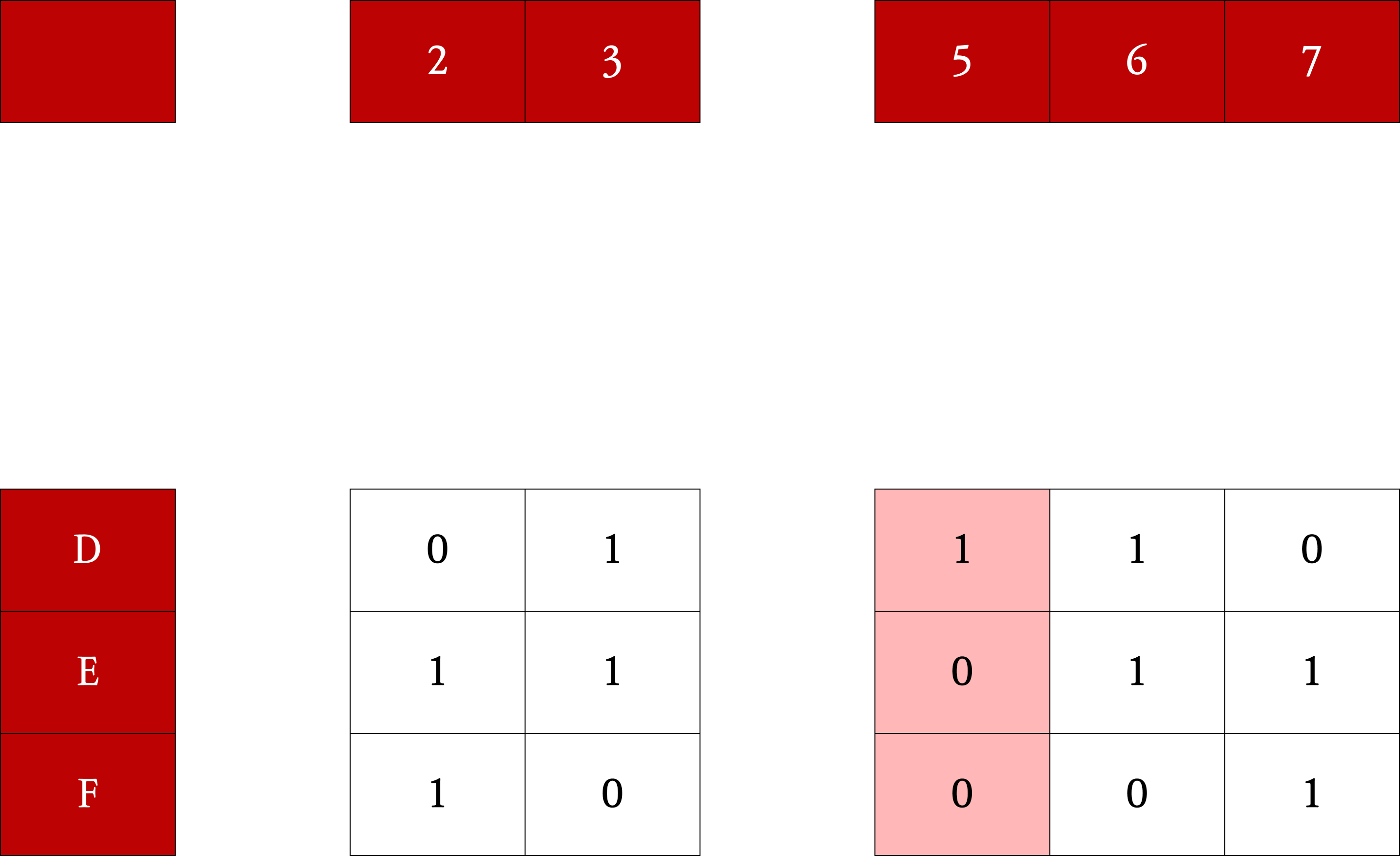
2에서 선택한 열에서 1이 있는 행을 partial solution에 포함 후 제거한다. (nondeterministically)
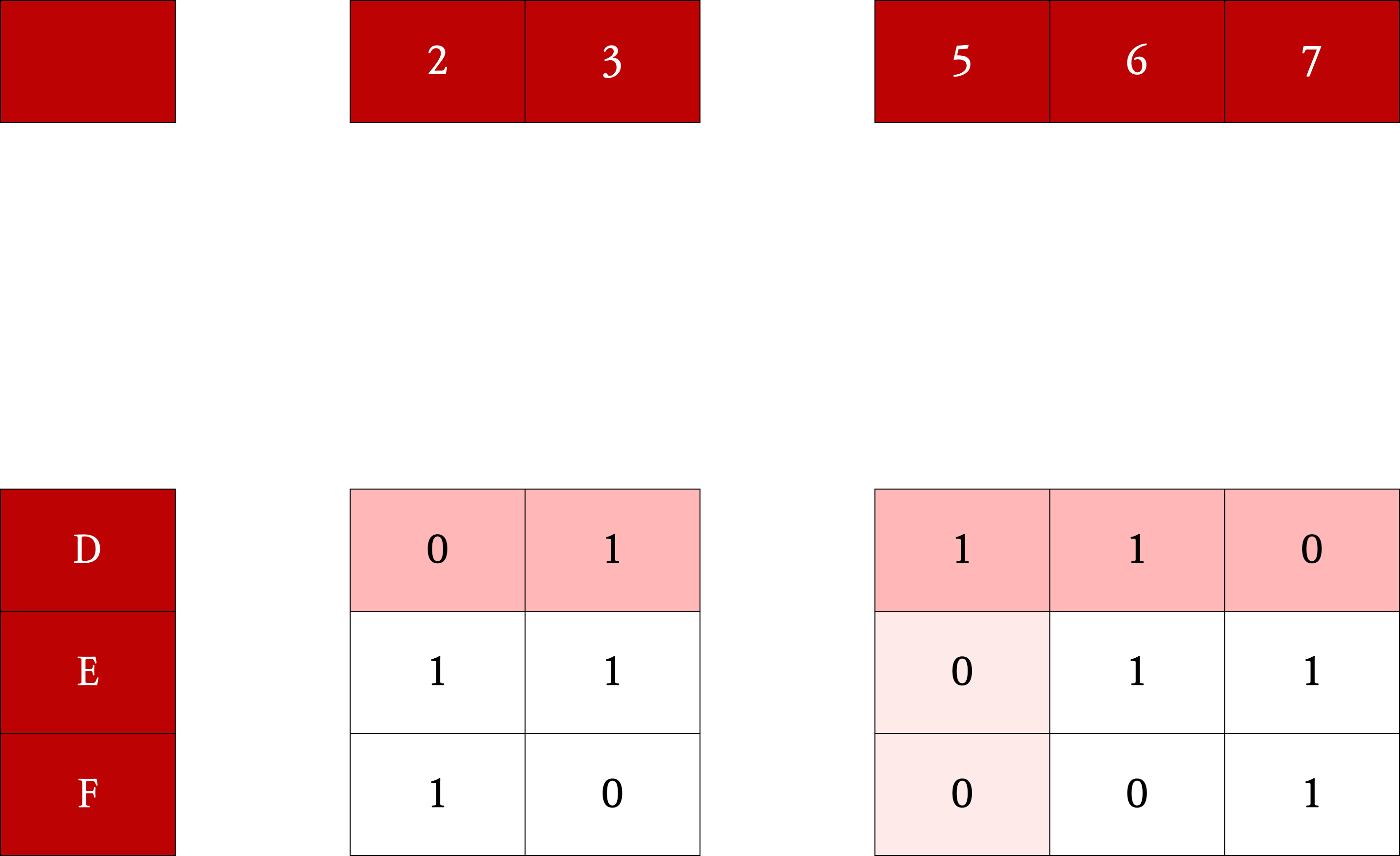
3에서 선택한 행에서 1이 속한 열을 모두 제거한다.
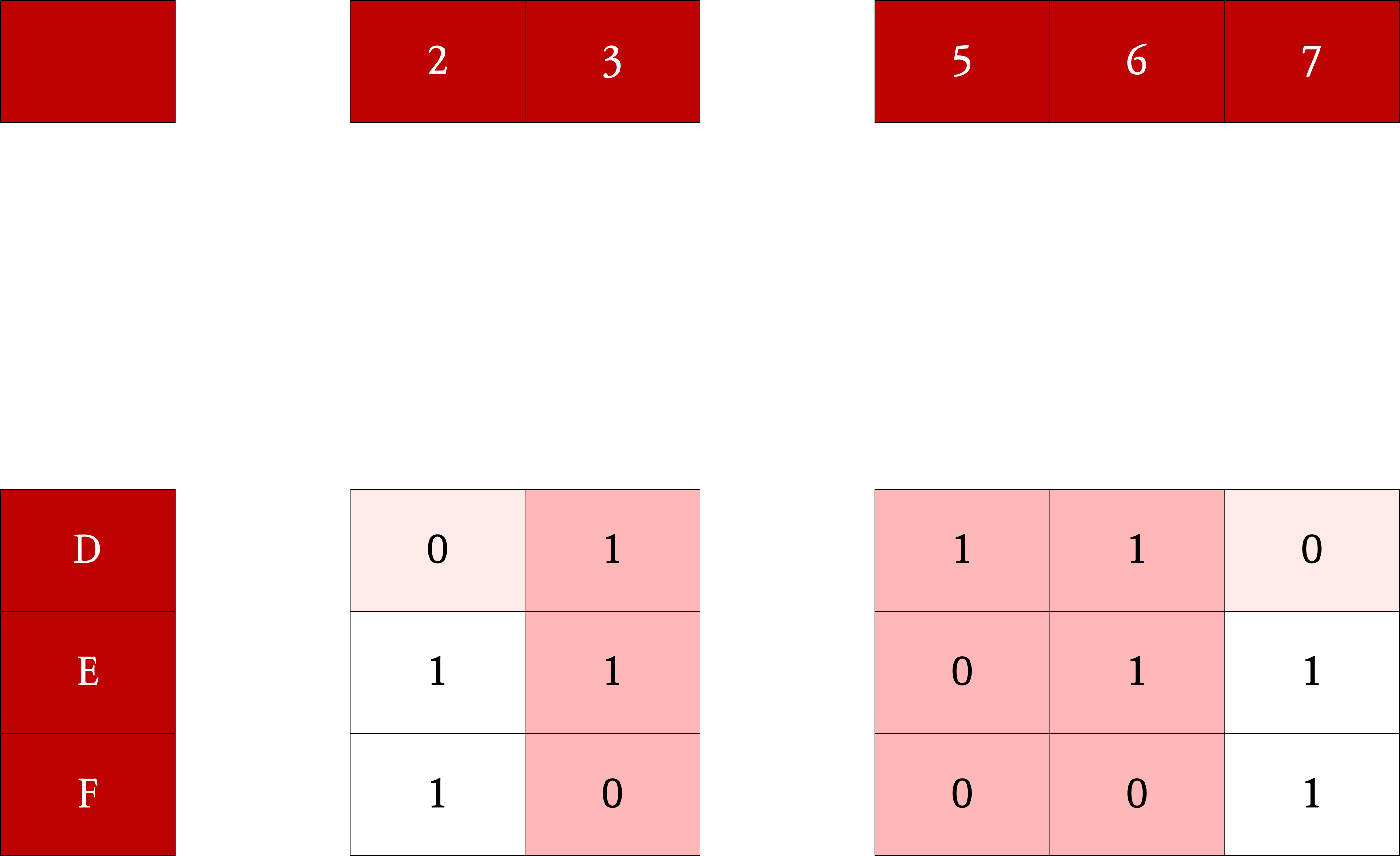
4에서 선택한 열에서 1이 속한 행을 모두 제거한다.
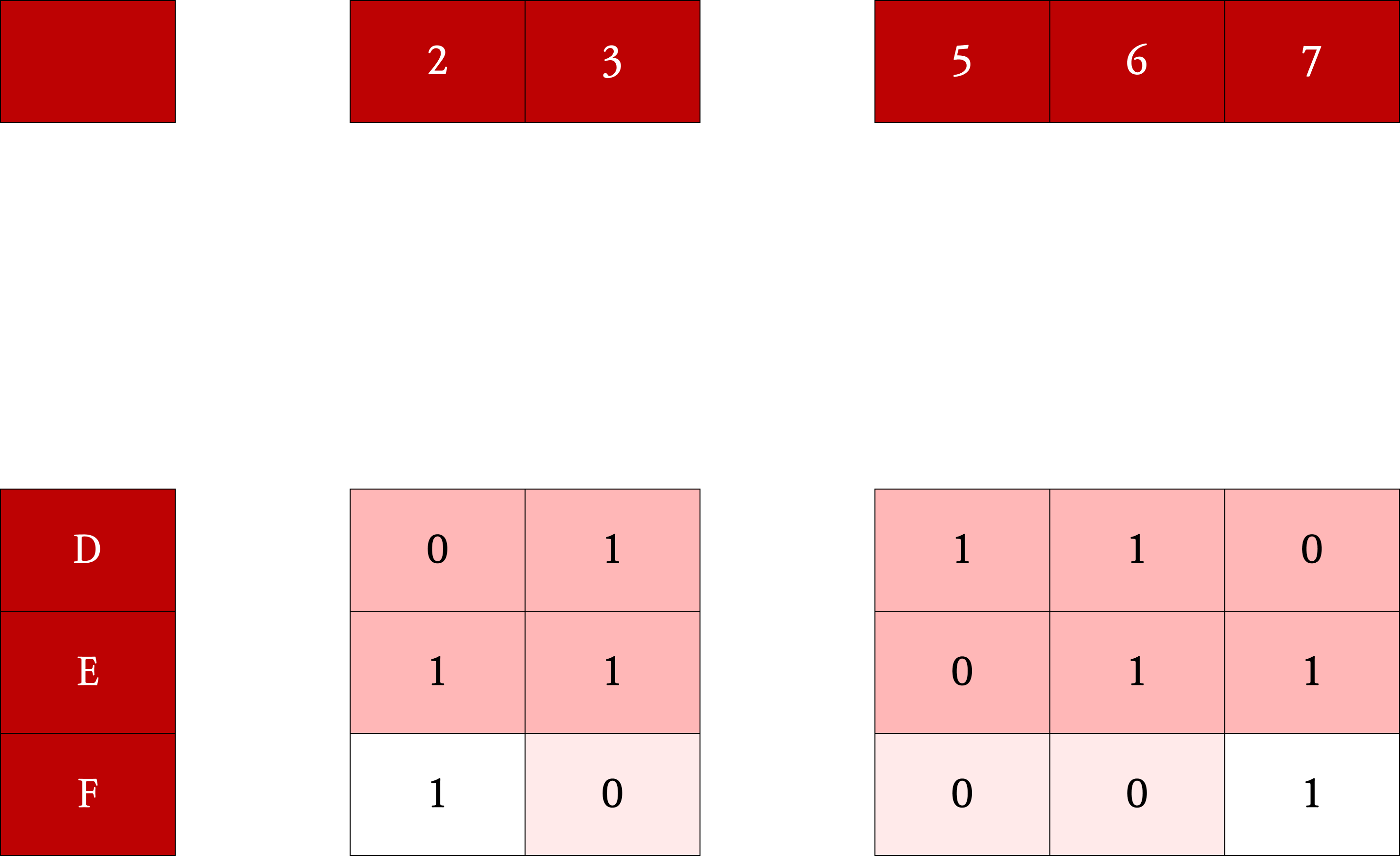
남은 행렬에 대해서 앞선 과정을 반복한다.

Knuth's Algorithm X - Applications
Sudoku

- 각 칸에는 하나의 숫자가 들어갈 수 있다. (81개 열)
- 각 열에는 1~9의 숫자가 한 번씩만 등장해야 한다. (81개 열)
- 각 행에는 1~9의 숫자가 한 번씩만 등장해야 한다. (81개 열)
- 각 3x3 칸에는 1~9의 숫자가 한 번씩만 등장해야 한다. (81개 열)
총 324개의 열이 필요하다.
행은 의 형태로 총 729개의 행이 팔요하다.

- 이제 여기에 Knuth's Algorithm X를 적용하면 스도쿠 문제를 해결할 수 있다.
Dancing Links
원형 이중 연결 리스트 (Circular Doubly Linked List) 에서 노드 삽입 및 제거를 편리하게 할 수 있도록 하는 기법

x.left.right = x.right;
x.right.left = x.left;
DLX
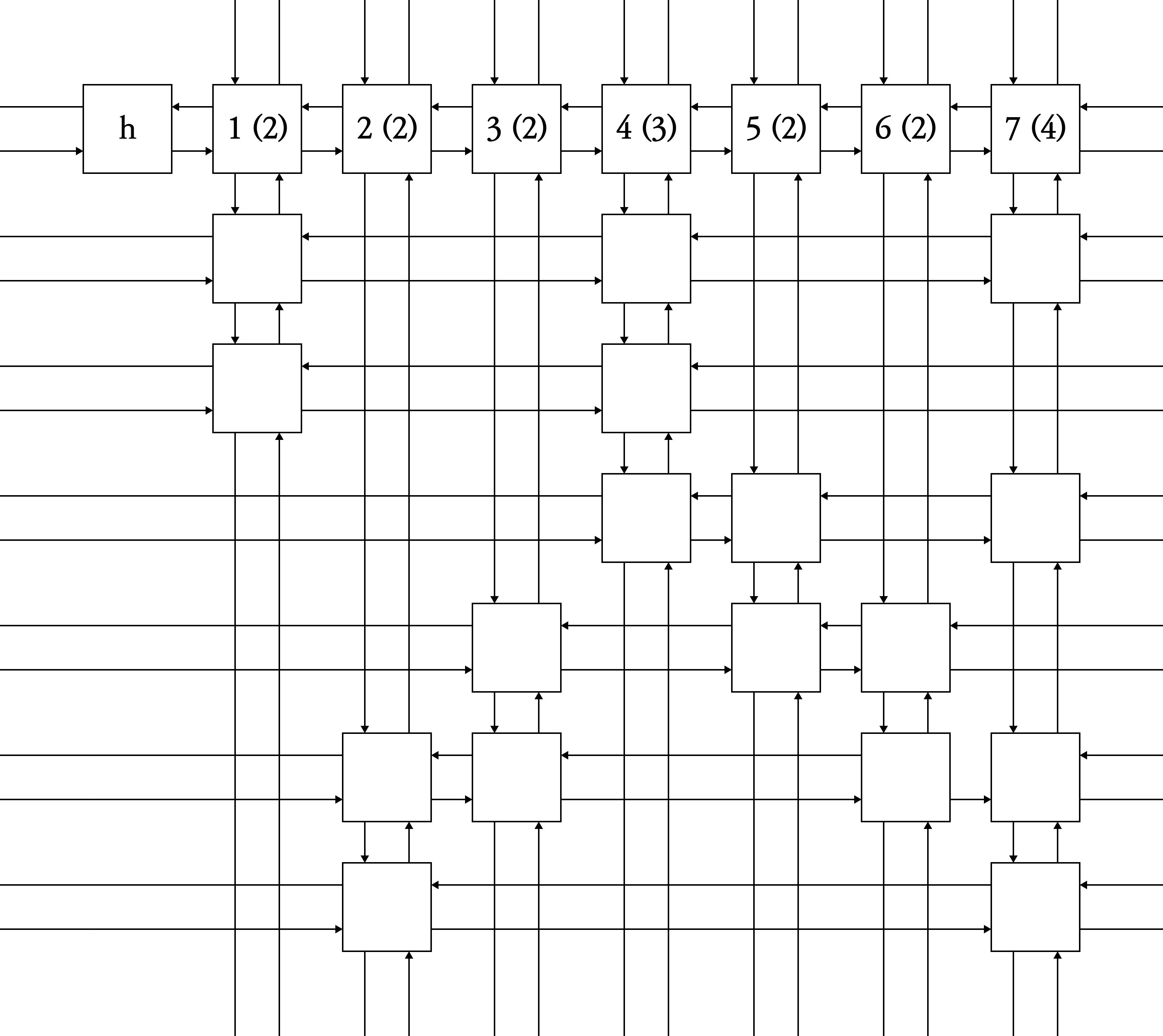
화면 밖에서 들어오거나 나가는 화살표는 반대편 화살표와 이어진다.
"원형" 이중 연결리스트를 상상하면 된다.
DLX - Node
struct node
{
int row; // node의 행 번호
int size; // column의 node 개수
node* col; // column의 head node
node* up;
node* down;
node* left;
node* right;
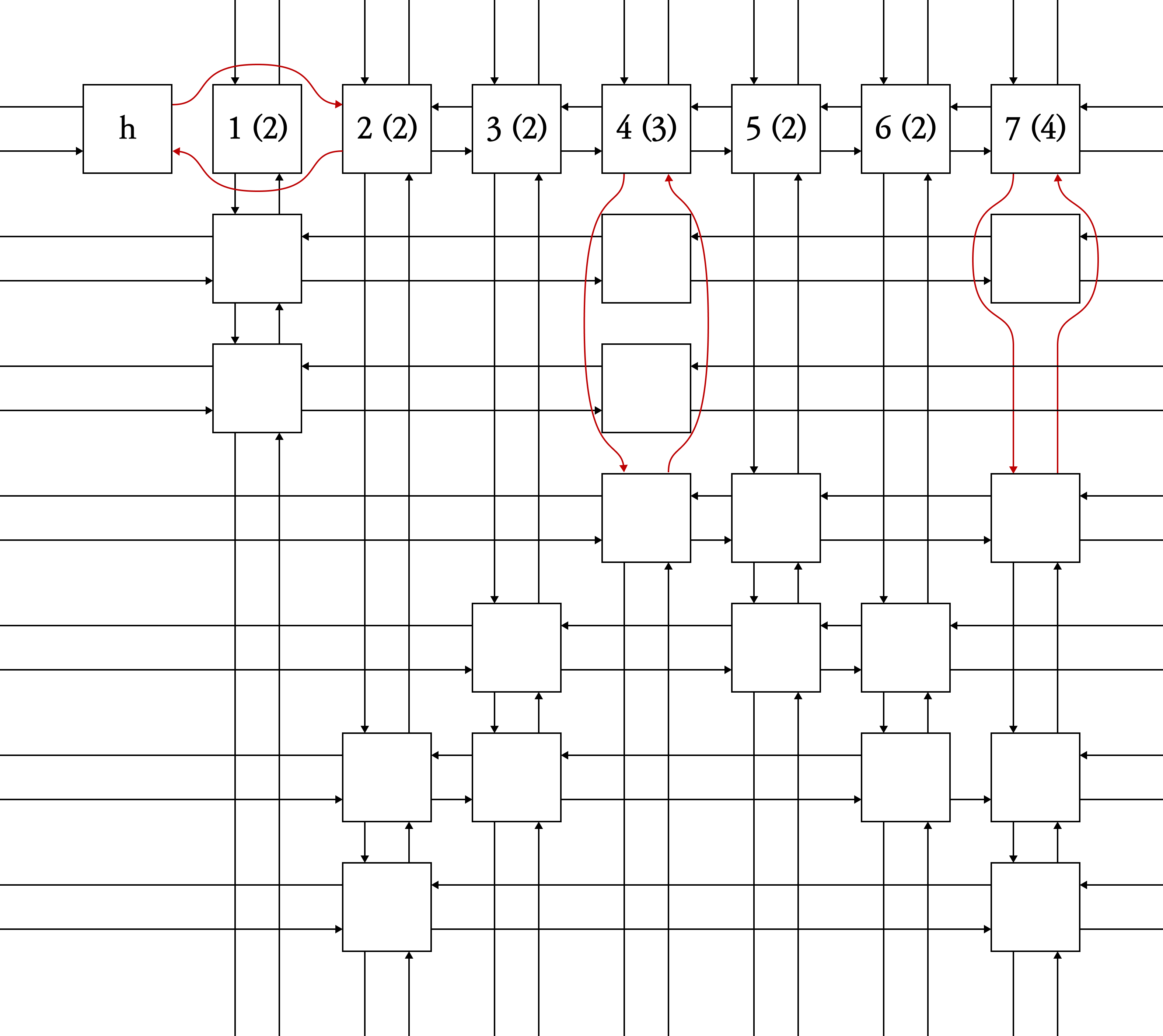
}DLX - Cover
void dlx_cover(node *c) // column head
{
c->right->left = c->left;
c->left->right = c->right;
for (node* it = c->down; it != c; it = it->down) {
for (node* jt = it->right; jt != it; jt = jt->right) {
jt->down->up = jt->up;
jt->up->down = jt->down;
jt->col->size--;
}
}
}
DLX - Uncover
void dlx_uncover(node* c) {
for (node* it = c->up; it != c; it = it->up) {
for (node* jt = it->left; jt != it; jt = jt->left) {
jt->down->up = jt;
jt->up->down = jt;
jt->col->size++;
}
}
c->right->left = c;
c->left->right = c;
}DLX - solve
bool dlx_search(node* head, int k, vector<int>& solution) {
if (head->right == head) return 1;
node* ptr = nullptr;
int low = INF;
for (auto& it = head->right; it != head; it = it->right) {
if (it->size < low) {
if (it->size == 0) return 0;
low = it->size;
ptr = it;
}
}
dlx_cover(ptr);
-
for (auto& it = ptr->down; it != ptr; it = it->down) {
solution.push_back(it->row)
for (auto& jt = it->right; jt != it; jt = jt->right) {
dlx_cover(jt->col);
}
if (dlx_search(head, k + 1, solution)) return 1;
else {
solution.pop_back();
for (node* jt = it->left; jt != it; jt = jt->left) {
dlx_uncover(jt->col);
}
}
}
dlx_uncover(ptr);
return 0;
}DLX와 같이 직접 만든 연결리스트를 사용해야 할 경우 수많은
new가 성능에 매우 큰 영향을 끼친다. 아래와 같이 구현하면 이 비용을 매우 아낄 수 있다.struct node { int row, cnt; node *col, *up, *down, *left, *right; }; node nodes[324 * 729]; node* new_node() { static int idx = 0; return &nodes[idx++]; }
Author's code
19998번 - 스도쿠 (Hard)
문제: https://www.acmicpc.net/problem/19998
풀이: http://boj.kr/699cc393ee0f429e83eb973abe2a4c09
What if...
- 12개의 펜토미노 중 11개만 1번씩 사용해서 50칸을 채우는 문제라면...?
29111번 - Последовательности
문제: https://www.acmicpc.net/problem/29111번역
엑스맨과 센티넬 사이의 결전의 순간이 다가왔다. 교수 X는 이 전투에서 승산이 크지 않다는 것을 알지만, 가능한 모든 기회를 활용하려고 한다.
엑스맨 군대에는 총 명의 전사가 있으며, 교수는 전투력 값 가 부터 까지의 어떤 값이든 해당 전투력을 가진 전사가 정확히 두 명 존재한다는 사실을 알고 있다.전투에서 승리하기 위해 엑스맨은 총 명의 전사를 선택하여 일렬로 서야 한다.
이때 다음 조건을 만족해야 한다:
- 만약 전투력 를 가진 전사 중 한 명이 줄에 포함된다면, 같은 전투력을 가진 다른 전사도 반드시 포함되어야 한다.
- 그리고 두 전투력 전사의 사이에는 정확히 명의 다른 전사들이 있어야 한다.
또한, 전투력 값이 같은 두 전사는 선택되지 않고(=줄에 세우지 않고) 예비대로 남겨두는 경우도 가능하다. 이 예비 인원들은 적절한 순간에 도움을 주기 위해 대기한다.
교수 X가 원하는 이러한 배열을 구성하거나, 그런 배열이 존재하지 않는다면 존재하지 않는다고 말해 주어라.