Trie, Aho-Corasick

Trie

사전지식: 문자열 기초, 재귀

풀고자 하는 문제

이런 상황을 가정해보자.

N개의 정수로 이루어진 집합 A 가 있고, M 개의 쿼리가 주어진다.

쿼리는 다음과 같은 형태다.

exist x: 집합 A에 x가 존재하면 true, 없으면 false

N의 범위가 작다면 Hash Table을 이용하면 되지만, 이런 경우에는 set을 구현할 때 사용되는 BBST(Balanced Binary Tree)를 사용하는 것이 효율적이다.

이 경우, 각 쿼리를 O(log N)에 처리할 수 있다.

이 문제를 문자열로 변형해본다면?

숫자는 두 숫자가 같다는 것을 비교할 때 O(1) 밖에 걸리지 않는다.

그러나 문자열은 최악의 경우, 길이에 비례한 시간이 걸린다. (O(길이))

문자열이 N개 있는 BBST에서는 각 탐색 쿼리가 O(길이 * log N) 이 걸리게 된다.

문자열에 대해서 위와 같은 쿼리를 빠르게 처리하기 위해 Trie 라는 자료구조를 사용한다.

Trie 구조

[“A”, “I”, “IT”, “SUN”, “SUA”, “TO”, “TED”, “TEN”]

이 주어진다고 가정하면 트라이는 다음과 같이 구성된다.

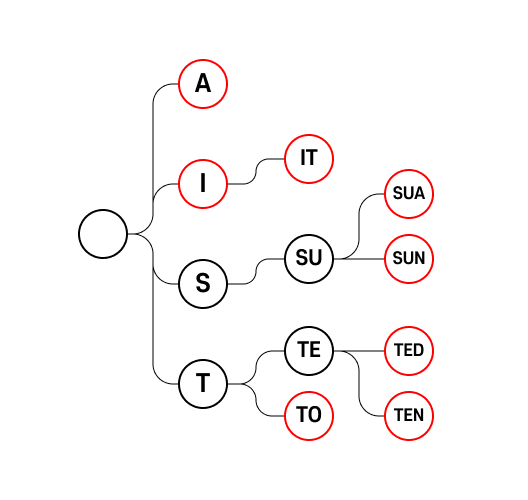
빨간색 정점은 해당 단어가 실제로 존재하는 단어임을 나타낸다.

이를 보통 output link라고 부르는 것 같은 데, 혼란을 주는 이름인 것 같아 이 설명에서는 output check 라고 부르겠다. 코드에서는 valid 변수의 true || false 로 구분하겠다.

검정색 정점은 어떤 다른 단어까지 도달하기 위해 거쳐갈 용도로 생성된 단어임을 나타낸다.

탐색은 루트에서 시작해 찾고자 하는 정점에 갈 때까지 알맞은 간선을 타고 가면 된다.

구현

Node

우선 정점 하나를 나타낼 구조체를 정의해보자.

class Node {
private:
    bool valid;
    int child[26];
public:
    Node() {
    	valid = false;
    	for(int i=0; i<26; i++) child[i] = -1;
    }
friend class Trie;
}

Methods

아마 이런 메서드들이 필요할 것이다.

class Trie {
private:
	vector<Node> trie;
    int _newNode(); // 새로운 정점 생성 및 해당 정점의 인덱스 반환
    void _add(string &str, int node, int idx); // 문자열 삽입
    void _exist(string &str); // 존재하는가?
public:
	Trie(); // 생성자
    void add(string &str);
    bool exist(string &str);
}

하나씩 구현해보자.

_newNode

_newNode 메서드는 Node를 하나 생성해 trie라는 vector에 넣어주고, 인덱스를 반환하면 된다.

int _newNode() {
	Node tmp;
    trie.push_back(tmp);
    return trie.size() - 1;
}

_add

_add 메서드는 재귀적으로 구현된다.

idx는 삽입할 문자열에서 현재 처리하고 있는 인덱스, node는 처리하고 있는 Node의 인덱스이다.

void _add(string &str, int node, int idx) {
	if(idx == str.size()) {
    	trie[node].valid = true;
        return;
    }
    int c = str[idx] - 'A';
    if(trie[node].child[c]) == -1) {
    	int next = _newNode();
        trie[node].child[c] = next;
    }
    _add(str, trie[node].child[c], idx+1);
}

_exist

_exist 메서드는 문자열의 각 문자를 순회하면서 알맞은 간선을 타고 간다.

타고 갈 간선이 없으면 false를 반환하고, 마지막에 도착한 간선의 valid가 false일 때에도 false를 반환한다.

bool _exist(string &str) {
	int now = 0;
    for(int i=0; i<str.size(); i++) {
    	int c = str[i] - 'A';
        if(trie[now].child[c] == -1) return false;
        now = trie[now].child;
    }
    return trie[now].valid;
}

전체 코드

class Node {
private:
    bool valid;
    int child[26];
public:
    Node() {
    	valid = false;
    	for(int i=0; i<26; i++) child[i] = -1;
    }
friend class Trie;
}

class Trie {
private:
	vector<Node> trie;
    int _newNode() {
    	Node tmp;
    	trie.push_back(tmp);
    	return trie.size() - 1;
    }
    void _add(string &str, int node, int idx) {
    	if(idx == str.size()) {
            trie[node].valid = true;
            return;
        }
        int c = str[idx] - 'A';
        if(trie[node].child[c]) == -1) {
            int next = _newNode();
            trie[node].child[c] = next;
        }
        _add(str, trie[node].child[c], idx+1);
    }
    void _exist(string &str) {
    	int now = 0;
        for(int i=0; i<str.size(); i++) {
            int c = str[i] - 'A';
            if(trie[now].child[c] == -1) return false;
            now = trie[now].child;
        }
        return trie[now].valid;
    }
public:
	Trie() {
    	_newNode();
    }
    void add(string &str) {
    	_add(str, 0, 0);
    }
    bool exist(string &str) {
    	return _exist(str);
    }
}

예제

BOJ 5050. 전화번호 목록

문제

전화번호 목록이 주어진다. 이때, 이 목록이 일관성이 있는지 없는지를 구하는 프로그램을 작성하시오.

전화번호 목록이 일관성을 유지하려면, 한 번호가 다른 번호의 접두어인 경우가 없어야 한다.

예를 들어, 전화번호 목록이 아래와 같은 경우를 생각해보자

• 긴급전화: 911
• 상근: 97625999
• 선영: 91125426

이 경우에 선영이에게 전화를 걸 수 있는 방법이 없다. 전화기를 들고 선영이 번호의 처음 세 자리를 누르는 순간 바로 긴급전화가 걸리기 때문이다. 따라서, 이 목록은 일관성이 없는 목록이다.

풀이

일관성이 있는 경우와 없는 경우를 모두 살펴보자.

911
97625999
91125426

이 경우는 일관성이 없다. Trie를 구성해보자.

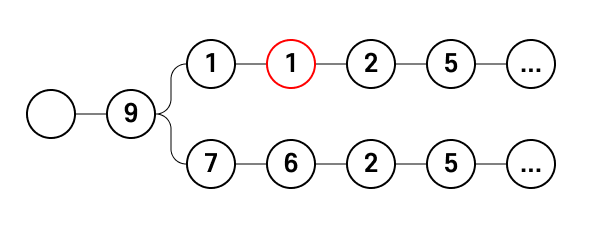
113
12340
123440
12345
98346

이 경우는 일관성이 있다. Trie를 구성해보자.

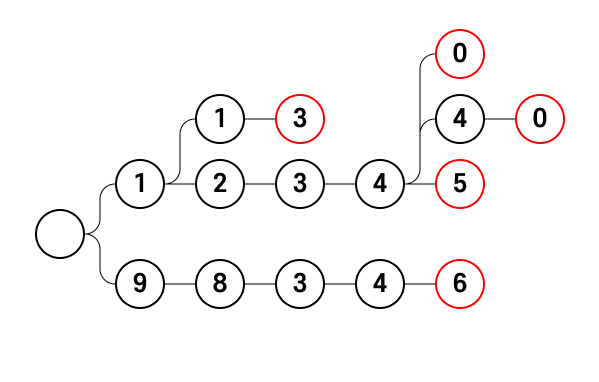
일관성이 있으려면 어떤 문자열이 다른 문자열의 접두사여서는 안된다.

즉, valid한 노드가 무조건 리프노드여야 하는 것이다.

Aho-Corasick Algorithm

사전지식: KMP Algorithm, Trie

Aho-Corasick 알고리즘이란?

Aho-Corasick 알고리즘은 KMP 알고리즘과 거의 흡사하다.

하나의 차이점이 있다면 KMP 알고리즘은 패턴이 한 개일 때 사용한다면, Aho-Corasick 알고리즘은 패턴이 여러개일 때 사용하는 방법이다.

따라서 Aho-Corasick 알고리즘을 한 문장으로 설명하면, KMP에서 사용하는 Failure function을 Trie로 확장시키는 것. 이것이다.

KMP에 대한 설명은 여기에 있다.

시간 복잡도는 $O(|T| + \Sigma|P_i|)$ 이다.

우선 패턴들을 Trie로 나타낸다. 예를 들어 패턴이 ["he", "she", "his", "hers"] 라면 아래처럼 Trie 를 구성할 수 있다.

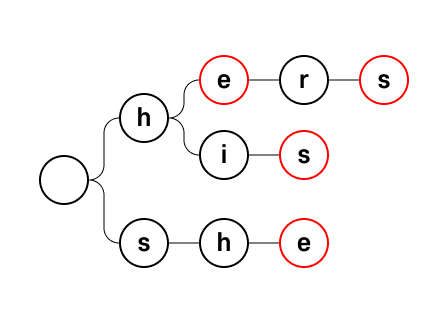
Trie의 각 노드의 Failure function은 다음과 같이 정의된다.

루트가 아닌 각 노드 v에 대해서 루트 -> w로 가는 경로가 루트 -> v로 가는 경로의 접미사이며,
그러한 것들 중 가장 긴 것.

이를 그림으로 나타내면 다음과 같다.

점선이 Failure function을 의미하며, 점선이 없는 노드는 루트를 향한다고 보면 된다.

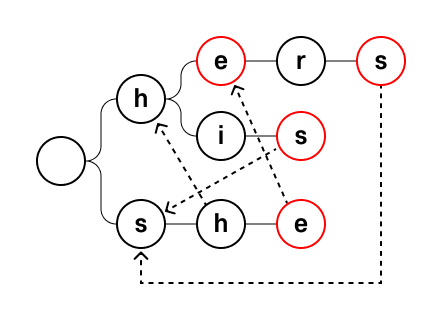
Algorithm

Failure Function을 만드는 이유는 Trie 상의 깊이를 최대로 유지하면서 탐색을 진행하기 위함이다.

끝점을 늘려가면서,

• 만약에 해당 문자열을 포함하는 Trie 상의 경로가 있다면 그곳으로 움직이고
• 그렇지 않다면 Failure Function을 통해서 skip을 반복하는 방식이다.

이를 반복하면 Trie 상의 깊이를 최대로 유지하면서 계속 탐색을 진행할 것이다.

그렇다면 현재 Trie 상의 어떤 노드 v에 있을 때, 루트 -> v로 가는 경로의 substring 중 T에 속한 문자열이 있는 지를 알 수 있을까?

단순하게 생각한다면 Trie의 output check로 판정할 수 있을 것 같지만, Trie상의 깊이를 최대로 유지했기 때문에 그 탐색 중 사이에 문자열이 있다면 이를 찾지 못한다.

이게 무슨말이냐 하면

주어진 문자열에서 패턴 ["OPERATION", "RATIO"]를 찾는다고 가정해보자.

Trie를 구성한다면 다음과 같이 될 것이다.

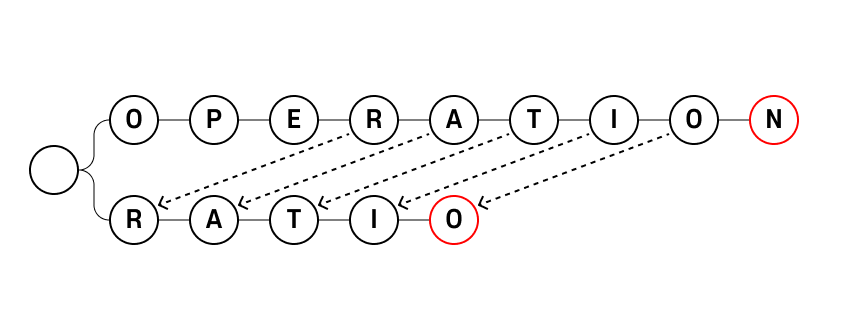
그러면 마지막 N 에 도달했다면, 우리는 중간에 RATIO를 발견할 수 없을 것이다.

이를 Naive하게 해결하는 방법은, 각각의 노드에 도달했을 때마다 Failure function을 타고 올라가면서, 그 중 output check가 있는 노드의 존재를 확인하는 것이다.

이 방법은 전처리를 통해서 시간 복잡도를 줄일 수 있는데, failure function 역시 트리의 형태를 띄므로 failure function tree에서 자식으로 output check를 dfs나 bfs를 통해 뿌려준다면, 각 노드마다 상수 시간에 판정이 가능하다.

Failure Function을 계산하는 방법

Failure function을 계산하는 것은 너비 우선 탐색을 통해서 할 수 있다.

KMP랑 비슷한 방법인데,

• 우선 루트에서의 깊이가 1인 노드들은 failure function이 루트로 자명하다.
• 그 다음, 루트에서의 깊이가 2인 노드들, 깊이가 3인 노드들을 순서대로 탐색한다면, 해당 노드보다 깊이가 낮은 노드들은 이미 다 계산이 완료되었기 때문에 failure function을 계산할 수 있다.
• 이 과정에서 BFS를 사용하기 때문에 한 줄의 코드를 추가하는 것 만으로도 output check를 뿌려줄 수 있게 된다. 고로 위에서 output check를 따로 코딩해야 하는 번거로움이 사라진다.

구현 방법

Trie

우선 Trie 코드부터 시작해보자.

생성자는 vector<string>을 하나 받아서 처리하고 Aho-Corasick에서는 필요없는 메서드들도 삭제하도록 하자.

class Node {
private:
    bool valid;
    int child[26];
public:
    Node() {
    	valid = false;
    	for(int i=0; i<26; i++) child[i] = -1;
    }
friend class Trie;
}

class Trie {
private:
	vector<Node> trie;
    int _newNode() {
    	Node tmp;
    	trie.push_back(tmp);
    	return trie.size() - 1;
    }
    void _add(string &str, int node, int idx) {
    	if(idx == str.size()) {
            trie[node].valid = true;
            return;
        }
        int c = str[idx] - 'A';
        if(trie[node].child[c]) == -1) {
            int next = _newNode();
            trie[node].child[c] = next;
        }
        _add(str, trie[node].child[c], idx+1);
    }
public:
	Trie(vector<string> &v) {
    	_newNode();
        for(auto &x: v) _add(x, 0, 0);
    }
}

Node

노드가 저장해야 하는 정보로는 우선 failure function이 있다. KMP처럼 여기에서도 pi로 저장하자.

class Node {
private:
    bool valid;
    int child[26];
    int pi;
public:
    Node() {
    	valid = false;
    	for(int i=0; i<26; i++) child[i] = -1;
    }
friend class Trie;
}

Failure Function

실패함수는 Trie의 생성자 함수에서 처리해보자.

앞에서 말했듯, BFS로 구현한다.

Trie(vector<string> &v) {
    _newNode();
    for(auto &x: v) _add(x, 0, 0);
    queue<int> q;
    for(auto &x: trie[0].child) {
    	if(x != -1) {
        	q.push(x);
            trie[x].pi = 0;
        } 
    }
    while(!q.empty()) {
    	int f = q.front();
        q.pop();
        for(int i=0; i<26; i++) {
			if(trie[f].child[i] == -1) continue;
            
            int p = trie[f].pi;
            while(p && trie[p][i] != -1) 
            	p = trie[p].pi;
            p = trie[p].child[i];
            
            trie[f].child[i].pi = p;

            if(trie[p].valid)
             	trie[x].child[i].valid = true;

            q.push(child[i]);
            
        }
    }
}

Query

마지막으로 쿼리다. Text를 입력받으면 간단히 패턴이 매칭되었는지 여부만 반환하는 함수를 작성하자.

bool query(string &s) {
	int p = 0;
    for(auto& x: s) {
    	while(p && !trie[p].child[x - 'A'])
        	p = trie[p].pi;
        p = trie[p].child[x-'A'];
        if(trie[p].valid) return 1;
    }
    return 0;
}

전체 코드

Trie 코드와 헷갈리지 않게 이름은 Trie에서 Aho-Corasick으로 바꿔주자.

class Node {
private:
    bool valid;
    int child[26];
    int pi;
public:
    Node() {
    	valid = false;
    	for(int i=0; i<26; i++) child[i] = -1;
    }
friend class AhoCorasick;
}

class AhoCorasick {
private:
	vector<Node> trie;
    int _newNode() {
    	Node tmp;
    	trie.push_back(tmp);
    	return trie.size() - 1;
    }
    void _add(string &str, int node, int idx) {
    	if(idx == str.size()) {
            trie[node].valid = true;
            return;
        }
        int c = str[idx] - 'A';
        if(trie[node].child[c]) == -1) {
            int next = _newNode();
            trie[node].child[c] = next;
        }
        _add(str, trie[node].child[c], idx+1);
    }
public:
	AhoCorasick(vector<string> &v) {
        _newNode();
        for(auto &x: v) _add(x, 0, 0);
        queue<int> q;
        for(auto &x: trie[0].child) {
            if(x != -1) {
                q.push(x);
                trie[x].pi = 0;
            } 
        }
        while(!q.empty()) {
            int f = q.front();
            q.pop();
            for(int i=0; i<26; i++) {
                if(trie[f].child[i] == -1) continue;

                int p = trie[f].pi;
                while(p && trie[p][i] != -1) 
                    p = trie[p].pi;
                p = trie[p].child[i];

                trie[f].child[i].pi = p;

                if(trie[p].valid)
                    trie[x].child[i].valid = true;

                q.push(child[i]);

            }
        }
    }
    
    bool query(string &s) {
        int p = 0;
        for(auto& x: s) {
            while(p && !trie[p].child[x - 'A'])
                p = trie[p].pi;
            p = trie[p].child[x-'A'];
            if(trie[p].valid) return 1;
        }
        return 0;
    }
}

예제

BOJ 9250. 문자열 집합 판별

문제

집합 S는 크기가 N이고, 원소가 문자열인 집합이다. Q개의 문자열이 주어졌을 때, 각 문자열의 부분 문자열이 집합 S에 있는지 판별하는 프로그램을 작성하시오. 문자열의 여러 부분 문자열 중 하나라도 집합 S에 있으면 'YES'를 출력하고, 아무것도 없으면 'NO'를 출력한다.

예를 들어, 집합 S = {"www","woo","jun"} 일 때, "myungwoo"의 부분 문자열인 "woo" 가 집합 S에 있으므로 답은 'YES'이고, "hongjun"의 부분 문자열 "jun"이 집합 S에 있으므로 답은 'YES'이다. 하지만, "dooho"는 모든 부분 문자열이 집합 S에 없기 때문에 답은 'NO'이다.

풀이

이 문제는 Aho-Corasick 알고리즘 그 자체이므로 그냥 구현에만 성공하면 풀 수 있다.