Greedy > 섬 연결하기

그리디라고 보면 그리디지만 그리디 태그를 붙이기엔 너무 양심 없는 문제

MST(Minimum Spanning Tree)

주어진 그래프를 모든 노드를 포함한 트리로 만드는 방법들 중 그 가중치의 합이 가장 적은 트리를 의미한다.

대표적인 MST 구성 알고리즘으로 크루스칼과 프림 알고리즘이 있다.

나는 내 기준으로 구현이 쉬운 프림을 선택했다.

Prim's Algorithm

우선 각 간선을 저장하는 간선 리스트를 구현한다.

만약 아래 그림과 같은 그래프가 주어진다면

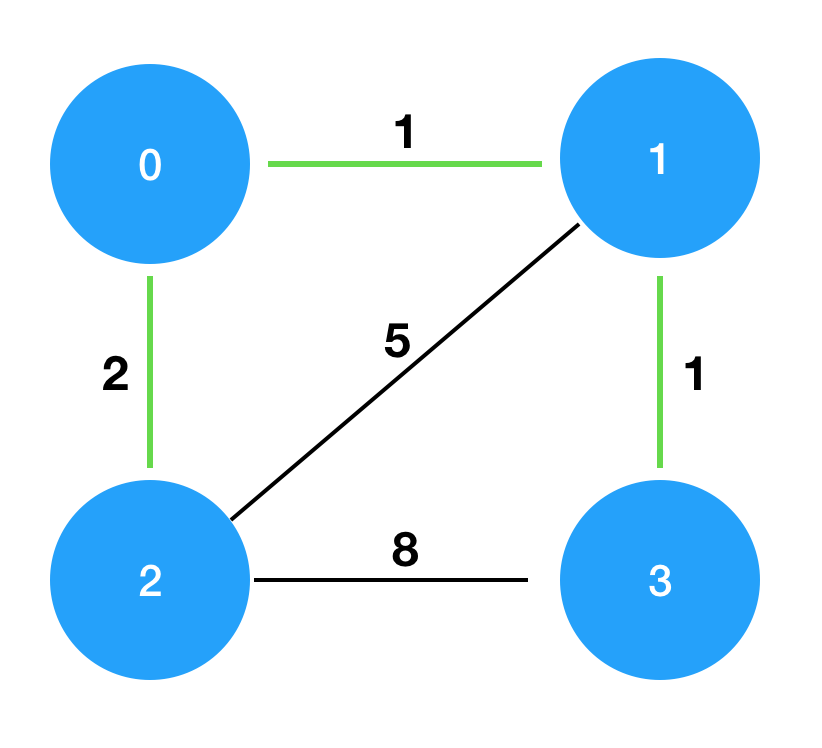
이를 다음과 같은 행렬로 저장할 것이다. {weight, node}

x	edge	edge	edge
0	{1,1}	{2,2}
1	{1,0}	{5,2}	{1,3}
2	{2,0}	{5,1}	{8,3}
3	{1,1}	{8,2}

#include <string>
#include <vector>

using namespace std;

int solution(int n, vector<vector<int>> costs) {
    vector<vector<pair<int, int>>> adj(n);
    for(auto& x: costs) {
        adj[x[0]].push_back({x[2], x[1]});
        adj[x[1]].push_back({x[2], x[0]});
    }   
}

그리고 visited 배열도 만들어 준다.

    vector<int> visited(n);

세 번째로 {weight, node} pair를 넣어줄 최소힙을 만든다.
pair<int,int>가 너무 길기 때문에 축약어를 만들어 준다.

#include <string>
#include <vector>
#include <queue>

using namespace std;

using pii = pair<int,int>

int solution(int n, vector<vector<int>> costs) {
    vector<vector<pii>> adj(n);
    for(auto& x: costs) {
        adj[x[0]].push_back({x[2], x[1]});
        adj[x[1]].push_back({x[2], x[0]});
    }
    vector<int> visited(n);
    priority_queue<pii, vector<pii>, greater<pii>> pq;
    int total_costs = 0;
    
}

그 후 첫 번째 원소를 미리 넣어주자.

    visited[0] = 1;
    for(auto&x: adj[0]) {
        pq.push(x);
    }

이제 프림 알고리즘을 돌리자.

first랑 second도 너무 길기 때문에 F, S로 매크로를 만들자.

    while(!pq.empty()) {
        pii t = pq.top();
        pq.pop();
        if(visited[t.S])
            continue;
        visited[t.S] = 1;
        total_costs += t.F;
        for(auto& x: adj[t.S]) {
            if(!visited[x.S]) {
                pq.push(x);
            }
        }
    }

최종 코드는 다음과 같다.

#include <string>
#include <vector>
#include <queue>

#define F first
#define S second
using namespace std;

using pii = pair<int,int>;

int solution(int n, vector<vector<int>> costs) {
    vector<vector<pii>> adj(n);
    for(auto& x: costs) {
        adj[x[0]].push_back({x[2], x[1]});
        adj[x[1]].push_back({x[2], x[0]});
    }
    vector<int> visited(n);
    priority_queue<pii, vector<pii>, greater<pii>> pq;
    int total_costs = 0;
    
    visited[0] = 1;
    for(auto& x: adj[0]) {
        pq.push(x);
    }
    
    while(!pq.empty()) {
        pii t = pq.top();
        pq.pop();
        if(visited[t.S])
            continue;
        visited[t.S] = 1;
        total_costs += t.F;
        for(auto& x: adj[t.S]) {
            if(!visited[x.S]) {
                pq.push(x);
            }
        }
    }
    
    return total_costs;
}