Relation
- Relation = Table
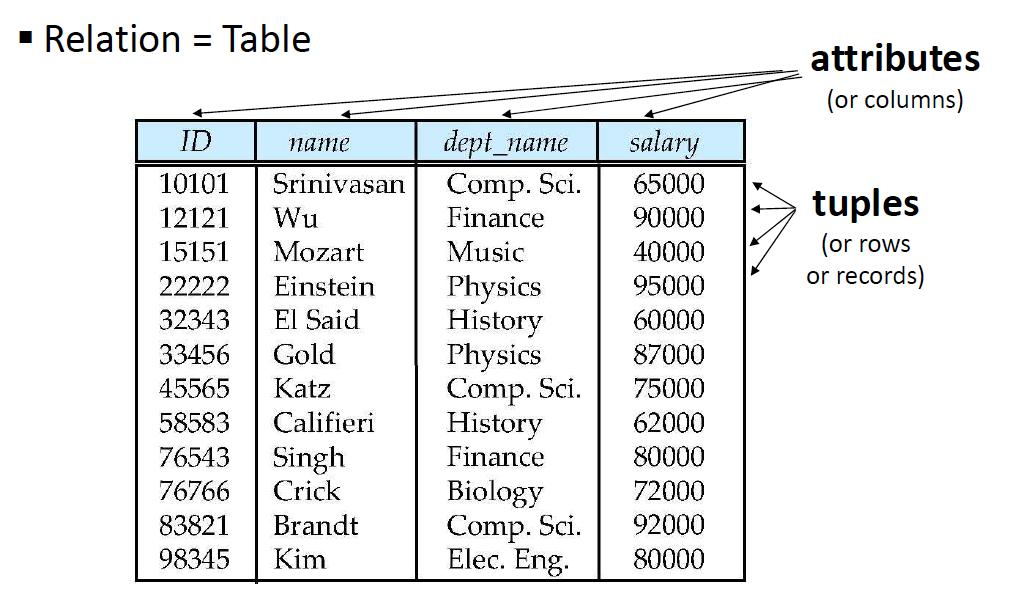
Domain: Attribute types
- 도메인은 각 attribute에 대해 허용된 값들의 집합임
- Domain = data type + constrains
- 예를 들어 Score : 0-100 사이의 숫자
- Attribute 값들은 atomic해야함
- Null은 모든 도메인의 원소임
Relation Schema and Instance
- 이 attributes
- 이 relation schema
- 예를 들어 instructor = (ID, name, dept_name, salary)
- relation은 인스턴스, 즉 tuple들의 집합임.
Relations are Unordered
- tuple들의 순서는 상관없음 (임의의 순서로 저장됨)
- 즉, relation은 집합
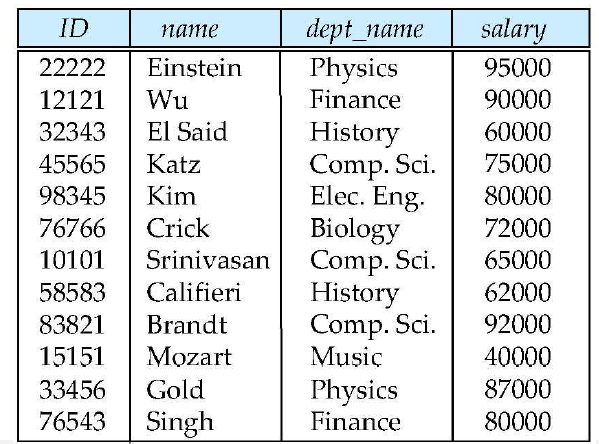
- 즉, relation은 집합
Database
- 데이터베이스는 여러 relation으로 이루어짐
- 예를 들어 대학 데이터베이스는 instructor, student, advisor relation으로 구성됨
Key
- 해당 relation에서 가장 중요한 역할을 수행하는 attribute
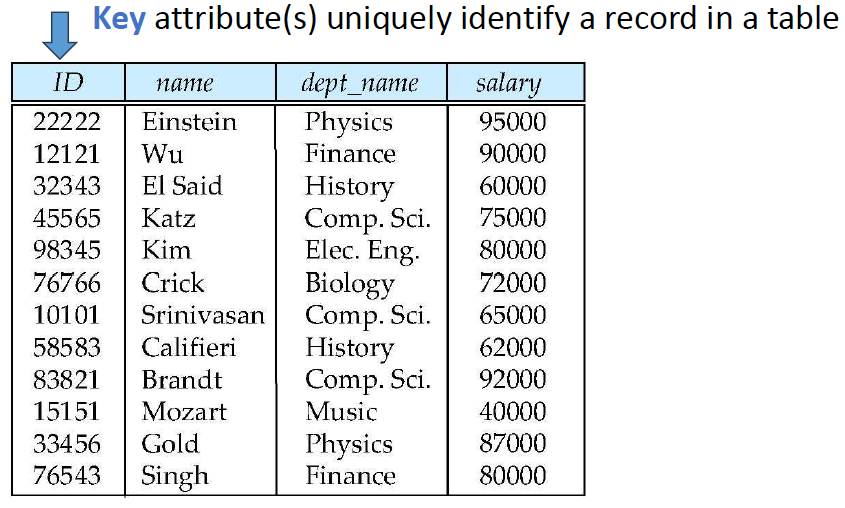
Key의 정의
-
이라 하자
-
만약 의 값들이 relation 의 유일한 순서쌍을 식별하는데 충분하다면, 는 의 superkey임
- 예를 들어 {ID}와 {ID, name}은 모두 instructor의 superkey임
-
Minimal superkey를 candidate key라고 부름
예를 들어 {ID}는 Instructor의 후보키임 -
후보키 중 하나를 primary key로 선택함
Relational Query Languages
두 개의 수학적 query language가 있음
- Relational algebra
- 더 기능적이고, 실행 계획을 나타낼 때 유용함
- Relational calculus
- 더 선언적임. 즉 어떻게 계산할지보다 어떤걸 원하는지를 표현함
- 더 이론적이어서 본 수업에서는 다루지 않음
- 예를 들어 SSN이 10인 학생을 찾는 건
Relational Operators
다섯 개의 기본적인 relational 연산자가 있음
- Union ()
- Selection ()
- Projection ()
- Cartesian Product ()
- Set Difference ()
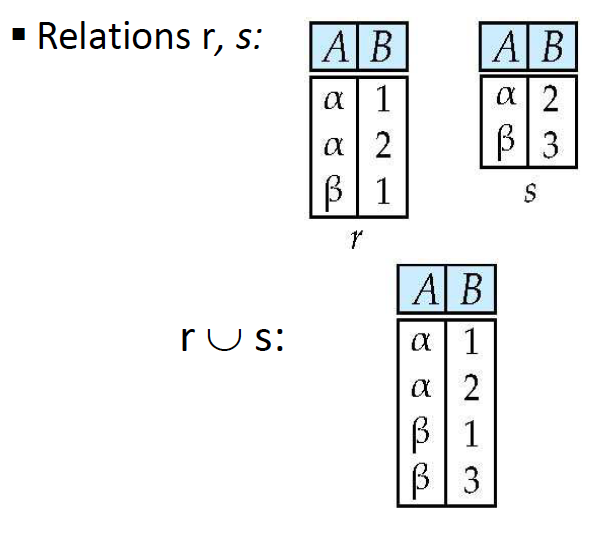
Union ()
합집합
Set difference ()
차집합
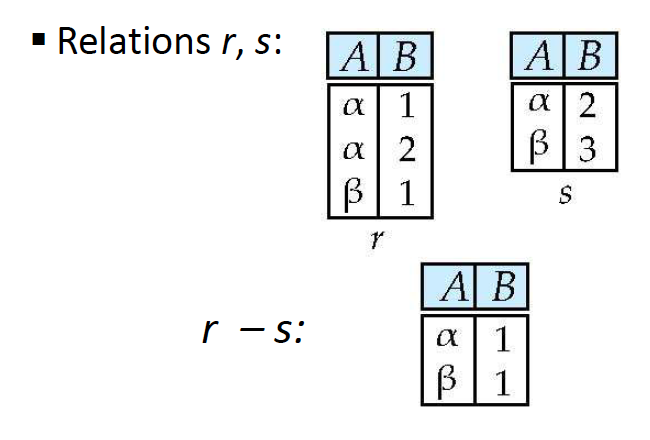
Selection ()
- 행을 선택함
- relation 에 대해서
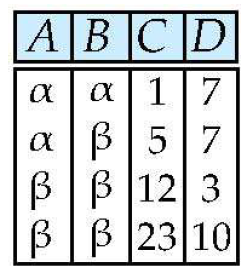
- 여기에서 이고, 인 tuple들을 찾는건 아래와 같이 표현할 수 있음
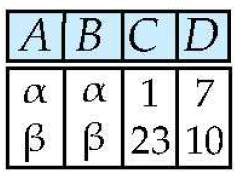
Projection ()
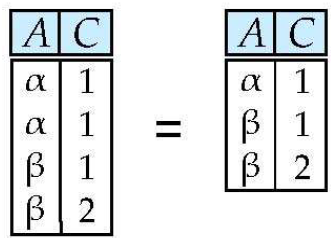
- 프로젝션은 열들을 선택한뒤 중복을 제거함
- 관계 에 대해
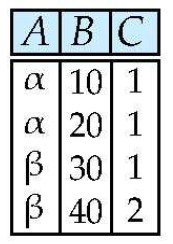
- 와 를 선택하는 Projection 은
Cartesian Product ()
- 카테시안 곱은 가능한 모든 쌍을 생성함
- 관계 에 대해
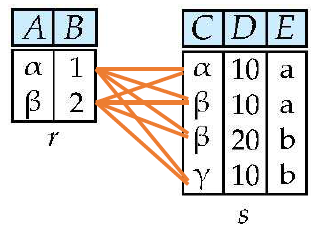

- 중첩루프로도 표현 가능
for each row i in r
for each row j in s
output i,j예시
- 'swe3003'을 듣는 학생들의 이름을 찾아보자

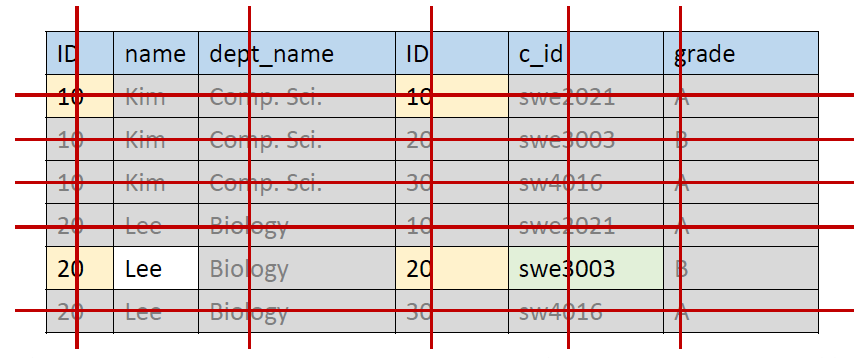
파생연산자
- 기본 5개 관계 연산자만으로 충분하지만,
- Union ()
- Selection ()
- Projection ()
- Cartesian Product ()
- Set Difference ()
- 편의를 위해 파생연산자를 추가함
- Set Intersection ()
- Join ()
- Rename ()
- Division ()
- Group by ()
Set Intersection ()
- 관계 에 대해
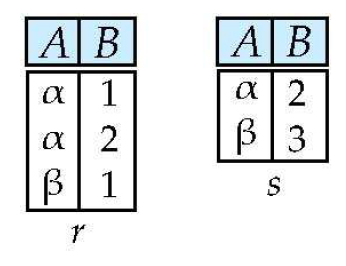
- 교집합 는
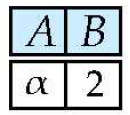
- 이는 가 와 동치이기 때문에 기본연산자가 아님.
Natural Join ()
- 즉 과 의 각 순서쌍 과 에 대해서
- 만약 과 가 같은 attibute를 공유한다면, 과 의 value가 같은 것만 뽑은 뒤 중복을 제거하여 tuple 를 만듦
- 'swe3003'을 듣는 학생들의 이름을 찾아보자
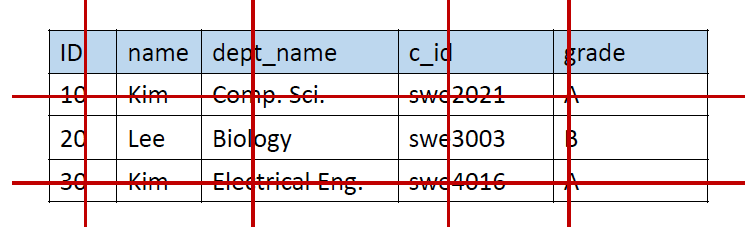
Rename ()
- 같은 테이블이 여러번 사용될 수 있기 때문에 필요함.
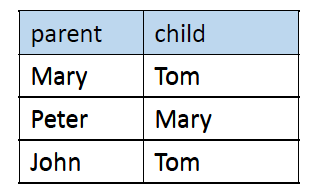
여기에서 Tom의 조부모를 찾기 위해서는, 다음과 같이 할 수 있음
Division ()
- 다음과 같은 쿼리를 표현하는데 유리함
- 모든 CS 과목들을 수강한 학생들을 찾으세요.
- 이 두개의 attributes , 가 를 갖는다면
- 는 들 중 모든 와 매치되는 의 집합을 반환함
- 예를 들어 이 이고, 가 10명 학생의 집합이라면,
- 는 모든 10명과 친구인 모든 들의 집합을 반환함.
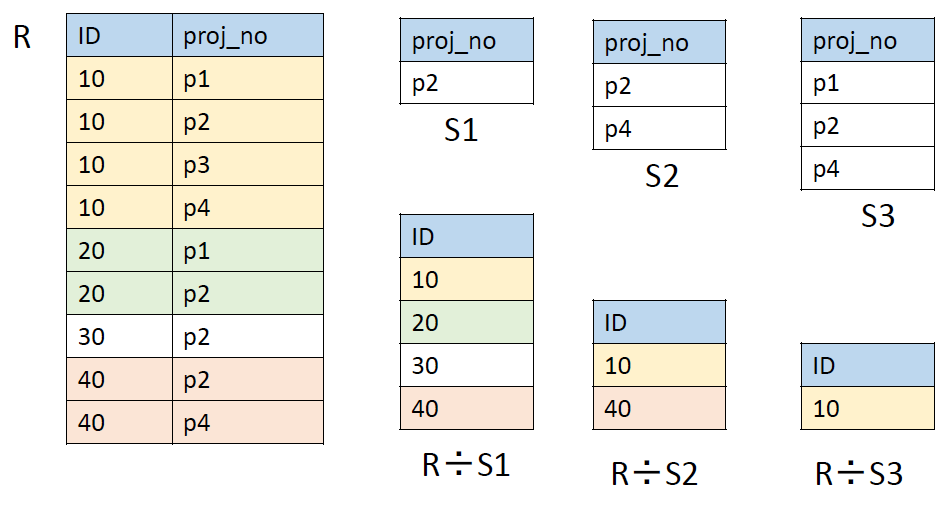
Observations
- Division 는 카테시안 곱의 역임
- 이는 기본 연산자로 표현할 수 있음
