[RL] Model-free Control

On and Off-Policy Learning

On-policy Learning

• 직접 경험을 한다.
• 정책 $\pi$를 통해 얻은 경험으로부터 $\pi$를 학습한다.

Off-policy learning

• 다른 정책 $\pi'$를 통해 얻은 경험으로 부터 $\pi$를 학습한다.

Generalized Policy Iteration with MC Evaluation

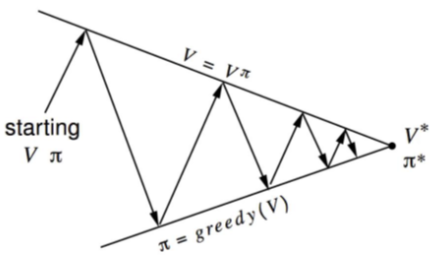
Policy evaluation: Monte-Carlo policy evaluation $V=v_\pi$?
Policy improvement: Greedy?

Model-free Policy Improvement

• $V(s)$를 통한 greedy policy improvement는 MDP의 모델을 필요로 한다.
  $\pi'(s) = \underset{a \in A}{\operatorname{argmax}} \mathcal{R}_s^a + \mathcal{P}_{ss'}^a V(s')$
• 반면 $Q(s,a)$를 통한 greedy policy improvement는 모델이 필요없다.

Generalized POlicy Iteration with Q-Function

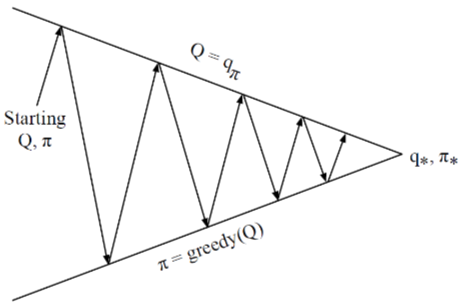
Policy evaluation: Monte-Carlo policy evaluation: $Q=q_\pi$
Policy Improvement: Greedy?

Exploration and Exploitation

Exploration은 환경에 대한 더 많은 정보를 찾는 것을 의미한다.
Exploitation은 이미 알고있는 정보를 이용하여 리워드를 최대화하는 걸 의미한다.

$\epsilon$-Greedy Exploration

이는 exploration을 계속할 수 있는 가장 간단한 아이디어로, 모든 $m$개의 액션들은 0이 아닌 확률로 시도된다.

$\epsilon$-Greedy Improvement

Theorem: 어떤 $\epsilon$-greedy 정책 $\pi$에 대해서 $q_\pi$에 대한 $\epsilon$-greedy 정책 $\pi'$는 다음을 만족한다.

$v_{\pi'}(s) \ge v_\pi(s)$

Monte-Carlo Policy Iteration

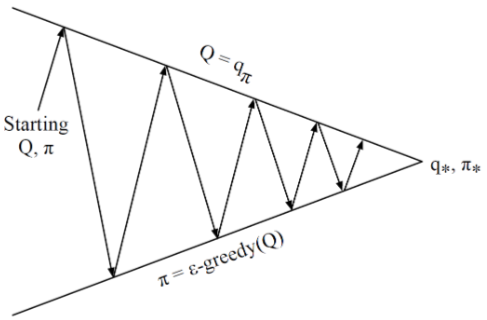
Policy evaluation: Monte-Carlo policy evaluation: $Q=q_\pi$
Policy Improvement: $\epsilon$-Greedy policy improvement

Variant Monte-Carlo Policy Iteration

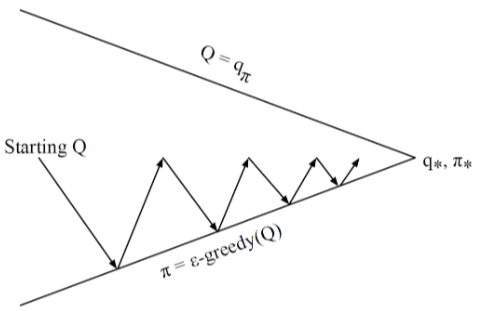
매 에피소드마다:

Policy evaluation: Monte-Carlo policy evaluation: $Q\approx q_\pi$
Policy Improvement: $\epsilon$-Greedy policy improvement

Greedy in the Limit with Infinite Exploration (GLIE)

Definition: GLIE
모든 state-actionh 순서쌍은 무한히 많이 탐험될 수 있어야 한다.

$\lim_{k \to \infty} N_k(s, a) = \infty$

policy는 결국 greedy policy로 수렴해야 한다.

$\lim_{k \to \infty} \pi_k(a|s) = \mathbf{1}\left(a = \underset{a' \in \mathcal{A}}{\operatorname{argmax}} Q_k(s, a')\right)$

예를 들어 $\epsilon_k = \frac 1 k$라면 GLIE이다.

Monte-Carlo Control

$k$번째 에피소드를 샘플링함 $\pi : \{S_1,A_1,R_2, \dots, S_T\}\sim \pi$

각 상태 $S_t$와 행동 $A_t$에 대해서

그리고 새로운 action-value function을 기반으로 정책을 업데이트한다.

MC vs TD control

TD는 MC보다 다음과 같은 장점들이 있다.

• 낮은 variance
• online
• 완료되지 않은 시퀀스

자연스러운 생각은 MC대신 바로 TD를 적용하는 것이다.

• TD를 $Q(S,A)$에 적용하고,
• $\epsilon$-greedy로 정책을 improve하고
• 매 타임스텝마다 업데이트

Model-free Policy Iteration with TD Methods

• Policy evaluation $Q_\pi$를 매 time-step마다 temporal difference를 이용해서 학습
• Policy improvement: MC와 동일하게 $\epsilon$-greedy

Updating Action-Value Functions with SARSA

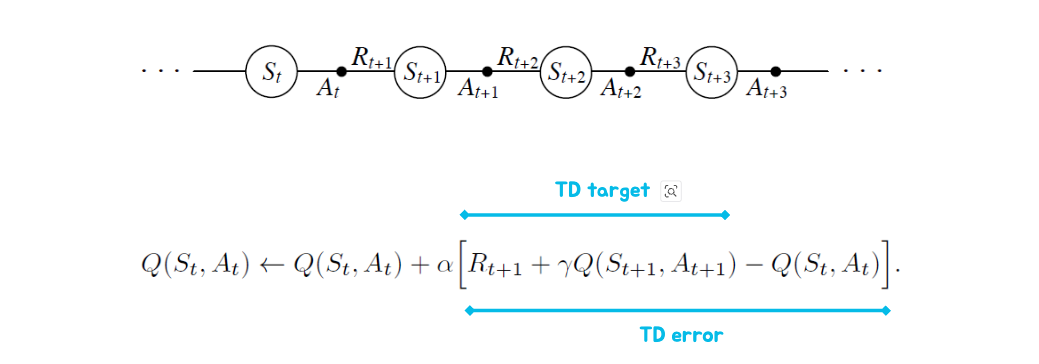
Policy Control with SARSA

• 매 time-step마다
  • policy evaluation: $Q(S,A) \larr Q(S,A) + \alpha(R + \gamma Q(S',A') - Q(S,A)$
  • policy improvement: $\epsilon$-greedy

SARSA

n-step SARSA

Off-Policy Learning

정책 $\mu(a|s)$를 따를 때, $v_\pi(s)$나 $q_\pi(s,a)$를 계산하여 $\pi(a|s)$를 평가할 수 있을까?

Importance Sampling

• 다른 분포의 기댓값을 추정하는 방법

Importance Sampling for Off-Policy Monte-Carlo

• $\pi$를 계산하기 위해 $\mu$로부터 생성된 return을 사용
• return $G_t$를 두 정책의 유사도에 따라 가중해야함
• 전체 에피소드에 대한 imporance weight를 곱해줌
  $G_t^{\pi/\mu} = \frac{\pi(A_t|S_t)}{\mu(A_t|S_t)} \frac{\pi(A_{t+1}|S_{t+1})}{\mu(A_{t+1}|S_{t+1})} \cdots \frac{\pi(A_T|S_T)}{\mu(A_T|S_T)} G_t$
• 수정된 return을 통해 value를 업데이트함.
  $V(S_t) \leftarrow V(S_t) + \alpha \left( G_t^{\pi / \mu} - V(S_t) \right)$
• 단 $\mu$가 0이면 사용할 수 없고, 이는 매우 variance를 크게 만들 수 있음

Importance Sampling for Off-Policy TD

• TD target $R_{t+1} + \gamma V(S_{t+1})$에 importance sampling을 적용함.
  $V(S_t) \leftarrow V(S_t) + \alpha \left( \frac{\pi(S_t, A_t)}{\mu(S_t, A_t)} \right) (R_{t+1} + \gamma V(S_{t+1}) - V(S_t))$
• 이는 MC importance sampling보다 훨씬 variance가 작음

Q-Learning: Off-policy TD Control

• 이제 action-value $Q(S,A)$에 대해 생각해보자.
• imporance sampling은 필요없다.
• 다음 action은 $A_{t+1} \sim \mu(S_t)$에 의해 뽑힌다.
• 그러나 우리는 다른 후속 action $A' \sim \pi(S_t)$를 려해야한다.
• 그리고 $Q(S_t,A_t)$를 대책 action의 value로 업데이트한다.

$Q(S_t,A_t) \larr Q(S_t,A_t) + \alpha(R_{t+1} + \gamma Q(S_{t+1},A') - Q(S_t,A_t))$

target policy $\pi$를 greedy하게 잡으면

그러면 Q-learning 타겟이 다음과 같이 간단해진다.

SARSA vs Q-Learning

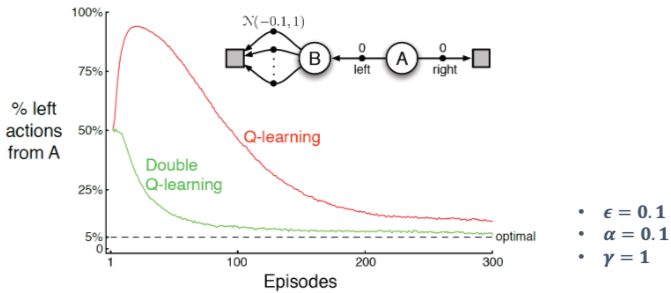
Maximization Bias

1. 하나의 상태(state)만 있는 MDP(Markov Decision Process)를 가정하고, 가능한 두 가지 행동 $a_1$, $a_2$가 있다고 하자.
2. 이 두 행동은 모두 평균이 0인 확률적 보상(reward)을 가진다:
   $\mathbb{E}(r \mid a = a_1) = \mathbb{E}(r \mid a = a_2) = 0$
3. 기대 보상이 0이므로, 이론적인 Q값도 둘 다 0이다:
   $Q(s, a_1) = Q(s, a_2) = 0$
4. 이전에 a_1과 a_2를 각각 실행해 본 샘플들이 존재한다고 가정하자. (즉, 학습 데이터가 있음)
5. 이는 실제 Q가 아니라 샘플 기반으로 추정한 Q값이다. 즉, 유한한 샘플로부터 계산된 Q값:
   $\hat{Q}(s, a_1),\quad \hat{Q}(s, a_2)$
6. 추정된 Q값을 기반으로, greedy 정책 \hat{\pi}를 정의한다. 즉, 가장 높은 \hat{Q}를 선택하는 정책:
   $\hat{\pi} = \arg\max_{a’} \hat{Q}(s, a’)$
7. 샘플로 계산한 추정값 중 최댓값을 취하면, 평균은 0이더라도 양수가 될 가능성이 높다.
   → 최대화 편향(Maximization Bias) 발생:
   $\mathbb{E}\left[\max\left(\hat{Q}(s, a_1),\ \hat{Q}(s, a_2)\right)\right] > 0$

Double Learning

• Q값에 대한 greedy policy는 최대화 편향을 발생시킬 수 있다.
• 이를 보완하기 위해 두개의 $Q_1$, $Q_2$를 둔다.
  • 하나의 추정치를 통해 max action을 선택함: $a^* = \argmax_a Q_1(s,a)$
  • 다른 Qㄹ를 이용해서 value를 계산함 $a^*: Q_2(s,a*)$