[RL] Model-free Prediction

Review

Return은 step $t$에서 총 할인된 리워드들의 합이다.

$v_\pi(s)$는 $s$ 상태에서 $\pi$ 정책하에 return의 기댓값이다.

$q_\pi(s,a)$는 $s$ 상태에서 $a$행동을 했을 때, $\pi$ 정책하에 return의 기댓값이다.

Model-free Reinforcement learning

Model-free prediction(evaluation)

• MDP를 모를 때 value function을 예측하는 것
• 이 policy가 얼마나 좋은지

Model-free control(improvement)

• MDP를 모를 때 value function을 최적화하는 것
• 어떻게 더 좋은 policy를 학습할 수 있을지

Model-free Policy Evaluation

• 실제 MDP 모델 없이 특정 policy의 기대 return 값을 예측하는 것.

Monte-Carlo Reinforcement Learning

• MC method는 경험들의 episode로 직접 학습한다.
• MC는 model-free로, MDP transition이나 reward에 대한 지식이 필요없다.
• MC는 완전한 episode를 통해 학습한다: Bootstapping을 하지 않는다.
• MC는 간단한 아이디어를 사용한다: value가 return의 평균이라는 것.
• episodic MDP에서만 적용할 수 있다. 즉: 모든 에피소드는 종료되어야 한다.

Monte Carlo Policy Evaluation

• 목표: $\pi$ 하의 경험들의 episode로 $v_\pi(s)$를 학습하는 것.
  $S_1, A_1, R_2, \dots, S_k \sim \pi$
• return은 총 discounted reward임
  $G_t = R_{t+1} + \gamma R_{t+2} + \cdots + \gamma^{T-1} R_T$
• value function은 expected return임
  $V_\pi(s) = \mathbb{E}_\pi[G_t | S_t = s]$
• Monte-Carlo policy evaluation은 expected return 대신 경험적 mean return을 사용함.

First-Visit Monte-Carlo Policy Evaluation

State $s$를 평가하기 위해

• 에피소드에서 $s$에 처음 도달한 시간 $t$에,
• counter를 증가시키고 $N(s) \larr N(s) + 1$
• total return을 증가시키고, $S(s) \larr S(s) + G(t)$
• value를 mean return으로 업데이트하고 $V(s) \larr \frac {S(s)}{N(s)}$
• 큰수의 법칙에 따라 $N(s)\rarr \infin$에 따라 $V(s)\rarr V_\pi(s)$로 수렴한다.

Every-Visit Monte-Carlo Policy Evaluation

State $s$를 평가하기 위해

• 에피소드에서 $s$에 매번 도달한 시간 $t$에,
• counter를 증가시키고 $N(s) \larr N(s) + 1$
• total return을 증가시키고, $S(s) \larr S(s) + G(t)$
• value를 mean return으로 업데이트하고 $V(s) \larr \frac {S(s)}{N(s)}$
• 큰수의 법칙에 따라 $N(s)\rarr \infin$에 따라 $V(s)\rarr V_\pi(s)$로 수렴한다.

Incremental Mean

Incremental Monte-Carlo Update

각 state마다, 리턴 $G_t$로 상태 $S_t$를 업데이트할 수 있다.

non-stationary problem에서는 다음과 같이 running mean을 계산할 수 있다.

Temporal-Difference Learning

• TD도 똑같이 경험의 epidsode를 통해 직접 학습한다.
• TD도 model-free로, MDP transition이나 reward에 대한 사전지식 없이 학습할 수 있다.
• TD는 완료되지 않은 episode에 대해 학습할 수 있다.
• TD는 예측값을 예측값을 통해 업데이트한다. (bootstrapping)

Monte Carlo vs Temporal Difference

Incremental Monte-Carlo:

Temporal-difference elarning algorithm

• value $V(S_t)$를 $R_{t+1} + \gamma V(S_{t+1})$로 업데이트한다.
  $V(S_t) \leftarrow V(S_t) + \alpha (R_{t+1} + \gamma V(S_{t+1}) - V(S_t))$
• $R_{t+1} + \gamma V(S_{t+1})$를 TD target이라고 부르고, $\delta_t = R_{t+1} + \gamma V(S_{t+1}) - V(S_t)$를 TD error라고 부른다.

MC vs TD

MC는 완전한 시퀀스로부터만 학습할 수 있다.

• MC는 에피소드의 끝까지 기다려야 한다.
• MC는 episodic 환경에서만 동작한다.

TD는 완료되지 않은 시퀀스로부터 학습할 수 있다.

• TD는 최종 outcome 없이 학습할 수 있다.
• TD는 매 스텝마다 온라인으로 학습할 수 있다.
• TD는 continuing 환경에서도 동작한다.

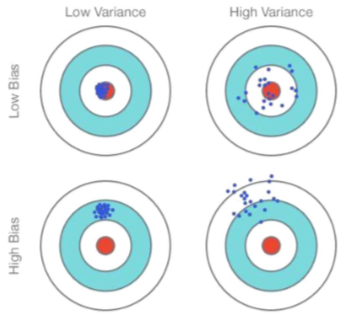
Bias/Variance Trade-off

• bias는 학습 알고리즘에서 잘못된 가정으로부터 도출된 에러임.
• variance는 training set에서 작은 변동으로 인한 민감도로 부터 나오는 에러임.

• return $G_t = R_{t+1} + \gamma R_{t+2} + \dots$는 $v_\pi(s_t)$의 unbiased 추정이다.
• 실제 TD target은 $v_\pi(s_t)$의 unbiased 추정이다.
• 그러나 TD target $R_{t+1} + \gamma V(S_{t+1})$은 biased 추정이다.
• TD target은 return보다 훨씬 낮은 variance를 갖는다.

Bias/Variance of MC vs TD

MC: high variance, zero bias
TD: low variance, some bias

Batch MC and TD

Finite dataset에 대한 batch(offline) solution

• 주어진 $K$개의 episode에 대해
• 반복적으로 $k \in [1,K]$를 샘플링해서
• 샘플링된 에피소드에 대해 MC나 TD를 적용

MC vs TD

• 가장 단순한 TD에서 $(s,a,r,s')$를 $V(s)$를 업데이트할때 사용한다.
• 따라서 업데이트당 $O(1)$, 에피소드 당 $O(L)$이 소요
• MC 도 에피소드 당 $O(L)$이 소요됨.
• TD는 Markov structure를 이용하므로, Markov 도메인에서 유용하다.
• MC는 Markov property를 이용하지 않으므로, non-Markov 환경에서 더 유용하다.

n-step Return

n-step temporal-difference learning은 다음과 같이 할 수 있다.

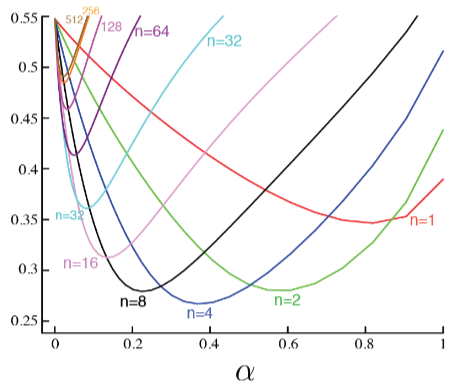
Averaging n-step Returns

여러 $n$에 대해서 $n$-step return을 평균할 수 있다. 예를 들어:

모든 time-step의 정보를 효율적으로 모을 수 있을까?

$\lambda$-return

TD($\lambda$)는 $n$-step update를 평균하는 하나의방법으로,

• 각각은 $\lambda^{n-1}$의 비율로 가중되며,
• $\lambda$-return은 다음과 같이 정의된다.
  $G_t^\lambda \doteq (1 - \lambda) \sum_{n=1}^{\infty} \lambda^{n-1} G_{t:t+n}$
• 그리고 이 $\lambda$-return을 이용한 백업은 다음과 같다.
  $V(s_t) = V(s_t) + \alpha[G_t^\lambda - V_t(s_t)]$

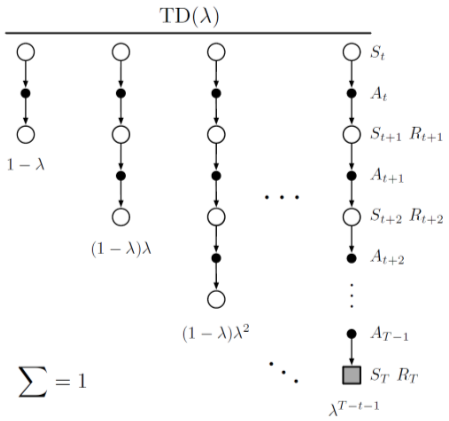
$\lambda$가 0이면 one-step TD를 하는 것이고,
$\lambda$가 1이면 MC를 하는 것이다.